不等式的简单变形

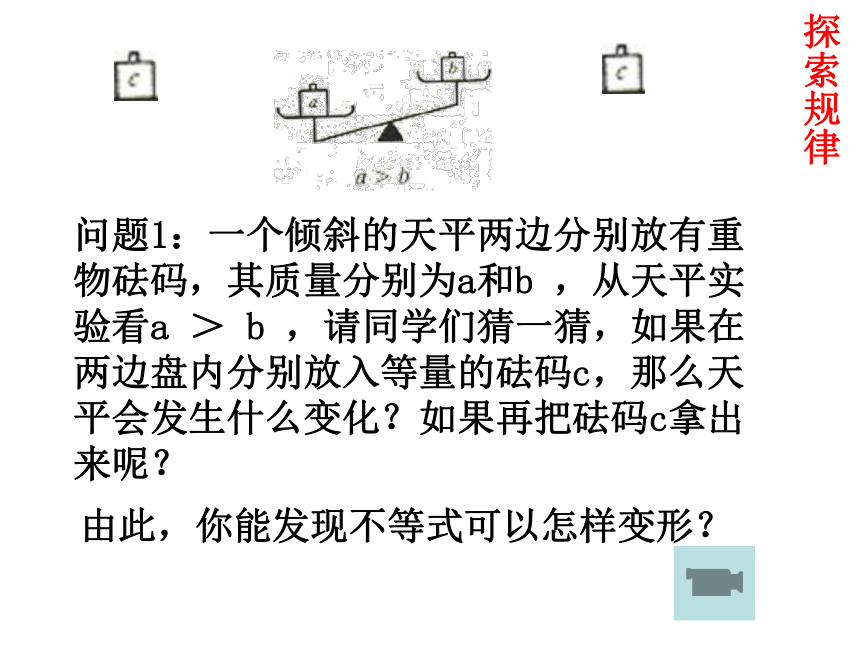
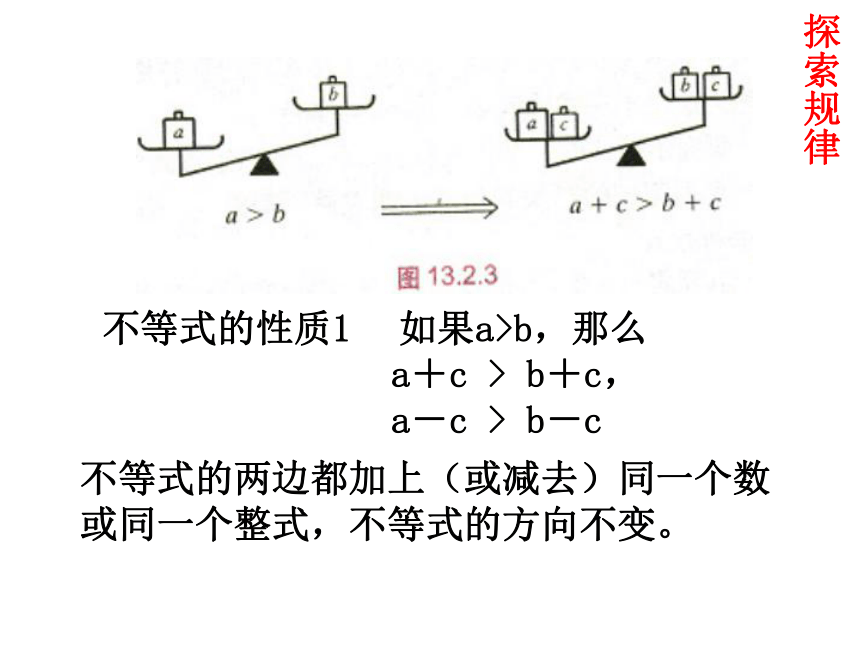
课件17张PPT。Welcome to our class不等式的简单变形问题1：一个倾斜的天平两边分别放有重物砝码，其质量分别为a和b ，从天平实验看a ＞ b ，请同学们猜一猜，如果在两边盘内分别放入等量的砝码c，那么天平会发生什么变化？如果再把砝码c拿出来呢？探索规律由此，你能发现不等式可以怎样变形？不等式的性质1 如果a>b，那么
a＋c > b＋c，
a－c > b－c 不等式的两边都加上（或减去）同一个数或同一个整式，不等式的方向不变。 探索规律　尝试探索例1：解不等式：
（1）x－7<8 （2）3x<2x-3这两小题中不等式的变形与方程的什么变形相类似？ 解： 两边都加上7得，不等号方向不变
解：两边都减去2x，
不等号方向不变得 x-7+7 <8+7
3x-2x <2x-3-2x
移x <8+7x <153x-2x <-3x <-3这里的变形与方程中的移项相类似：注意：移项要变号移例1：解不等式（1）X－7＜8（2）3X＜2X －3解：不等式的两边都加上7，不等式的方向不变，所以
　 　
　

举例分析＋7＋7解：不等式的两边都减去2x（即加上－2x）,不等号的方向不变,所以
－2x －2x x<8+7x<153x－2x ＜ －3得 x ＜ －3x－7 <8 3x ＜2x－3
注意：不等式的移项要变号随堂练习：
解下列不等式，并在数轴上表示出它们的解集： 不等式的两边都乘以（或除以）同
一个不等于0的数，不等号的方向是否也
不变呢 ？探索规律试一试！ 将不等式7 ＞4两边都乘以同一个数，比较所得的数的大小，用“＜”或“＞”填空：从中你能发现什么？ ＞不变＞不变＞不变=变＜＜＜变变变不等式的性质2 如果a＞b，并且c＞0，
那么ac＞bc
不等式的性质3 如果a＞b，并且c＜0，
那么ac＜bc不等式两边都乘以（或除以）同一个正数，不等号的方向不变；不等式两边都乘以（或除以）同一个负数，不等号的方向改变。 解：不等式的两边都乘以2，
不等号的方向不变，
所以：
解：不等式的两边都除以-2
，不等号的方向改变，所以
x > -6(2) –2x < 6 –2x ÷（-2） 6 ÷（-2） x > -3这两小题中不等式的变形与方程的什么变形有什么不同？这两小题中不等式的变形与方程的什么变形相类似？将未知数的系数化为1，即化为 x>a或x>随堂练习：解下列不等式，并把解集在数轴上表示出来：练习、已知x ＞ y，用＜或＞填空
（1）x-6 y-6
(2)
(3) -2x -2y
（4） x+9 y+9
（5）2x+1 2y+1
（6）-3x-1 -3y-1
＞＜＜＞＞＞填一填?
不等式与方程的性质比较
方程两边加上（减去）同一个数成同一个整式，方程仍成立
方程两边都乘以（或除以）同一个正数，方程仍成立
不等式的两边加上（或减去）同一个数或同一个整式，不等号的方向不变
个正数不等式的两边都乘以（或除以）同一，不等号的方向不变
不等式的两边都乘以（或除以）同一个负数，不等号的方向改变
(1)由 x＞y 得 ax＞ay 的条件是（ ）
A.a＞0 B.a＜0 C.a≥0 D.a≤0
(2)由 x＞y 得 ax≤ay 的条件是（ ）
A.a＞0 B.a＜0 C.a≥0 D.a≤0
(3)若 a＞1，则下列各式中错误的是（ ）
A.4a＞4 B.a+5＞6 C. ＜ D.a-1＜0ADD看谁做得好！不等式的性质课堂聚焦加减类似解方程，
乘除运用要思考：
若是正数还如故，
唯有负数才变号。请你大胆地试一试：a是一个整数，你能确定a与3a的大小吗？当a＞0时， a＜3a；
当a＝0时， a＝ 3a；
当a＜0时， a＞3a。解下列不等式，并在数轴上表示出来：
1、X－2>0 2、X＋1>0
3、－2x<4 4、3x+3≤0
解：x >2x >-1x >-2x ≤-1