2024年中考数学专项提升练习:旋转(含简单答案)
文档属性
| 名称 | 2024年中考数学专项提升练习:旋转(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 716.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-08 00:00:00 | ||
图片预览



文档简介
2024年中考数学专项提升练习:旋转
一、单选题
1.在第四象限内有一点,且,那么点M关于原点对称的点的坐标是( )
A. B. C. D.
2.2023年10月26日,神州十七号载人飞船发射任务圆满成功.下列航天图标是中心对称图形的是( )
B.
C. D.
3.如图,把绕点顺时针旋转某个角度后得到,若,,则旋转角等于( )
A. B. C. D.
4.如图,把绕着点A顺时针方向旋转,得到,点C刚好落在边上.则( )
A. B. C. D.
5.如图,直线l是正方形的一条对称轴,l与,分别交于点M,N.,的延长线相交于点P,连接.下列三角形中,与成中心对称的是( )
A. B. C. D.
6.某个正六边形螺帽需要拧4圈才能拧紧,小梧用扳手的卡口卡住螺帽,通过转动扳手的手柄来转动螺帽(如图所示).以此方式把这个螺帽拧紧,他一共需要转动扳手的次数是( )
A.4 B.16 C.24 D.32
7.中,,将绕点O顺时针旋转,点A的对应点记为C,点B的对应点记为D,顺次连接得到四边形.所得到的四边形为( )
A.梯形 B.矩形 C.菱形 D.正方形
8.如图,在正方形中,,E为边上一点,点F在边上,且,将点E绕着点F顺时针旋转得到点G,连接,则的长的最小值为( )
A.3 B.2.5 C.4 D.
二、填空题
9.若点与点关于原点对称,则 .
10.如图,在中,,,将绕点顺时针旋转得到,其中点与点是对应点,点点是对应点,若点恰好落在边上,则旋转角的大小为 °.
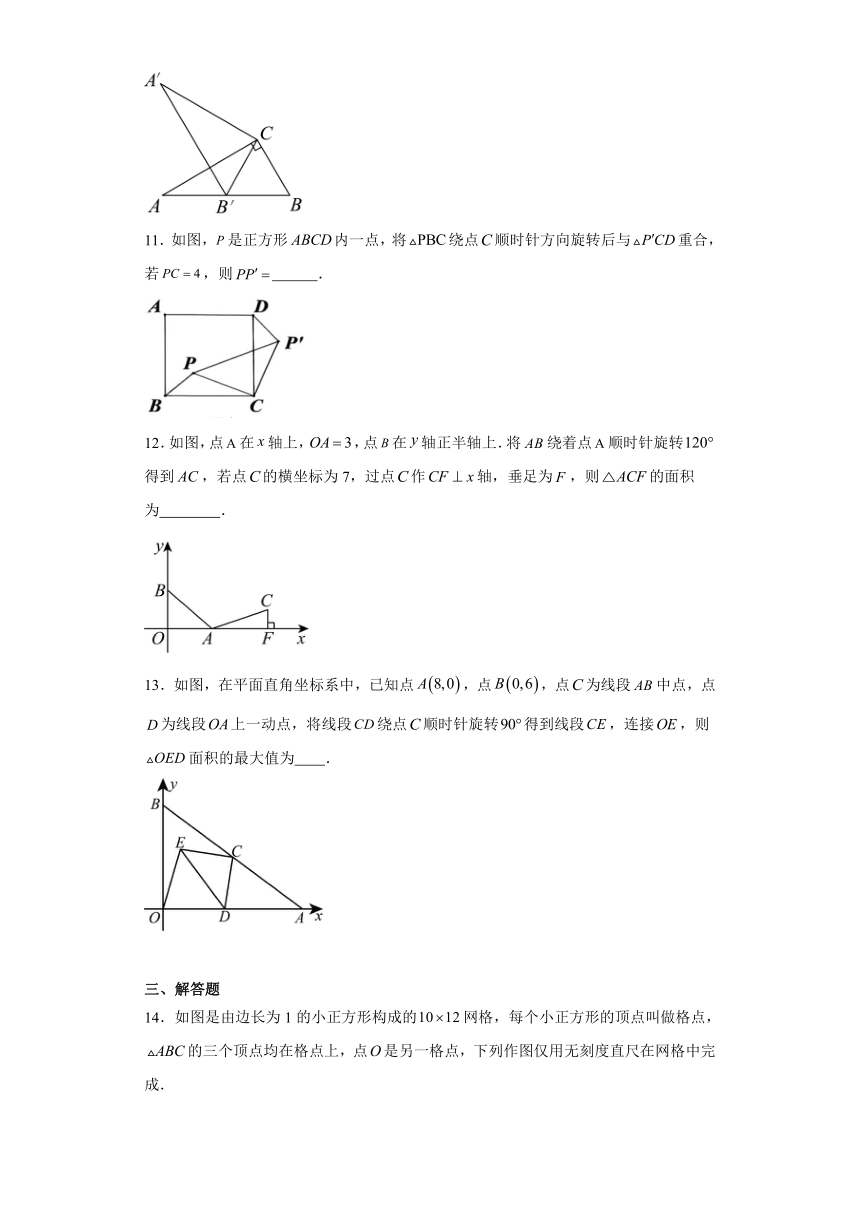
11.如图,是正方形内一点,将绕点顺时针方向旋转后与重合,若,则 .
12.如图,点在轴上,,点在轴正半轴上.将绕着点顺时针旋转得到,若点的横坐标为7,过点作轴,垂足为,则的面积为 .
13.如图,在平面直角坐标系中,已知点,点,点为线段中点,点为线段上一动点,将线段绕点顺时针旋转得到线段,连接,则面积的最大值为 .
三、解答题
14.如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点,的三个顶点均在格点上,点是另一格点,下列作图仅用无刻度直尺在网格中完成.
(1)画出关于点的中心对称图形.
(2)将绕点逆时针旋转得,画出;
(3)直接写出的形状和面积.
15.如图,为正方形内一点,连接、,将绕着点按逆时针旋转到的位置,连接,求的值.
16.如图,已知 是 绕点 顺时针方向旋转后所得的图形,点 恰好在 上,.
(1)求 的度数;
(2)求证:平分
17.在中,将绕点顺时针旋转至,将绕点逆时针旋转至,得到△,使,我们称是的“旋补三角形”,的中线叫做的“旋补中线”,点叫做“旋补中心”.
(1)当为等边三角形时,画图研究的“旋补中线”与的数量关系是_____;
(2)如图,当为任意三角形时,(1)中的结论是否成立?并给予证明;
(3)若,,求的“旋补三角形”的周长.
18.阅读与理解
图1是边长分别为m和的两个正方形纸片和叠放在一起的图形(点F,G分别在,上).
(1)操作与证明
①将图1中的正方形固定,将正方形绕点C按顺时针方向旋转,连接,,如图2所示.猜想:线段与之间的大小关系,并证明你的猜想;
②若将图1中的正方形绕点C按顺时针方向任意旋转一个角度,连接,,如图3所示.那么(1)中的结论还是否成立吗?请说明理由.
(2)操作与发现
根据上面的操作过程发现,当为________度时,线段的最大值是________;当为________度时,线段的最小值是________?
试卷第1页,共3页
参考答案:
1.A
2.C
3.A
4.D
5.D
6.C
7.C
8.C
9.
10.60
11.
12.
13.
14.(1)
(2)
(3)是等腰直角三角形,面积为5
15.
16.(1);
(2)
17.(1);
(2)结论仍然成立,
(3)的“旋补三角形”的周长.
18.(1)①,②成立
(2),;或,
答案第1页,共2页
一、单选题
1.在第四象限内有一点,且,那么点M关于原点对称的点的坐标是( )
A. B. C. D.
2.2023年10月26日,神州十七号载人飞船发射任务圆满成功.下列航天图标是中心对称图形的是( )
B.
C. D.
3.如图,把绕点顺时针旋转某个角度后得到,若,,则旋转角等于( )
A. B. C. D.
4.如图,把绕着点A顺时针方向旋转,得到,点C刚好落在边上.则( )
A. B. C. D.
5.如图,直线l是正方形的一条对称轴,l与,分别交于点M,N.,的延长线相交于点P,连接.下列三角形中,与成中心对称的是( )
A. B. C. D.
6.某个正六边形螺帽需要拧4圈才能拧紧,小梧用扳手的卡口卡住螺帽,通过转动扳手的手柄来转动螺帽(如图所示).以此方式把这个螺帽拧紧,他一共需要转动扳手的次数是( )
A.4 B.16 C.24 D.32
7.中,,将绕点O顺时针旋转,点A的对应点记为C,点B的对应点记为D,顺次连接得到四边形.所得到的四边形为( )
A.梯形 B.矩形 C.菱形 D.正方形
8.如图,在正方形中,,E为边上一点,点F在边上,且,将点E绕着点F顺时针旋转得到点G,连接,则的长的最小值为( )
A.3 B.2.5 C.4 D.
二、填空题
9.若点与点关于原点对称,则 .
10.如图,在中,,,将绕点顺时针旋转得到,其中点与点是对应点,点点是对应点,若点恰好落在边上,则旋转角的大小为 °.
11.如图,是正方形内一点,将绕点顺时针方向旋转后与重合,若,则 .
12.如图,点在轴上,,点在轴正半轴上.将绕着点顺时针旋转得到,若点的横坐标为7,过点作轴,垂足为,则的面积为 .
13.如图,在平面直角坐标系中,已知点,点,点为线段中点,点为线段上一动点,将线段绕点顺时针旋转得到线段,连接,则面积的最大值为 .
三、解答题
14.如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点,的三个顶点均在格点上,点是另一格点,下列作图仅用无刻度直尺在网格中完成.
(1)画出关于点的中心对称图形.
(2)将绕点逆时针旋转得,画出;
(3)直接写出的形状和面积.
15.如图,为正方形内一点,连接、,将绕着点按逆时针旋转到的位置,连接,求的值.
16.如图,已知 是 绕点 顺时针方向旋转后所得的图形,点 恰好在 上,.
(1)求 的度数;
(2)求证:平分
17.在中,将绕点顺时针旋转至,将绕点逆时针旋转至,得到△,使,我们称是的“旋补三角形”,的中线叫做的“旋补中线”,点叫做“旋补中心”.
(1)当为等边三角形时,画图研究的“旋补中线”与的数量关系是_____;
(2)如图,当为任意三角形时,(1)中的结论是否成立?并给予证明;
(3)若,,求的“旋补三角形”的周长.
18.阅读与理解
图1是边长分别为m和的两个正方形纸片和叠放在一起的图形(点F,G分别在,上).
(1)操作与证明
①将图1中的正方形固定,将正方形绕点C按顺时针方向旋转,连接,,如图2所示.猜想:线段与之间的大小关系,并证明你的猜想;
②若将图1中的正方形绕点C按顺时针方向任意旋转一个角度,连接,,如图3所示.那么(1)中的结论还是否成立吗?请说明理由.
(2)操作与发现
根据上面的操作过程发现,当为________度时,线段的最大值是________;当为________度时,线段的最小值是________?
试卷第1页,共3页
参考答案:
1.A
2.C
3.A
4.D
5.D
6.C
7.C
8.C
9.
10.60
11.
12.
13.
14.(1)
(2)
(3)是等腰直角三角形,面积为5
15.
16.(1);
(2)
17.(1);
(2)结论仍然成立,
(3)的“旋补三角形”的周长.
18.(1)①,②成立
(2),;或,
答案第1页,共2页
同课章节目录
