鲁教版九年级数学上册第一章反比例函数1.3反比例函数的应用学案(含答案)
文档属性
| 名称 | 鲁教版九年级数学上册第一章反比例函数1.3反比例函数的应用学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 126.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-31 09:22:58 | ||
图片预览

文档简介
鲁教版九年级数学上册第一章1.3反比例函数的应用学案
【学习目标】
1、经历分析实际问题中变量之间的关系、建立反比例函数模型,进而解决问题的过程。
2、体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力。3、运用反比例函数的图象和性质解决日常生活中的有关问题。
【学习重点】反比例函数的图象与性质的运用。
【学习难点】建立反比例函数模型,进而解决问题的过程。
学习过程
一、学习新知
某校科技小组进行野外考察,途中遇到片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利完成了任务. 如果人和木板对湿地地面的压力一定时,随着木板面积S(m2) 的变化,人和木板对地面的压强p(Pa)将如何变化
如果人和木板对湿地地面的压力合计为600 N, 那么
用含S的代数式表示p,p是S的反比例函数吗?
若是,写出解析式
当木板面积为0.2 m2时,压强是多少?
如果要求压强不超过6000 Pa,木板面积至少要多大?
在直角坐标系中,作出相应的函数图象
二、对应练习
1、(2015春 甘州区校级月考)某学校对教室采用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请你根据题中所提供的信息,解答下列问题.
(1)药物燃烧时y关于x的函数关系式为 ,药物燃烧后y与x的函数关系式为 .
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
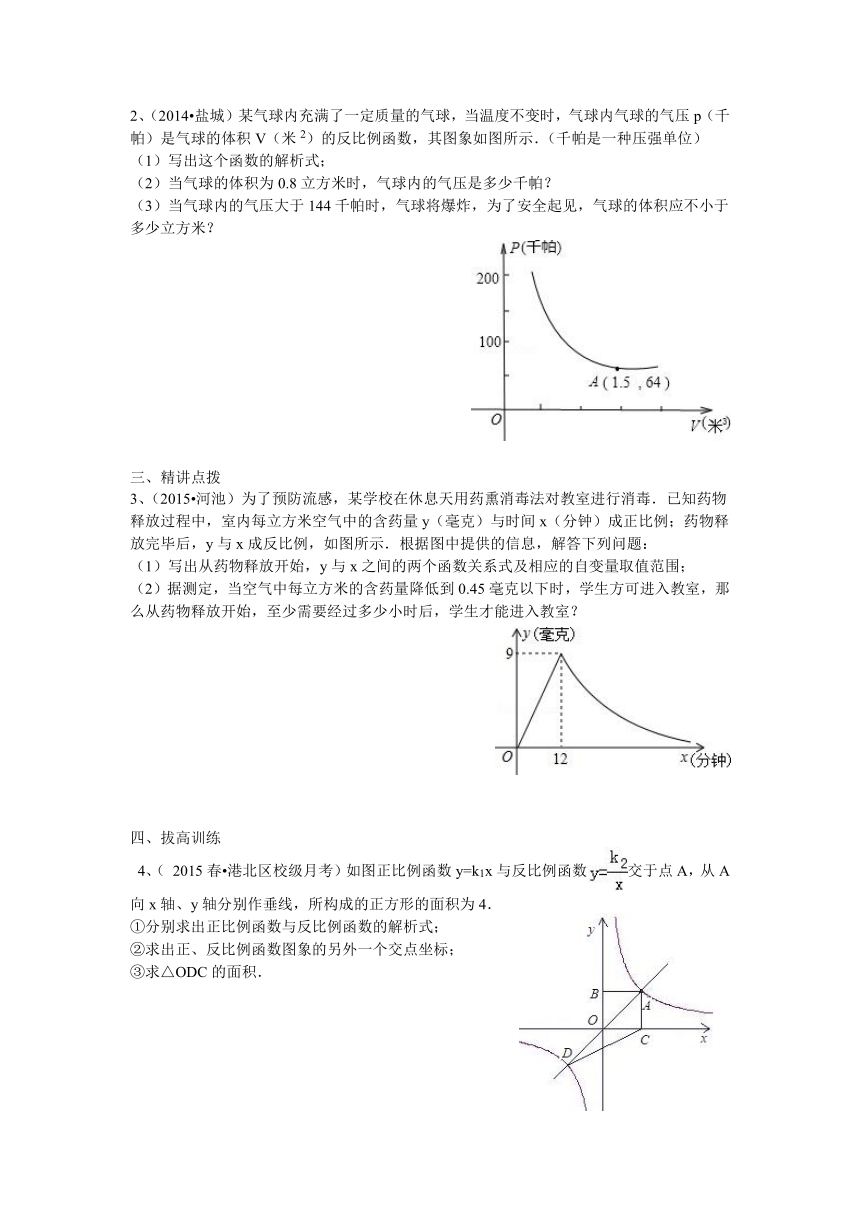
2、(2014 盐城)某气球内充满了一定质量的气球,当温度不变时,气球内气球的气压p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示.(千帕是一种压强单位)
(1)写出这个函数的解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?
三、精讲点拨
3、(2015 河池)为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
四、拔高训练
4、( 2015春 港北区校级月考)如图正比例函数y=k1x与反比例函数交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.
①分别求出正比例函数与反比例函数的解析式;
②求出正、反比例函数图象的另外一个交点坐标;
③求△ODC的面积.
五、体验中考
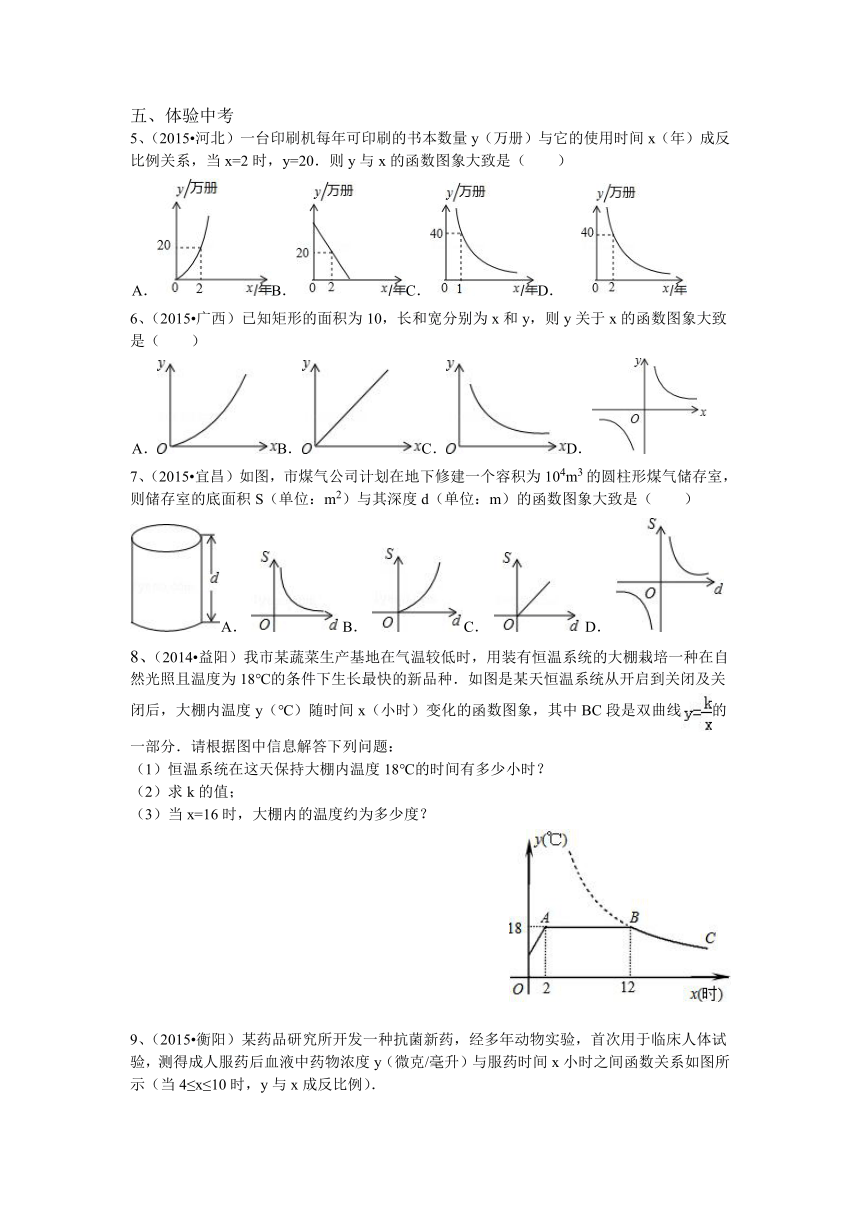
5、(2015 河北)一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A.B.C.D.
6、(2015 广西)已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是( )
A.B.C. D.
7、(2015 宜昌)如图,市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )
A. B. C. D.
8、(2014 益阳)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
9、(2015 衡阳)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
10、(2014 资阳)如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
11、(2013 昭通)如图,直线y=k1x+b(k1≠0)与双曲线y=(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(1)求直线和双曲线的解析式.
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式.
参考答案
1、 解:(1)∵药物燃烧时y与时间x成正比例,∴设 y=kx
∵(8,6)在y=kx上,8k=6,∴k=,∴y=x;
∵药物燃烧完毕后,y与x成反比例∴设y=,
∵(8,6)在 y=上,∴k=6×8=48;∴y=;故答案为:y=x,y=;
(2)3=x,x=4, 3=, x=16,16﹣4=12>10,所以此次消毒有效.
2、 解:(1)设p与V的函数的解析式为,把点A(1.5,64)代入,解得k=96.
∴这个函数的解析式为;
(2)把v=0.8代入,p=120,
当气球的体积为0.8立方米时,气球内的气压是120千帕;
(3)由p=144时,v=,∴p≤144时,v≥,
当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于立方米.
3、解:(1)药物释放过程中y与x的函数关系式为y=x(0≤x≤12)
药物释放完毕后y与x的函数关系式为y=(x≥12);
(2)=0.45,
解之得x=240(分钟)=4(小时),
答:从药物释放开始,至少需要经过4小时后,学生才能进入教室.
4、解:(1)设正比例函数y1=k1x,反比例函数y2=,
由正方形的面积可得点A的坐标(2,2),代入两函数表达式可得:k1=1,k2=4.
则正比例函数的解析式为y1=x;反比例函数的解析式为y2=.
(2)∵正、反比例函数图象的另外一个交点是D,且点D和点A关于坐标原点对称,
∵A点坐标为(2,2),∴D点坐标为(﹣2,﹣2).
即另一个交点的坐标为(﹣2,﹣2).
(3)∵△ODC是以A点横坐标的绝对值为底边,以D点纵坐标的绝对值为高,
∴S△ODC=×|xA|×|yD|=2.
C.6、C.7、A.
8、 解:(1)恒温系统在这天保持大棚温度18℃的时间为12﹣2=10小时.
(2)∵点B(12,18)在双曲线y=上,∴18=,∴解得:k=216.
(3)当x=16时,y==13.5,所以当x=16时,大棚内的温度约为13.5℃.
9、 解:(1)当0≤x≤4时,设直线解析式为:y=kx,将(4,8)代入得:8=4k,
解得:k=2,
故直线解析式为:y=2x,
当4≤x≤10时,设直反比例函数解析式为:y=,将(4,8)代入得:8=,
解得:a=32,故反比例函数解析式为:y=;
(2)当y=4,则4=2x,解得:x=2,
当y=4,则4=,解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间6小时.
10、解:(1)一次函数y=kx+b(k≠0)的图象过点P(﹣,0)和A(﹣2,1),
∴,解得,∴一次函数的解析式为y=﹣2x﹣3,
反比例函数y=(m≠0)的图象过点A(﹣2,1),∴,解得m=﹣2,
∴反比例函数的解析式为y=﹣;
(2),解得,或,∴B(,﹣4)
由图象可知,当﹣2<x<0或x>时,一次函数的函数值小于反比例函数的函数值.
11、 解:(1)∵双曲线y=经过点B(﹣2,﹣1),∴k2=2,∴双曲线的解析式为:y=,
∵点A(1,m)在双曲线y=上,∴m=2,即A(1,2),
由点A(1,2),B(﹣2,﹣1)在直线y=k1x+b上,得,
解得:,∴直线的解析式为:y=x+1;
(2)∵A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,
∴A1与A2在第三象限,A3在第一象限,即y1<0,y2<0,y3>0,
则y2<y1<y3.
【学习目标】
1、经历分析实际问题中变量之间的关系、建立反比例函数模型,进而解决问题的过程。
2、体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力。3、运用反比例函数的图象和性质解决日常生活中的有关问题。
【学习重点】反比例函数的图象与性质的运用。
【学习难点】建立反比例函数模型,进而解决问题的过程。
学习过程
一、学习新知
某校科技小组进行野外考察,途中遇到片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利完成了任务. 如果人和木板对湿地地面的压力一定时,随着木板面积S(m2) 的变化,人和木板对地面的压强p(Pa)将如何变化
如果人和木板对湿地地面的压力合计为600 N, 那么
用含S的代数式表示p,p是S的反比例函数吗?
若是,写出解析式
当木板面积为0.2 m2时,压强是多少?
如果要求压强不超过6000 Pa,木板面积至少要多大?
在直角坐标系中,作出相应的函数图象
二、对应练习
1、(2015春 甘州区校级月考)某学校对教室采用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请你根据题中所提供的信息,解答下列问题.
(1)药物燃烧时y关于x的函数关系式为 ,药物燃烧后y与x的函数关系式为 .
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
2、(2014 盐城)某气球内充满了一定质量的气球,当温度不变时,气球内气球的气压p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示.(千帕是一种压强单位)
(1)写出这个函数的解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?
三、精讲点拨
3、(2015 河池)为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
四、拔高训练
4、( 2015春 港北区校级月考)如图正比例函数y=k1x与反比例函数交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.
①分别求出正比例函数与反比例函数的解析式;
②求出正、反比例函数图象的另外一个交点坐标;
③求△ODC的面积.
五、体验中考
5、(2015 河北)一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A.B.C.D.
6、(2015 广西)已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是( )
A.B.C. D.
7、(2015 宜昌)如图,市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )
A. B. C. D.
8、(2014 益阳)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
9、(2015 衡阳)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
10、(2014 资阳)如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
11、(2013 昭通)如图,直线y=k1x+b(k1≠0)与双曲线y=(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(1)求直线和双曲线的解析式.
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式.
参考答案
1、 解:(1)∵药物燃烧时y与时间x成正比例,∴设 y=kx
∵(8,6)在y=kx上,8k=6,∴k=,∴y=x;
∵药物燃烧完毕后,y与x成反比例∴设y=,
∵(8,6)在 y=上,∴k=6×8=48;∴y=;故答案为:y=x,y=;
(2)3=x,x=4, 3=, x=16,16﹣4=12>10,所以此次消毒有效.
2、 解:(1)设p与V的函数的解析式为,把点A(1.5,64)代入,解得k=96.
∴这个函数的解析式为;
(2)把v=0.8代入,p=120,
当气球的体积为0.8立方米时,气球内的气压是120千帕;
(3)由p=144时,v=,∴p≤144时,v≥,
当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于立方米.
3、解:(1)药物释放过程中y与x的函数关系式为y=x(0≤x≤12)
药物释放完毕后y与x的函数关系式为y=(x≥12);
(2)=0.45,
解之得x=240(分钟)=4(小时),
答:从药物释放开始,至少需要经过4小时后,学生才能进入教室.
4、解:(1)设正比例函数y1=k1x,反比例函数y2=,
由正方形的面积可得点A的坐标(2,2),代入两函数表达式可得:k1=1,k2=4.
则正比例函数的解析式为y1=x;反比例函数的解析式为y2=.
(2)∵正、反比例函数图象的另外一个交点是D,且点D和点A关于坐标原点对称,
∵A点坐标为(2,2),∴D点坐标为(﹣2,﹣2).
即另一个交点的坐标为(﹣2,﹣2).
(3)∵△ODC是以A点横坐标的绝对值为底边,以D点纵坐标的绝对值为高,
∴S△ODC=×|xA|×|yD|=2.
C.6、C.7、A.
8、 解:(1)恒温系统在这天保持大棚温度18℃的时间为12﹣2=10小时.
(2)∵点B(12,18)在双曲线y=上,∴18=,∴解得:k=216.
(3)当x=16时,y==13.5,所以当x=16时,大棚内的温度约为13.5℃.
9、 解:(1)当0≤x≤4时,设直线解析式为:y=kx,将(4,8)代入得:8=4k,
解得:k=2,
故直线解析式为:y=2x,
当4≤x≤10时,设直反比例函数解析式为:y=,将(4,8)代入得:8=,
解得:a=32,故反比例函数解析式为:y=;
(2)当y=4,则4=2x,解得:x=2,
当y=4,则4=,解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间6小时.
10、解:(1)一次函数y=kx+b(k≠0)的图象过点P(﹣,0)和A(﹣2,1),
∴,解得,∴一次函数的解析式为y=﹣2x﹣3,
反比例函数y=(m≠0)的图象过点A(﹣2,1),∴,解得m=﹣2,
∴反比例函数的解析式为y=﹣;
(2),解得,或,∴B(,﹣4)
由图象可知,当﹣2<x<0或x>时,一次函数的函数值小于反比例函数的函数值.
11、 解:(1)∵双曲线y=经过点B(﹣2,﹣1),∴k2=2,∴双曲线的解析式为:y=,
∵点A(1,m)在双曲线y=上,∴m=2,即A(1,2),
由点A(1,2),B(﹣2,﹣1)在直线y=k1x+b上,得,
解得:,∴直线的解析式为:y=x+1;
(2)∵A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,
∴A1与A2在第三象限,A3在第一象限,即y1<0,y2<0,y3>0,
则y2<y1<y3.
