浙江省宁波市北仑区2023-2024学年九年级上学期期末数学试题(含答案)
文档属性
| 名称 | 浙江省宁波市北仑区2023-2024学年九年级上学期期末数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-08 18:43:20 | ||
图片预览


文档简介
二〇二三学年第一学期九年级期末测评数学卷
考生须知:
1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷.试题卷共4页,有三个大题,23个小题.满分120分,考试用时120分钟.
2.请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上.
3.答题时,把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选项位置用2B铅笔涂黑、涂满;将试题卷Ⅱ的答案用黑色字迹的钢笔或签字笔书写,答案必须按照题号顺序在答题卷Ⅱ各题目规定区域内作答,做在试题卷上或超出答题卷区域内书写的答案无效.
4.不允许使用计算器,没有近似计算要求的试题,结果都不能用近似数表示.
试题卷Ⅰ
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)
1.在平面直角坐标系中,下列二次函数的图象开口向上的是( )
A. B. C. D.
2.下列事件中是必然事件的是( )
A.从只装有3个白球的袋子中摸出一个球,是白球
B.打开电视,正在播放新闻
C.抛掷一枚硬币,落地后正面朝上
D.抛掷一个骰子,出现8点
3.若,则的值是( )
A. B. C. D.
4.已知的半径为5,若圆心到直线的距离为3,则直线与位置关系是( )
A.相切 B.相离 C.相交 D.无法确定
5.如图,在中,,,,则的值是( )
A. B. C. D.
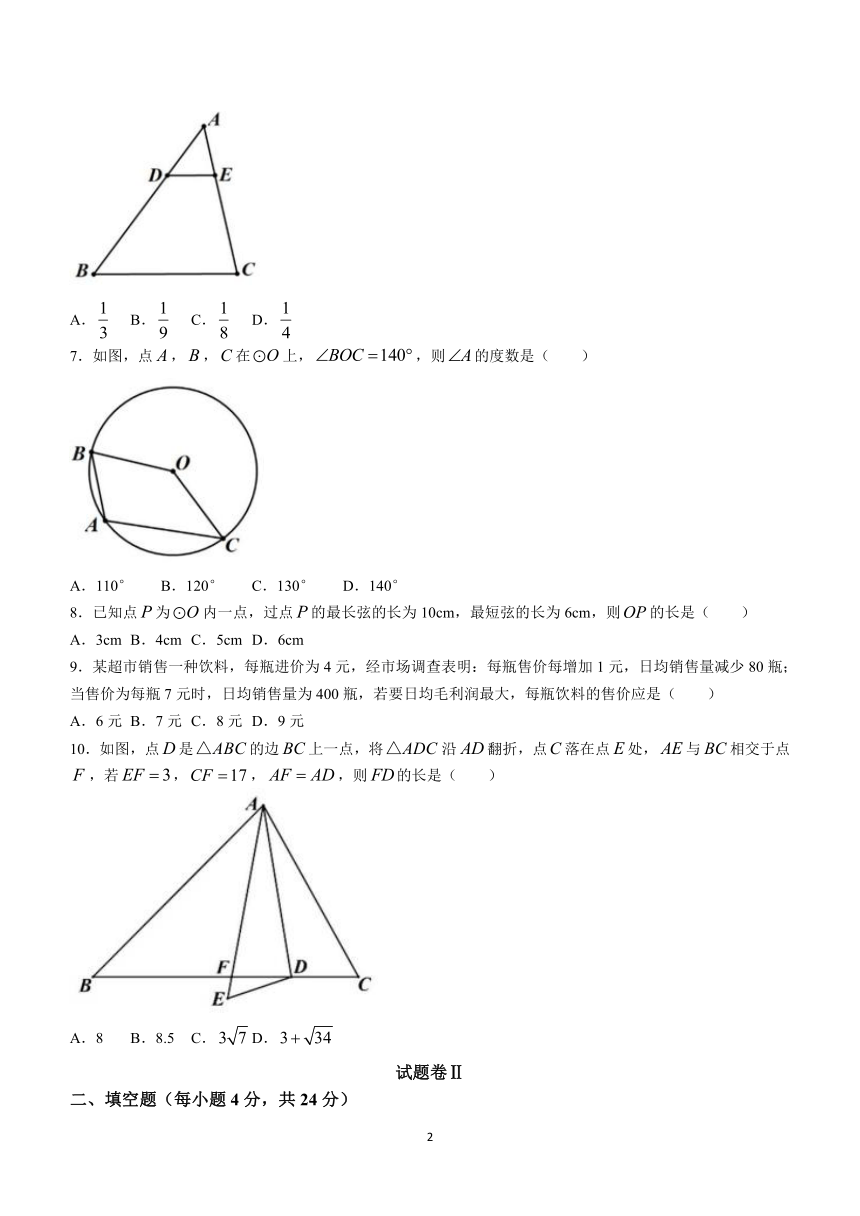
6.如图,在中,,两点分别在,边上,且,则与面积的比值是( )
A. B. C. D.
7.如图,点,,在上,,则的度数是( )
A.110° B.120° C.130° D.140°
8.已知点为内一点,过点的最长弦的长为10cm,最短弦的长为6cm,则的长是( )
A.3cm B.4cm C.5cm D.6cm
9.某超市销售一种饮料,每瓶进价为4元,经市场调查表明:每瓶售价每增加1元,日均销售量减少80瓶;当售价为每瓶7元时,日均销售量为400瓶,若要日均毛利润最大,每瓶饮料的售价应是( )
A.6元 B.7元 C.8元 D.9元
10.如图,点是的边上一点,将沿翻折,点落在点处,与相交于点,若,,,则的长是( )
A.8 B.8.5 C. D.
试题卷Ⅱ
二、填空题(每小题4分,共24分)
11.正六边形的每个内角都是______度.
12.将二次函数的图象向上平移3个单位,所得函数的表达式是______.
13.某模具厂在相同条件下抽取部分模具做尺寸检验,结果如下表所示:
抽取模具数 100 300 400 600 1000 2000 3000
合格品数 96 282 382 570 949 1900 2850
合格品频率 0.960 0.940 0.955 0.950 0.949 0.950 0.950
则该厂生产的模具是合格品的概率估计值是______.(精确到0.01)
14.如图1,宁波城区最大摩天轮“芯动北仑”已成为北仑地标性建筑.已知“芯动北仑”摩天轮半径约为26米,每个轿厢安装在摩天轮圆周30等分的分点处,如图2所示,则相邻轿厢之间的弧长为______米.(结果保留)
15.《九章算术》是我国古代数学的瑰宝,其第九卷中有著名的“勾股容圆”问题,原文为:“今有勾八步,股一十五步.问勾中容圆径几何?”意思是“今有直角三角形,较短直角边长8步,较长直角边长15步,问此直角三角形内切圆的直径是多少步?”我们用学过的知识可求该内切圆的直径是______步.
16.如图,在矩形中,点是边上一点且,延长交射线于点,连结交于点,若,则______度,______.
三、解答题(本大题有7小题,共66分)
17.(本题6分)计算:
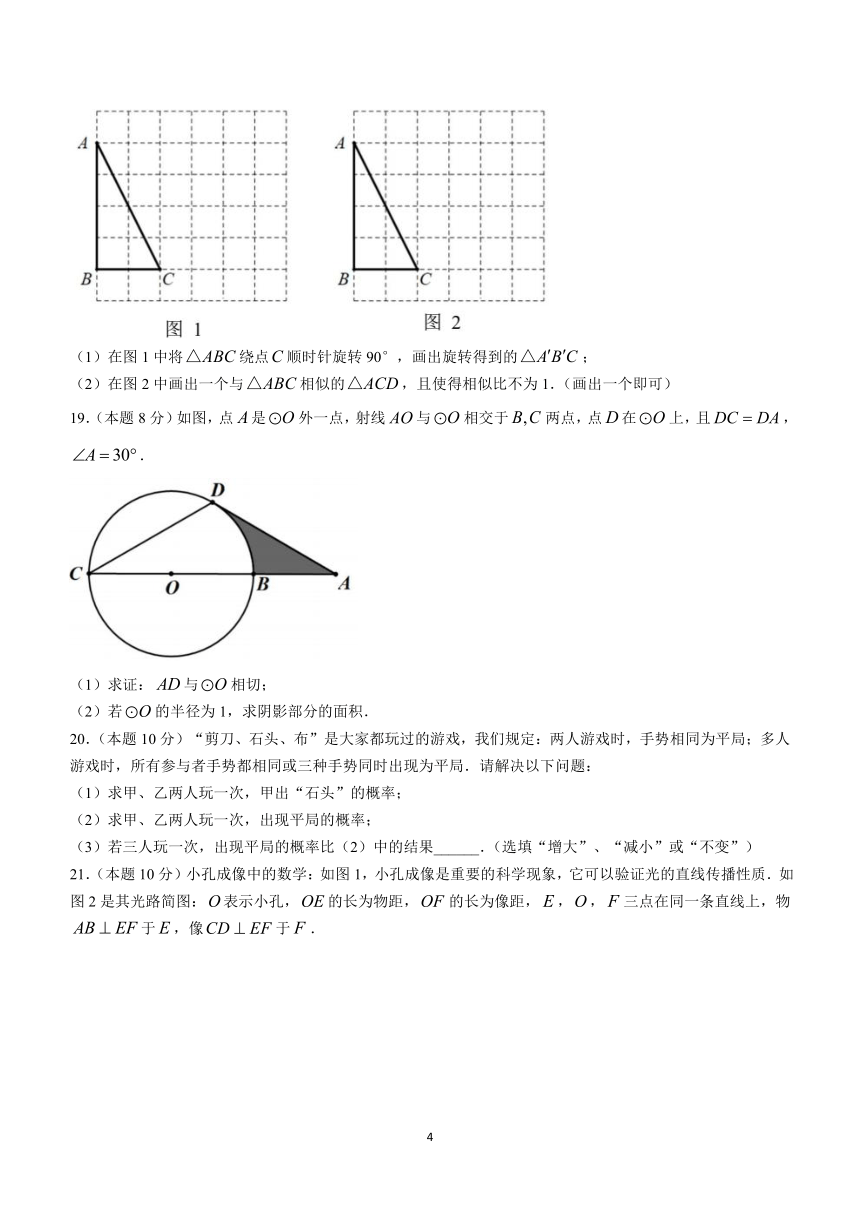
18.(本题8分)在的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图1中将绕点顺时针旋转90°,画出旋转得到的;
(2)在图2中画出一个与相似的,且使得相似比不为1.(画出一个即可)
19.(本题8分)如图,点是外一点,射线与相交于两点,点在上,且,.
(1)求证:与相切;
(2)若的半径为1,求阴影部分的面积.
20.(本题10分)“剪刀、石头、布”是大家都玩过的游戏,我们规定:两人游戏时,手势相同为平局;多人游戏时,所有参与者手势都相同或三种手势同时出现为平局.请解决以下问题:
(1)求甲、乙两人玩一次,甲出“石头”的概率;
(2)求甲、乙两人玩一次,出现平局的概率;
(3)若三人玩一次,出现平局的概率比(2)中的结果______.(选填“增大”、“减小”或“不变”)
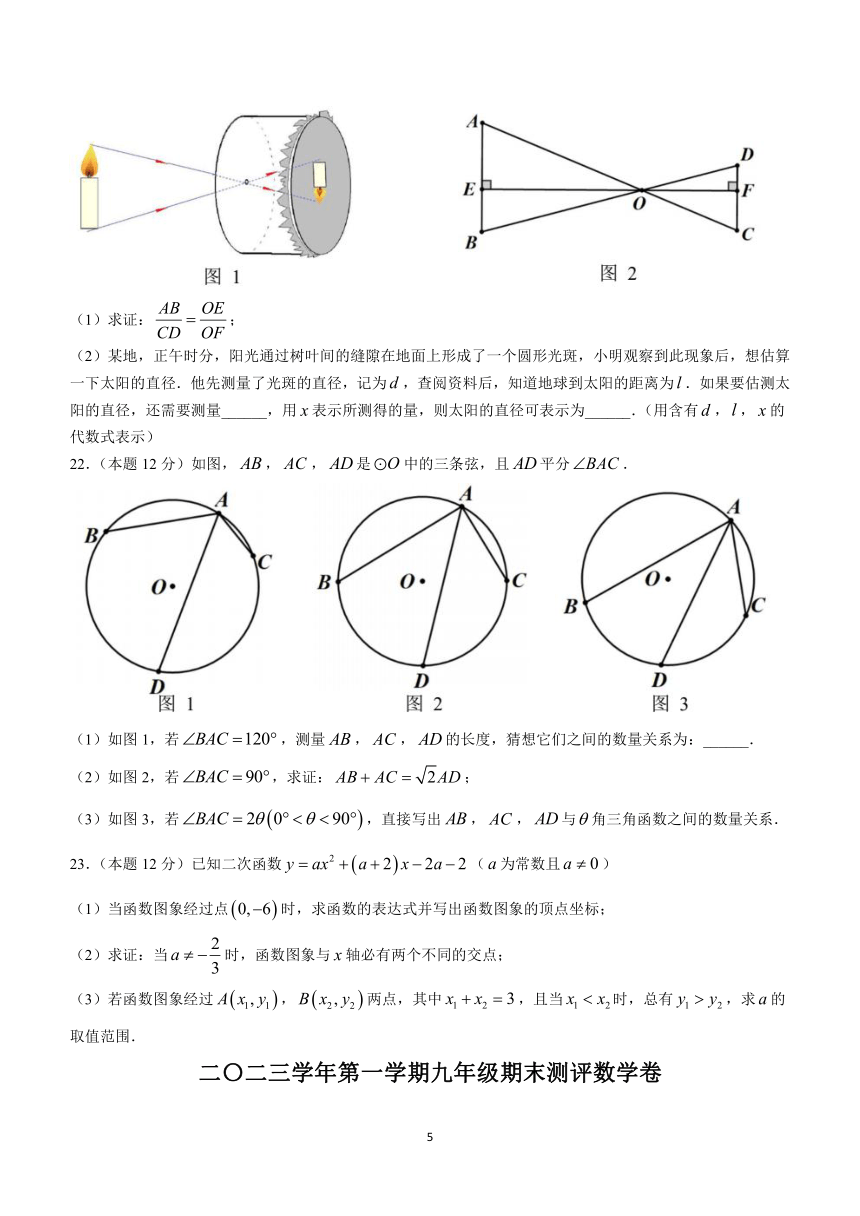
21.(本题10分)小孔成像中的数学:如图1,小孔成像是重要的科学现象,它可以验证光的直线传播性质.如图2是其光路简图:表示小孔,的长为物距,的长为像距,,,三点在同一条直线上,物于,像于.
(1)求证:;
(2)某地,正午时分,阳光通过树叶间的缝隙在地面上形成了一个圆形光斑,小明观察到此现象后,想估算一下太阳的直径.他先测量了光斑的直径,记为,查阅资料后,知道地球到太阳的距离为.如果要估测太阳的直径,还需要测量______,用表示所测得的量,则太阳的直径可表示为______.(用含有,,的代数式表示)
22.(本题12分)如图,,,是中的三条弦,且平分.
(1)如图1,若,测量,,的长度,猜想它们之间的数量关系为:______.
(2)如图2,若,求证:;
(3)如图3,若,直接写出,,与角三角函数之间的数量关系.
23.(本题12分)已知二次函数(为常数且)
(1)当函数图象经过点时,求函数的表达式并写出函数图象的顶点坐标;
(2)求证:当时,函数图象与轴必有两个不同的交点;
(3)若函数图象经过,两点,其中,且当时,总有,求的取值范围.
二〇二三学年第一学期九年级期末测评数学卷
参考答案及评分标准
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D C D B A B C A
10.分析与解答,如图
∵,∴
∵,
∴
由折叠可得:
∴,
∵,
∴,
∴
设,
∵,
∴,∴
∴
解得:,(舍)
∴,选A.
二、填空题(每小题4分,共24分)
11.120 12. 13.0.95
14. 15.6 16.
(阅卷说明:第13题写0.950不扣分;第16题每空2分;多加单位不扣分.)
三、解答题(本大题有7小题,共66分)
17.
原式
18.每小题4分.
19.(1)连结
∵,∴
∴
∴
∴,
∴与相切.
(2)∵,,,,
∴,,
∴,,
∴.
20.(1)甲可以从剪刀、石头、布中随机出一个手势
所以甲出“石头”的概率为.
(2)记剪刀、石头、布分别记作,,,
如图所示,总共9种等可能的结果,其中平局3种,所以.
(3)不变.
阅卷说明:照常理看,人数增加平局概率应当增大,但是从2人游戏到3人游戏游戏规则发生变化,从而引发这一不变的特殊情况,随着游戏人数继续增加,平局概率将自然变大,进一步可求出人平局概率为.
21.(1)∵于,于,
∴
∴,
∴,
∴.
(2)树叶缝隙到光斑中心的距离,(每空2分)
阅卷说明:第1小题得到后,直接用对应边上的高之比等于相似比得到结论不扣分;第2小题第1空只要意思表达为的长均给分,第2空由于本来就是估算,当时,中的大小相对可以忽略不计,即有,故第2空填也判定为正确.
22.(1).
(2)连结,,过点作于,于,
∵平方
∴,
又∵,
∴,
∴,
∵,
∴,
∴,
∴
∴,
∴.
∵在中,,
∴,
∴.
(3).
阅卷说明:本题第2小题证法较多,其他方法酌情给分.
23.(1)将代入函数表达式得:
解得:
∴
∴二次函数顶点坐标为.
(2)∵
当时,
∴当时,函数图象与轴必有两个不同的交点.
(3)将,两点坐标代入函数表达式得:
,,
∵,
∴,
∴,
∴,,
即:,
又∵,
∴,
∴,
解得:.
阅卷说明:本题第3小题用图象法分类讨论,酌情给分.
考生须知:
1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷.试题卷共4页,有三个大题,23个小题.满分120分,考试用时120分钟.
2.请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上.
3.答题时,把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选项位置用2B铅笔涂黑、涂满;将试题卷Ⅱ的答案用黑色字迹的钢笔或签字笔书写,答案必须按照题号顺序在答题卷Ⅱ各题目规定区域内作答,做在试题卷上或超出答题卷区域内书写的答案无效.
4.不允许使用计算器,没有近似计算要求的试题,结果都不能用近似数表示.
试题卷Ⅰ
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)
1.在平面直角坐标系中,下列二次函数的图象开口向上的是( )
A. B. C. D.
2.下列事件中是必然事件的是( )
A.从只装有3个白球的袋子中摸出一个球,是白球
B.打开电视,正在播放新闻
C.抛掷一枚硬币,落地后正面朝上
D.抛掷一个骰子,出现8点
3.若,则的值是( )
A. B. C. D.
4.已知的半径为5,若圆心到直线的距离为3,则直线与位置关系是( )
A.相切 B.相离 C.相交 D.无法确定
5.如图,在中,,,,则的值是( )
A. B. C. D.
6.如图,在中,,两点分别在,边上,且,则与面积的比值是( )
A. B. C. D.
7.如图,点,,在上,,则的度数是( )
A.110° B.120° C.130° D.140°
8.已知点为内一点,过点的最长弦的长为10cm,最短弦的长为6cm,则的长是( )
A.3cm B.4cm C.5cm D.6cm
9.某超市销售一种饮料,每瓶进价为4元,经市场调查表明:每瓶售价每增加1元,日均销售量减少80瓶;当售价为每瓶7元时,日均销售量为400瓶,若要日均毛利润最大,每瓶饮料的售价应是( )
A.6元 B.7元 C.8元 D.9元
10.如图,点是的边上一点,将沿翻折,点落在点处,与相交于点,若,,,则的长是( )
A.8 B.8.5 C. D.
试题卷Ⅱ
二、填空题(每小题4分,共24分)
11.正六边形的每个内角都是______度.
12.将二次函数的图象向上平移3个单位,所得函数的表达式是______.
13.某模具厂在相同条件下抽取部分模具做尺寸检验,结果如下表所示:
抽取模具数 100 300 400 600 1000 2000 3000
合格品数 96 282 382 570 949 1900 2850
合格品频率 0.960 0.940 0.955 0.950 0.949 0.950 0.950
则该厂生产的模具是合格品的概率估计值是______.(精确到0.01)
14.如图1,宁波城区最大摩天轮“芯动北仑”已成为北仑地标性建筑.已知“芯动北仑”摩天轮半径约为26米,每个轿厢安装在摩天轮圆周30等分的分点处,如图2所示,则相邻轿厢之间的弧长为______米.(结果保留)
15.《九章算术》是我国古代数学的瑰宝,其第九卷中有著名的“勾股容圆”问题,原文为:“今有勾八步,股一十五步.问勾中容圆径几何?”意思是“今有直角三角形,较短直角边长8步,较长直角边长15步,问此直角三角形内切圆的直径是多少步?”我们用学过的知识可求该内切圆的直径是______步.
16.如图,在矩形中,点是边上一点且,延长交射线于点,连结交于点,若,则______度,______.
三、解答题(本大题有7小题,共66分)
17.(本题6分)计算:
18.(本题8分)在的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图1中将绕点顺时针旋转90°,画出旋转得到的;
(2)在图2中画出一个与相似的,且使得相似比不为1.(画出一个即可)
19.(本题8分)如图,点是外一点,射线与相交于两点,点在上,且,.
(1)求证:与相切;
(2)若的半径为1,求阴影部分的面积.
20.(本题10分)“剪刀、石头、布”是大家都玩过的游戏,我们规定:两人游戏时,手势相同为平局;多人游戏时,所有参与者手势都相同或三种手势同时出现为平局.请解决以下问题:
(1)求甲、乙两人玩一次,甲出“石头”的概率;
(2)求甲、乙两人玩一次,出现平局的概率;
(3)若三人玩一次,出现平局的概率比(2)中的结果______.(选填“增大”、“减小”或“不变”)
21.(本题10分)小孔成像中的数学:如图1,小孔成像是重要的科学现象,它可以验证光的直线传播性质.如图2是其光路简图:表示小孔,的长为物距,的长为像距,,,三点在同一条直线上,物于,像于.
(1)求证:;
(2)某地,正午时分,阳光通过树叶间的缝隙在地面上形成了一个圆形光斑,小明观察到此现象后,想估算一下太阳的直径.他先测量了光斑的直径,记为,查阅资料后,知道地球到太阳的距离为.如果要估测太阳的直径,还需要测量______,用表示所测得的量,则太阳的直径可表示为______.(用含有,,的代数式表示)
22.(本题12分)如图,,,是中的三条弦,且平分.
(1)如图1,若,测量,,的长度,猜想它们之间的数量关系为:______.
(2)如图2,若,求证:;
(3)如图3,若,直接写出,,与角三角函数之间的数量关系.
23.(本题12分)已知二次函数(为常数且)
(1)当函数图象经过点时,求函数的表达式并写出函数图象的顶点坐标;
(2)求证:当时,函数图象与轴必有两个不同的交点;
(3)若函数图象经过,两点,其中,且当时,总有,求的取值范围.
二〇二三学年第一学期九年级期末测评数学卷
参考答案及评分标准
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D C D B A B C A
10.分析与解答,如图
∵,∴
∵,
∴
由折叠可得:
∴,
∵,
∴,
∴
设,
∵,
∴,∴
∴
解得:,(舍)
∴,选A.
二、填空题(每小题4分,共24分)
11.120 12. 13.0.95
14. 15.6 16.
(阅卷说明:第13题写0.950不扣分;第16题每空2分;多加单位不扣分.)
三、解答题(本大题有7小题,共66分)
17.
原式
18.每小题4分.
19.(1)连结
∵,∴
∴
∴
∴,
∴与相切.
(2)∵,,,,
∴,,
∴,,
∴.
20.(1)甲可以从剪刀、石头、布中随机出一个手势
所以甲出“石头”的概率为.
(2)记剪刀、石头、布分别记作,,,
如图所示,总共9种等可能的结果,其中平局3种,所以.
(3)不变.
阅卷说明:照常理看,人数增加平局概率应当增大,但是从2人游戏到3人游戏游戏规则发生变化,从而引发这一不变的特殊情况,随着游戏人数继续增加,平局概率将自然变大,进一步可求出人平局概率为.
21.(1)∵于,于,
∴
∴,
∴,
∴.
(2)树叶缝隙到光斑中心的距离,(每空2分)
阅卷说明:第1小题得到后,直接用对应边上的高之比等于相似比得到结论不扣分;第2小题第1空只要意思表达为的长均给分,第2空由于本来就是估算,当时,中的大小相对可以忽略不计,即有,故第2空填也判定为正确.
22.(1).
(2)连结,,过点作于,于,
∵平方
∴,
又∵,
∴,
∴,
∵,
∴,
∴,
∴
∴,
∴.
∵在中,,
∴,
∴.
(3).
阅卷说明:本题第2小题证法较多,其他方法酌情给分.
23.(1)将代入函数表达式得:
解得:
∴
∴二次函数顶点坐标为.
(2)∵
当时,
∴当时,函数图象与轴必有两个不同的交点.
(3)将,两点坐标代入函数表达式得:
,,
∵,
∴,
∴,
∴,,
即:,
又∵,
∴,
∴,
解得:.
阅卷说明:本题第3小题用图象法分类讨论,酌情给分.
同课章节目录
