7.3图形的平移 讲义 2023-2024学年苏科版数学七年级下册
文档属性
| 名称 | 7.3图形的平移 讲义 2023-2024学年苏科版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-09 00:00:00 | ||
图片预览



文档简介
7.3图形的平移
教学目的: 了解图形的平移变换,知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质,能用平移变换有关知识说明一些简单问题及进行图形设计.
教学重难点: 1、图形的平移 2、利用平移的性质求解 3、利用平移解决实际问题
知识梳理
【知识点一】平行的概念 1. 定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移. 特别说明: (1)图形的平移的两要素:平移的方向与平移的距离. (2)图形的平移不改变图形的形状与大小,只改变图形的位置. 2. 性质: 图形的平移实质上是将图形上所有点沿同一方向移动相同的距离,平移不改变线段、角的大小,具体来说: (1)平移后,对应线段平行且相等; (2)平移后,对应角相等; (3)平移后,对应点所连线段平行且相等; (4)平移后,新图形与原图形是一对全等图形. 3. 作图: 平移作图的步骤: (1)定:根据题目要求,确定平移的方向和距离; (2)找:找出确定图形形状的关键点; (3)移:按平移的方向和距离确定各关键点平移后的对应点; (4)连:按原图顺序依次连接各对应点. 确定一个图形平移后的位置需要三个条件:①图形原位置;②平移的方向;③平移的距离.
典型例题
【例1】下面的四个图形中,能够通过基本图形平移得到的图形有( ) A.1个 B.2个 C.3个 D.4个 【例2】下列命题正确的是( ) (1)两条直线被第三条直线所截,同位角相等; (2)在同一平面内,过一点有且只有一条直线与已知直线垂直; (3)平移前后连接各组对应点的线段平行且相等; (4)从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离; (5)在同一平面内,三条直线的交点个数有三种情况. A.0个 B.1个 C.2个 D.3个 【例3】如图,从A到B有①②③三条路可以走,每条路长分别为l,m,n,则l,m,n的大小关系是( ) A. B. C. D. 【例4】如图,是由边长为1个单位长度的小正方形组成的网格,ABC的顶点都在格点上,将ABC向右平移1个单位长度,再向上平移3个单位长度,得到DEF,其中点A、B、C的对应点分别为点 D、E、F. (1)在图中画出平移后的△DEF. (2)过点A画BC的垂线AH,垂足为点H (3)在整个平移过程中,线段AC扫过的面积为 .
举一反三
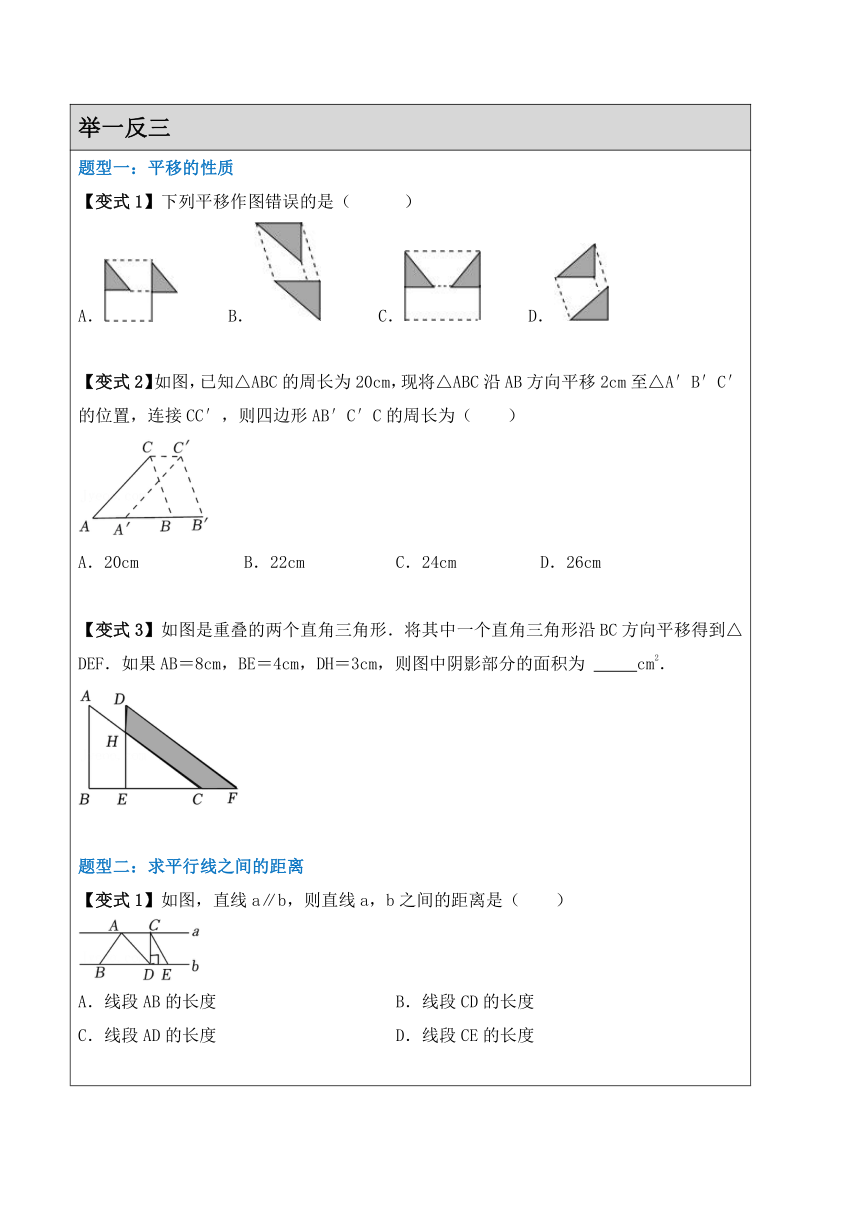
题型一:平移的性质 【变式1】下列平移作图错误的是( ) A. B. C. D. 【变式2】如图,已知△ABC的周长为20cm,现将△ABC沿AB方向平移2cm至△A′B′C′的位置,连接CC′,则四边形AB′C′C的周长为( ) A.20cm B.22cm C.24cm D.26cm 【变式3】如图是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分的面积为 cm2. 题型二:求平行线之间的距离 【变式1】如图,直线a∥b,则直线a,b之间的距离是( ) A.线段AB的长度 B.线段CD的长度 C.线段AD的长度 D.线段CE的长度 【变式2】如图,直线l1∥l2,其中P在l1上,A、B、C、D在l2上,且PB⊥l2,则l1与l2间的距离是( ) A.线段 PA 的长度 B.线段 PB 的长度 C.线段 PC 的长度 D.线段 PD 的长度 【变式3】 在同一平面内,设a、b、c是三条互相平行的直线,已知a与b间的距离为5cm,b与c间的距离为2cm,则a与c间的距离为( )cm. A.3 B.7 C.3或7 D.2或3 题型三:平移在实际生活中的应用 【变式1】在以下现象中,属于平移的是 ①在荡秋千的小朋友; ②水平传送带上的物体 ③宇宙中行星的运动 ④打气筒打气时,活塞的运动. A.①② B.③④ C.②③ D.②④ 【变式2】如图,长为50m,宽为30m的长方形地块上,有纵横交错的几条小路,宽均为1m,其它部分均种植草坪,则种植草坪的面积为( ) A.1344m2 B.1421m2 C.1431m2 D.1341m2 【变式3】如图,在一块长为a米,宽为b米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1米就是它的右边线,求: (1)用含a,b的式子表示绿地面积; (2)当米,米时,绿地面积是多少平方米? 题型四:平移性质的综合运用 【变式1】如图,将直角沿边的方向平移到的位置,连接,若,,则的长为( ) A.4 B.6 C.8 D.12 【变式2】如图,将沿方向平移得到△,若的周长为,则四边形的周长为 . 【变式3】如图,已知三角形,是的平分线,平移三角形,使点移动到点,点的对应点是,点的对应点是. (1)在图中画出平移后的三角形; (2)画出点到线段的垂线段; (3)若,与相交于点,则___________°,______°.
小试牛刀
一、选择题(共5题) 1.2022年02月04日至02月20日,第24届冬季奥林匹克运动会在我国北京和张家口举行,该次盛会的吉祥物“冰墩墩”以熊猫为原型进行创意设计,如图所示是“冰墩墩”的图案.A,B,C,D中哪一个图案可以通过平移图1得到( ) A.B. C. D. 2.如图,将△ABC沿BC方向平移1cm得到对应的△A′B′C′.若B′C=2cm,则BC′的长是( ) A.2cm B.3cm C.4cm D.5cm 3.下列说法正确的是( ) A.同旁内角互补 B.平移不改变直线的方向 C.过一点有且只有一条直线与已知直线垂直 D.从直线外一点到这条直线的垂线段,叫做点到直线的距离 4.如图,长方形ABCD的长AB为8,宽AD为6,将这个长方形向上平移3个单位,再向左平移2个单位,得到长方形EFGH,则阴影部分的面积为( ) A.30 B.32 C.36 D.40 5.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动( ) A.8格 B.9格 C.11格 D.12格 二、填空题(共5题) 6.如果将一个四边形向上平移得到四边形,点是点的对应点,则线段___________cm 7.如图,△ABC沿BC所在直线向右平移得到△DEF,若EC=2,BF=8,则BE=___. 8.在一块长,宽的草坪上修筑宽的小路(如图),则种草地面的面积是_____. 9.如图,在三角形中,.把三角形沿方向平移,得到三角形,连接,则四边形的周长为 . 10.边长为2的等边与等边互相重合,将沿直线向左平移个单位长度,将向右也平移个单位长度,如图,当、是线段的三等分点时,的值为 . 三、解答题(共5题) 11.如图,经过平移,的顶点A移到了点D. (1)指出平移的方向和平移的距离; (2)画出平移后的三角形. 12.如图,在每个小正方形边长为1的方格纸中,点A、B、A1都在方格纸的格点上. (1)平移线段AB,使点A与点A1重合,点B与点B1重合,画出线段A1B1; (2)连接AA1、BB1,AA1与BB1的关系是 ; (3)四边形ABB1A1的面积是 . 13.某公园准备修建一块长方形草坪,长为25米,宽为20米.并在草坪上修建如图所示的十字路,已知十字路宽米,回答下列问题: (1)修建的十字路面积是多少平方米? (2)如果十字路宽3米,那么草坪(阴影部分)的面积是多少? 14.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C. (1)若∠1=60°,求∠2的度数; (2)若AC=5,AB=12,BC=13,求直线a与b的距离. 15.如图 (1)动手操作如图1,在的网格中,将线段向右平移,得到线段,连接,. ①线段平移的距离是 ; ②四边形的面积 ; (2)如图2,在的网格中,将折线向右平移3个单位长度,得到折线. ①画出平移后的折线; ②连接,,多边形的面积 ; (3)拓展延伸如图3,在一块长为米,宽为米的长方形草坪上,修建一条宽为米的小路(小路宽度处处相同),直接写出剩下的草坪面积 .
教学目的: 了解图形的平移变换,知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质,能用平移变换有关知识说明一些简单问题及进行图形设计.
教学重难点: 1、图形的平移 2、利用平移的性质求解 3、利用平移解决实际问题
知识梳理
【知识点一】平行的概念 1. 定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移. 特别说明: (1)图形的平移的两要素:平移的方向与平移的距离. (2)图形的平移不改变图形的形状与大小,只改变图形的位置. 2. 性质: 图形的平移实质上是将图形上所有点沿同一方向移动相同的距离,平移不改变线段、角的大小,具体来说: (1)平移后,对应线段平行且相等; (2)平移后,对应角相等; (3)平移后,对应点所连线段平行且相等; (4)平移后,新图形与原图形是一对全等图形. 3. 作图: 平移作图的步骤: (1)定:根据题目要求,确定平移的方向和距离; (2)找:找出确定图形形状的关键点; (3)移:按平移的方向和距离确定各关键点平移后的对应点; (4)连:按原图顺序依次连接各对应点. 确定一个图形平移后的位置需要三个条件:①图形原位置;②平移的方向;③平移的距离.
典型例题
【例1】下面的四个图形中,能够通过基本图形平移得到的图形有( ) A.1个 B.2个 C.3个 D.4个 【例2】下列命题正确的是( ) (1)两条直线被第三条直线所截,同位角相等; (2)在同一平面内,过一点有且只有一条直线与已知直线垂直; (3)平移前后连接各组对应点的线段平行且相等; (4)从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离; (5)在同一平面内,三条直线的交点个数有三种情况. A.0个 B.1个 C.2个 D.3个 【例3】如图,从A到B有①②③三条路可以走,每条路长分别为l,m,n,则l,m,n的大小关系是( ) A. B. C. D. 【例4】如图,是由边长为1个单位长度的小正方形组成的网格,ABC的顶点都在格点上,将ABC向右平移1个单位长度,再向上平移3个单位长度,得到DEF,其中点A、B、C的对应点分别为点 D、E、F. (1)在图中画出平移后的△DEF. (2)过点A画BC的垂线AH,垂足为点H (3)在整个平移过程中,线段AC扫过的面积为 .
举一反三
题型一:平移的性质 【变式1】下列平移作图错误的是( ) A. B. C. D. 【变式2】如图,已知△ABC的周长为20cm,现将△ABC沿AB方向平移2cm至△A′B′C′的位置,连接CC′,则四边形AB′C′C的周长为( ) A.20cm B.22cm C.24cm D.26cm 【变式3】如图是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分的面积为 cm2. 题型二:求平行线之间的距离 【变式1】如图,直线a∥b,则直线a,b之间的距离是( ) A.线段AB的长度 B.线段CD的长度 C.线段AD的长度 D.线段CE的长度 【变式2】如图,直线l1∥l2,其中P在l1上,A、B、C、D在l2上,且PB⊥l2,则l1与l2间的距离是( ) A.线段 PA 的长度 B.线段 PB 的长度 C.线段 PC 的长度 D.线段 PD 的长度 【变式3】 在同一平面内,设a、b、c是三条互相平行的直线,已知a与b间的距离为5cm,b与c间的距离为2cm,则a与c间的距离为( )cm. A.3 B.7 C.3或7 D.2或3 题型三:平移在实际生活中的应用 【变式1】在以下现象中,属于平移的是 ①在荡秋千的小朋友; ②水平传送带上的物体 ③宇宙中行星的运动 ④打气筒打气时,活塞的运动. A.①② B.③④ C.②③ D.②④ 【变式2】如图,长为50m,宽为30m的长方形地块上,有纵横交错的几条小路,宽均为1m,其它部分均种植草坪,则种植草坪的面积为( ) A.1344m2 B.1421m2 C.1431m2 D.1341m2 【变式3】如图,在一块长为a米,宽为b米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1米就是它的右边线,求: (1)用含a,b的式子表示绿地面积; (2)当米,米时,绿地面积是多少平方米? 题型四:平移性质的综合运用 【变式1】如图,将直角沿边的方向平移到的位置,连接,若,,则的长为( ) A.4 B.6 C.8 D.12 【变式2】如图,将沿方向平移得到△,若的周长为,则四边形的周长为 . 【变式3】如图,已知三角形,是的平分线,平移三角形,使点移动到点,点的对应点是,点的对应点是. (1)在图中画出平移后的三角形; (2)画出点到线段的垂线段; (3)若,与相交于点,则___________°,______°.
小试牛刀
一、选择题(共5题) 1.2022年02月04日至02月20日,第24届冬季奥林匹克运动会在我国北京和张家口举行,该次盛会的吉祥物“冰墩墩”以熊猫为原型进行创意设计,如图所示是“冰墩墩”的图案.A,B,C,D中哪一个图案可以通过平移图1得到( ) A.B. C. D. 2.如图,将△ABC沿BC方向平移1cm得到对应的△A′B′C′.若B′C=2cm,则BC′的长是( ) A.2cm B.3cm C.4cm D.5cm 3.下列说法正确的是( ) A.同旁内角互补 B.平移不改变直线的方向 C.过一点有且只有一条直线与已知直线垂直 D.从直线外一点到这条直线的垂线段,叫做点到直线的距离 4.如图,长方形ABCD的长AB为8,宽AD为6,将这个长方形向上平移3个单位,再向左平移2个单位,得到长方形EFGH,则阴影部分的面积为( ) A.30 B.32 C.36 D.40 5.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动( ) A.8格 B.9格 C.11格 D.12格 二、填空题(共5题) 6.如果将一个四边形向上平移得到四边形,点是点的对应点,则线段___________cm 7.如图,△ABC沿BC所在直线向右平移得到△DEF,若EC=2,BF=8,则BE=___. 8.在一块长,宽的草坪上修筑宽的小路(如图),则种草地面的面积是_____. 9.如图,在三角形中,.把三角形沿方向平移,得到三角形,连接,则四边形的周长为 . 10.边长为2的等边与等边互相重合,将沿直线向左平移个单位长度,将向右也平移个单位长度,如图,当、是线段的三等分点时,的值为 . 三、解答题(共5题) 11.如图,经过平移,的顶点A移到了点D. (1)指出平移的方向和平移的距离; (2)画出平移后的三角形. 12.如图,在每个小正方形边长为1的方格纸中,点A、B、A1都在方格纸的格点上. (1)平移线段AB,使点A与点A1重合,点B与点B1重合,画出线段A1B1; (2)连接AA1、BB1,AA1与BB1的关系是 ; (3)四边形ABB1A1的面积是 . 13.某公园准备修建一块长方形草坪,长为25米,宽为20米.并在草坪上修建如图所示的十字路,已知十字路宽米,回答下列问题: (1)修建的十字路面积是多少平方米? (2)如果十字路宽3米,那么草坪(阴影部分)的面积是多少? 14.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C. (1)若∠1=60°,求∠2的度数; (2)若AC=5,AB=12,BC=13,求直线a与b的距离. 15.如图 (1)动手操作如图1,在的网格中,将线段向右平移,得到线段,连接,. ①线段平移的距离是 ; ②四边形的面积 ; (2)如图2,在的网格中,将折线向右平移3个单位长度,得到折线. ①画出平移后的折线; ②连接,,多边形的面积 ; (3)拓展延伸如图3,在一块长为米,宽为米的长方形草坪上,修建一条宽为米的小路(小路宽度处处相同),直接写出剩下的草坪面积 .
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
