第三单元第一课时 圆柱(同步练习) 六年级下册数学人教版(无答案)
文档属性
| 名称 | 第三单元第一课时 圆柱(同步练习) 六年级下册数学人教版(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-11 09:01:21 | ||
图片预览


文档简介
六年级下册人教版数学第三单元第一课时 圆柱
第1课时 圆柱的认识(1)
1. 填空。
(1)圆柱是由( )个面围成的。 圆柱的上、下两个面叫做( )。 圆柱周围的面(上、下底面除外)叫做( )。 圆柱的两个底面之间的距离叫做( ),圆柱有( )条高。
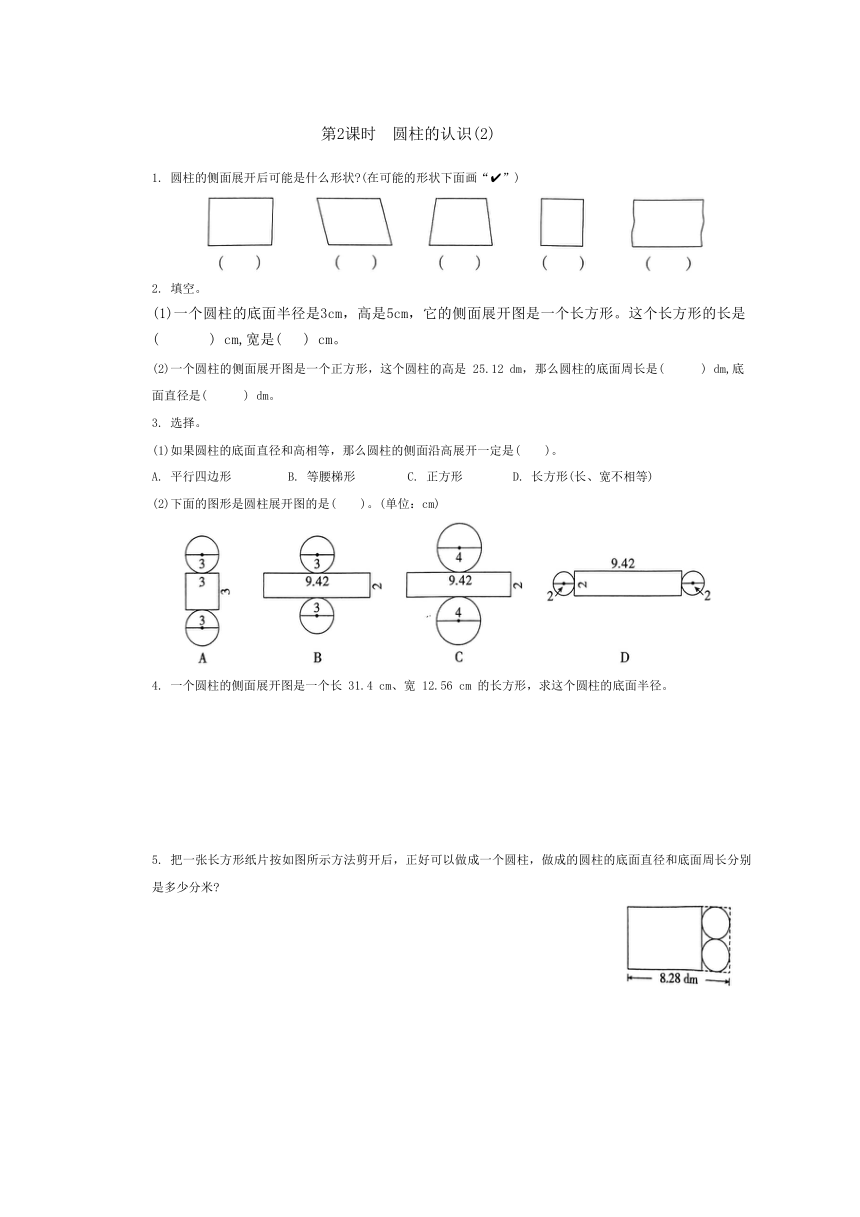
(2)下面的图形是圆柱的在括号里画“ ”,不是圆柱的画“×”。
2. 下面各图中h 表示的是圆柱的高吗 是的在括号里画“ ”,不是的画“×”。
3. 转动长方形ABCD,生成下面的两个圆柱。
(1)圆柱甲是以长方形的( )边所在的直线为轴旋转而成的,底面半径是( ),高是( )。
(2)圆柱乙是以长方形的( )边所在的直线为轴旋转而成的,底面半径是( ),高是( ) 。
4. 一个底面周长是9.42 cm、高是6 cm的圆柱,沿底面直径垂直把它切割成完全相同的两部分后,切割面的面积一共是多少平方厘米
第2课时 圆柱的认识(2)
1. 圆柱的侧面展开后可能是什么形状 (在可能的形状下面画“ ”)
2. 填空。
(1)一个圆柱的底面半径是3cm,高是5cm,它的侧面展开图是一个长方形。这个长方形的长是( ) cm,宽是( ) cm。
(2)一个圆柱的侧面展开图是一个正方形,这个圆柱的高是 25.12 dm,那么圆柱的底面周长是( ) dm,底面直径是( ) dm。
3. 选择。
(1)如果圆柱的底面直径和高相等,那么圆柱的侧面沿高展开一定是( )。
A. 平行四边形 B. 等腰梯形 C. 正方形 D. 长方形(长、宽不相等)
(2)下面的图形是圆柱展开图的是( )。(单位:cm)
4. 一个圆柱的侧面展开图是一个长 31.4 cm、宽 12.56 cm 的长方形,求这个圆柱的底面半径。
5. 把一张长方形纸片按如图所示方法剪开后,正好可以做成一个圆柱,做成的圆柱的底面直径和底面周长分别是多少分米
第3课时 圆柱的表面积(1)
1. 填空。
(1)一个圆柱的侧面积是 9.42 cm ,底面积是 3.14 cm ,它的表面积是( )cm 。
(2)一个圆柱的侧面展开图是一个长 5.2 cm、宽 4 cm 的长方形,这个圆柱的侧面积是( )cm 。
2. 选择。
(1)做一个无盖的圆柱形水桶,求至少需要多少铁皮,就是求圆柱的( )。
A. 底面积 B. 侧面积 C. 表面积 D. 侧面积+一个底面积
(2)一个圆柱的侧面积是 25.12 dm ,底面周长是 3.14 dm,它的高是( )。
A. 2 dm B. 4 dm C. 8 dm D. 16 dm
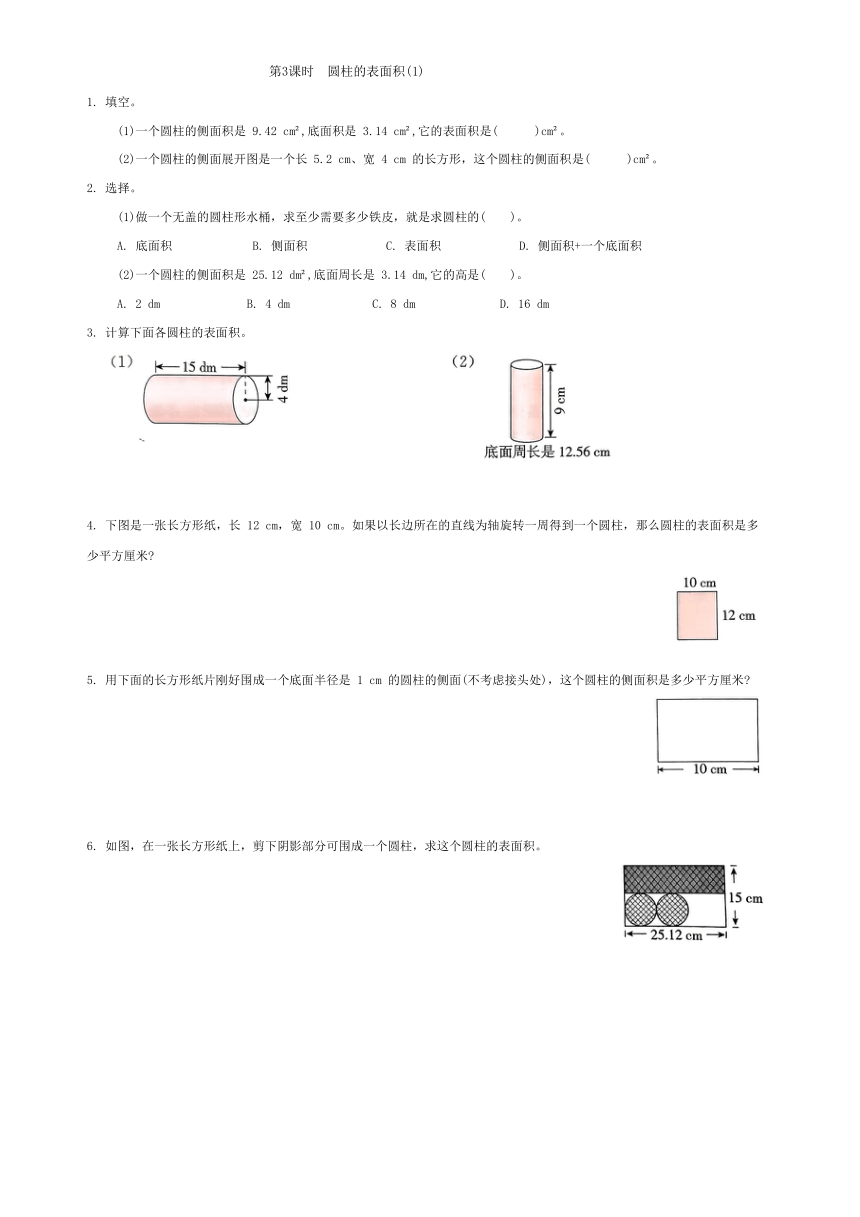
3. 计算下面各圆柱的表面积。
4. 下图是一张长方形纸,长 12 cm,宽 10 cm。如果以长边所在的直线为轴旋转一周得到一个圆柱,那么圆柱的表面积是多少平方厘米
5. 用下面的长方形纸片刚好围成一个底面半径是 1 cm 的圆柱的侧面(不考虑接头处),这个圆柱的侧面积是多少平方厘米
6. 如图,在一张长方形纸上,剪下阴影部分可围成一个圆柱,求这个圆柱的表面积。
第4课时 圆柱的表面积(2)
1. 填空。
(1)做一个圆柱形封闭式铁皮油桶,高 18 dm,底面直径是高的 / ,至少需要( )dm 铁皮。(得数保留整数)
(1)用铁皮制作 5 节通风管,每节长1m,底面半径是 10 cm,至少需要( )m 的铁皮。
A. 0.628 B. 3.14 C. 6.28 D. 31.4
(2)一个圆柱的侧面展开图是一个正方形。这个圆柱底面直径与高的比是( )。
A. 1 : π B. 1 ∶ 2π C. 1∶4π D. 2: π
3. 祈年殿是北京天坛公园的主要建筑之一,殿中央有 4 根同样大小的圆柱形“龙井柱”。“龙井柱”的高是 19.2m ,底面直径是 1.2m 。如果把每根“龙井柱”的表面(只包含侧面)刷一层油漆,那么粉刷的面积约是多少平方米 (得数保留一位小数)
4. 加工一个无盖的圆柱形容器,底面周长是18.84 dm,高是7 dm。做一个这样的容器,准备1.6 m 的材料够不够
5. 一个圆柱被截去 10 cm 后,圆柱的表面积减少了 62.8 cm (如下图),原来圆柱的表面积是多少平方厘米
第5课时 练习课(第3、4课时)
1. 填空。
(1)广告公司制作了一个底面直径是 1.2 m、高是2.5 m 的圆柱形灯箱。 在灯箱侧面张贴海报,最大可以张贴( )m 的海报。
(2)一个圆柱的底面半径是 5 cm,高是 12 cm。 如果把它的高减少 2cm ,那么表面积减少( ) cm 。
(1)一个底面直径是 4 cm、高是 5cm 的圆柱形木块,截成3 小段圆柱形木块后,表面积比原来增加( )cm 。
A. 37.68 B. 50.24 C. 62.8 D. 75.36
(2)如果一个圆柱的底面周长与高的比是π:1,那么垂直圆柱底面且过圆柱上、下底面圆心的截面是( )。
A. 长方形 B. 正方形 C. 圆 D. 梯形
3. 一个用塑料薄膜搭成的蔬菜大棚(如图),长 20 m,横截面是一个半径为 2 m 的半圆,搭成这个大棚至少需要塑料薄膜多少平方米 这个大棚的种植面积是多少平方米
4. 爸爸用铁皮做了一个圆柱形的储物桶,它的上底面留有一个直径是 20 cm 的圆口,做这个
5. 优优和妈妈在家做了一个蛋糕(如下图),优优要给这个蛋糕的表面部分涂上一层奶油(下底面不涂),涂奶油部分的面积是多少平方厘米
第6课时 圆柱的体积(1)
1. 动手操作,实验探究。
乐乐把一个高20cm、底面半径是10 cm的圆柱形木料平均分成16 份,然后拼成了一个近似的长方体,请你帮助乐乐完成下面的实验记录表。
探究圆柱体体积实验记录表
2. 小区里有一种圆柱形的垃圾桶,每个垃圾桶内部的底面直径是3d m,高是 6 dm。 一对这样的垃圾桶一共能装下体积是多少立方分米的垃圾
3. 下图中的圆柱与长方体的体积相等。这个圆柱的高是多少分米 (单位:dm)
4. 把一个底面半径是 6 cm 的圆柱切拼成一个近似的长方体后(如图),表面积增加了180 cm ,原来圆柱的体积是多少立方厘米
第7 课时 圆柱的体积(2)
1. 填空。
(1)将1.8 L果汁倒入内部底面半径是 3 cm、高是10 cm 的圆柱形玻璃杯中,最多能倒满( )杯。 (π取3)
(2)一个圆柱形水桶,从里面量,底面半径是2dm,高是5dm。 已知每立方分米水重1kg,这个水桶能盛水( ) kg。
2. 选择。
(1)新疆吐鲁番火焰山景区有一根世界上最大的圆柱形温度计,取名“金箍棒”。 它的直径是 0.65 m,高12 m,温度显示高5.4 m。 它的体积大约是( )m 。
A. 2 B. 4 C. 11 D. 24
(2)一根圆柱形输油管,内直径是2dm,油在管内的平均流速是4分米/秒,每秒流过的油的体积是( ) cm 。
A. 50240 B. 1256 C. 2512 D. 12560
(3)把一根长 1m 的圆柱形钢材截成两段后,表面积增加了 6.28 dm ,这根钢材原来的体积是( ) dm 。
A. 31.4 B. 3.14 C. 6.28 D. 62.8
3. 一管鞋油出口的直径为4mm,张叔叔每天擦皮鞋都挤出约 20mm长的鞋油,这管鞋油大约有多少毫升
4. 王老师家有一个长方体鱼缸,长、宽、高分别为 6 dm、3.5 dm、2.5 dm,鱼缸内水深2d m,鱼缸内的假山浸没在水中,体积为5dm 。换水时,把鱼缸里的水倒入一个圆柱形水桶内,已知水桶的底面积为 10 dm ,高为3.9 dm。 这个水桶能装下这些水吗 (鱼缸、水桶厚度忽略不计)
5. 公元前 13 世纪,凯尔特人从两河流域的人们那里学到了制桶手艺,开始使用木桶。世界上最早的洗衣机就是由木桶制作而成。一个底面直径是 4d m的圆柱形木桶,高 5 dm。这个木桶破损后(如图),最多能盛多少升水 (木桶厚度忽略不计)
第8课时 圆柱的体积(3)
1. 填空。
(1)一个水瓶,瓶身是圆柱形,内装有水 350 mL,将水瓶倒放时,空余部分的高度为5cm (如图)。这个水瓶的容积是( ) mL。
(2)如图,乌鸦将一块石子投到水瓶里,水面上升了0.1cm,这块石子的体积是( )cm 。若水面有 10 c m 高时,乌鸦就可以喝到甘甜可口的水,则乌鸦还需要再投到水瓶里( )块相同大小的石子。
2. 如图,一个内直径是 6 cm 的瓶里装满矿泉水,小兰喝了一些后,这时瓶里水的高度是
12 cm,把瓶盖拧紧后倒置放平,无水部分高 8cm 。小兰喝了多少毫升的水 这个瓶子的
4. 纪念品店加工一种艺术节比赛奖杯(如图)。加工时,一个有机玻璃圆柱正好可以截成两
5. 在一个圆柱形水桶里,垂直放入一根底面半径为5 cm 的圆柱形钢材。如果钢材浸没在水中,桶里的水就上升9 cm;如果让钢材露出 8 cm,这时桶里的水比钢材浸没在水中时低4 cm。这根钢材的体积是多少立方厘米
第9课时 练习课(第6~8课时)
1. 填空。
(1)一个圆柱的底面周长是 12.56 cm,高是 15 cm,这个圆柱的表面积是( ) cm ,体积是( ) cm 。
(2)一个圆柱的侧面积是 188.4 cm ,高是 10 cm,这个圆柱的体积是( ) cm 。
(3)一个圆柱的底面直径是4 cm,侧面展开图是正方形,这个圆柱的体积是( )cm 。
(4)圆柱的底面半径和高都扩大到原来的 2 倍,圆柱的体积扩大到原来的( )倍。
2. 选择。
(1)长方体、正方体和圆柱的体积都可以用“V=Sh”计算。下面图形( )的体积也可以用“V=Sh”计算。
(2)一块长 25.12cm、宽9.42 cm 的长方形铁皮,再配上两块直径是( ) cm 的圆形铁皮就可以做成一个容积最大的圆柱形容器。
A. 4 B. 1.5 C. 8 D. 3
3. 优优为了测量一个鸡蛋的体积,用一个底面直径是8cm 的圆柱形玻璃杯,做了如图实验。若实验中的各类误差忽略不计,则鸡蛋的体积是多少立方厘米
4. 工地运来了一根水泥管(如下图),管壁厚 2d m。这根水泥管用了多少立方米的水泥
5. 将一根底面直径是6 dm 的圆柱形木料,沿高切成形状、大小完全相同的两块后,表面积增加了 360 dm 。这根圆柱形木料的体积是多少立方分米
第1课时 圆柱的认识(1)
1. 填空。
(1)圆柱是由( )个面围成的。 圆柱的上、下两个面叫做( )。 圆柱周围的面(上、下底面除外)叫做( )。 圆柱的两个底面之间的距离叫做( ),圆柱有( )条高。
(2)下面的图形是圆柱的在括号里画“ ”,不是圆柱的画“×”。
2. 下面各图中h 表示的是圆柱的高吗 是的在括号里画“ ”,不是的画“×”。
3. 转动长方形ABCD,生成下面的两个圆柱。
(1)圆柱甲是以长方形的( )边所在的直线为轴旋转而成的,底面半径是( ),高是( )。
(2)圆柱乙是以长方形的( )边所在的直线为轴旋转而成的,底面半径是( ),高是( ) 。
4. 一个底面周长是9.42 cm、高是6 cm的圆柱,沿底面直径垂直把它切割成完全相同的两部分后,切割面的面积一共是多少平方厘米
第2课时 圆柱的认识(2)
1. 圆柱的侧面展开后可能是什么形状 (在可能的形状下面画“ ”)
2. 填空。
(1)一个圆柱的底面半径是3cm,高是5cm,它的侧面展开图是一个长方形。这个长方形的长是( ) cm,宽是( ) cm。
(2)一个圆柱的侧面展开图是一个正方形,这个圆柱的高是 25.12 dm,那么圆柱的底面周长是( ) dm,底面直径是( ) dm。
3. 选择。
(1)如果圆柱的底面直径和高相等,那么圆柱的侧面沿高展开一定是( )。
A. 平行四边形 B. 等腰梯形 C. 正方形 D. 长方形(长、宽不相等)
(2)下面的图形是圆柱展开图的是( )。(单位:cm)
4. 一个圆柱的侧面展开图是一个长 31.4 cm、宽 12.56 cm 的长方形,求这个圆柱的底面半径。
5. 把一张长方形纸片按如图所示方法剪开后,正好可以做成一个圆柱,做成的圆柱的底面直径和底面周长分别是多少分米
第3课时 圆柱的表面积(1)
1. 填空。
(1)一个圆柱的侧面积是 9.42 cm ,底面积是 3.14 cm ,它的表面积是( )cm 。
(2)一个圆柱的侧面展开图是一个长 5.2 cm、宽 4 cm 的长方形,这个圆柱的侧面积是( )cm 。
2. 选择。
(1)做一个无盖的圆柱形水桶,求至少需要多少铁皮,就是求圆柱的( )。
A. 底面积 B. 侧面积 C. 表面积 D. 侧面积+一个底面积
(2)一个圆柱的侧面积是 25.12 dm ,底面周长是 3.14 dm,它的高是( )。
A. 2 dm B. 4 dm C. 8 dm D. 16 dm
3. 计算下面各圆柱的表面积。
4. 下图是一张长方形纸,长 12 cm,宽 10 cm。如果以长边所在的直线为轴旋转一周得到一个圆柱,那么圆柱的表面积是多少平方厘米
5. 用下面的长方形纸片刚好围成一个底面半径是 1 cm 的圆柱的侧面(不考虑接头处),这个圆柱的侧面积是多少平方厘米
6. 如图,在一张长方形纸上,剪下阴影部分可围成一个圆柱,求这个圆柱的表面积。
第4课时 圆柱的表面积(2)
1. 填空。
(1)做一个圆柱形封闭式铁皮油桶,高 18 dm,底面直径是高的 / ,至少需要( )dm 铁皮。(得数保留整数)
(1)用铁皮制作 5 节通风管,每节长1m,底面半径是 10 cm,至少需要( )m 的铁皮。
A. 0.628 B. 3.14 C. 6.28 D. 31.4
(2)一个圆柱的侧面展开图是一个正方形。这个圆柱底面直径与高的比是( )。
A. 1 : π B. 1 ∶ 2π C. 1∶4π D. 2: π
3. 祈年殿是北京天坛公园的主要建筑之一,殿中央有 4 根同样大小的圆柱形“龙井柱”。“龙井柱”的高是 19.2m ,底面直径是 1.2m 。如果把每根“龙井柱”的表面(只包含侧面)刷一层油漆,那么粉刷的面积约是多少平方米 (得数保留一位小数)
4. 加工一个无盖的圆柱形容器,底面周长是18.84 dm,高是7 dm。做一个这样的容器,准备1.6 m 的材料够不够
5. 一个圆柱被截去 10 cm 后,圆柱的表面积减少了 62.8 cm (如下图),原来圆柱的表面积是多少平方厘米
第5课时 练习课(第3、4课时)
1. 填空。
(1)广告公司制作了一个底面直径是 1.2 m、高是2.5 m 的圆柱形灯箱。 在灯箱侧面张贴海报,最大可以张贴( )m 的海报。
(2)一个圆柱的底面半径是 5 cm,高是 12 cm。 如果把它的高减少 2cm ,那么表面积减少( ) cm 。
(1)一个底面直径是 4 cm、高是 5cm 的圆柱形木块,截成3 小段圆柱形木块后,表面积比原来增加( )cm 。
A. 37.68 B. 50.24 C. 62.8 D. 75.36
(2)如果一个圆柱的底面周长与高的比是π:1,那么垂直圆柱底面且过圆柱上、下底面圆心的截面是( )。
A. 长方形 B. 正方形 C. 圆 D. 梯形
3. 一个用塑料薄膜搭成的蔬菜大棚(如图),长 20 m,横截面是一个半径为 2 m 的半圆,搭成这个大棚至少需要塑料薄膜多少平方米 这个大棚的种植面积是多少平方米
4. 爸爸用铁皮做了一个圆柱形的储物桶,它的上底面留有一个直径是 20 cm 的圆口,做这个
5. 优优和妈妈在家做了一个蛋糕(如下图),优优要给这个蛋糕的表面部分涂上一层奶油(下底面不涂),涂奶油部分的面积是多少平方厘米
第6课时 圆柱的体积(1)
1. 动手操作,实验探究。
乐乐把一个高20cm、底面半径是10 cm的圆柱形木料平均分成16 份,然后拼成了一个近似的长方体,请你帮助乐乐完成下面的实验记录表。
探究圆柱体体积实验记录表
2. 小区里有一种圆柱形的垃圾桶,每个垃圾桶内部的底面直径是3d m,高是 6 dm。 一对这样的垃圾桶一共能装下体积是多少立方分米的垃圾
3. 下图中的圆柱与长方体的体积相等。这个圆柱的高是多少分米 (单位:dm)
4. 把一个底面半径是 6 cm 的圆柱切拼成一个近似的长方体后(如图),表面积增加了180 cm ,原来圆柱的体积是多少立方厘米
第7 课时 圆柱的体积(2)
1. 填空。
(1)将1.8 L果汁倒入内部底面半径是 3 cm、高是10 cm 的圆柱形玻璃杯中,最多能倒满( )杯。 (π取3)
(2)一个圆柱形水桶,从里面量,底面半径是2dm,高是5dm。 已知每立方分米水重1kg,这个水桶能盛水( ) kg。
2. 选择。
(1)新疆吐鲁番火焰山景区有一根世界上最大的圆柱形温度计,取名“金箍棒”。 它的直径是 0.65 m,高12 m,温度显示高5.4 m。 它的体积大约是( )m 。
A. 2 B. 4 C. 11 D. 24
(2)一根圆柱形输油管,内直径是2dm,油在管内的平均流速是4分米/秒,每秒流过的油的体积是( ) cm 。
A. 50240 B. 1256 C. 2512 D. 12560
(3)把一根长 1m 的圆柱形钢材截成两段后,表面积增加了 6.28 dm ,这根钢材原来的体积是( ) dm 。
A. 31.4 B. 3.14 C. 6.28 D. 62.8
3. 一管鞋油出口的直径为4mm,张叔叔每天擦皮鞋都挤出约 20mm长的鞋油,这管鞋油大约有多少毫升
4. 王老师家有一个长方体鱼缸,长、宽、高分别为 6 dm、3.5 dm、2.5 dm,鱼缸内水深2d m,鱼缸内的假山浸没在水中,体积为5dm 。换水时,把鱼缸里的水倒入一个圆柱形水桶内,已知水桶的底面积为 10 dm ,高为3.9 dm。 这个水桶能装下这些水吗 (鱼缸、水桶厚度忽略不计)
5. 公元前 13 世纪,凯尔特人从两河流域的人们那里学到了制桶手艺,开始使用木桶。世界上最早的洗衣机就是由木桶制作而成。一个底面直径是 4d m的圆柱形木桶,高 5 dm。这个木桶破损后(如图),最多能盛多少升水 (木桶厚度忽略不计)
第8课时 圆柱的体积(3)
1. 填空。
(1)一个水瓶,瓶身是圆柱形,内装有水 350 mL,将水瓶倒放时,空余部分的高度为5cm (如图)。这个水瓶的容积是( ) mL。
(2)如图,乌鸦将一块石子投到水瓶里,水面上升了0.1cm,这块石子的体积是( )cm 。若水面有 10 c m 高时,乌鸦就可以喝到甘甜可口的水,则乌鸦还需要再投到水瓶里( )块相同大小的石子。
2. 如图,一个内直径是 6 cm 的瓶里装满矿泉水,小兰喝了一些后,这时瓶里水的高度是
12 cm,把瓶盖拧紧后倒置放平,无水部分高 8cm 。小兰喝了多少毫升的水 这个瓶子的
4. 纪念品店加工一种艺术节比赛奖杯(如图)。加工时,一个有机玻璃圆柱正好可以截成两
5. 在一个圆柱形水桶里,垂直放入一根底面半径为5 cm 的圆柱形钢材。如果钢材浸没在水中,桶里的水就上升9 cm;如果让钢材露出 8 cm,这时桶里的水比钢材浸没在水中时低4 cm。这根钢材的体积是多少立方厘米
第9课时 练习课(第6~8课时)
1. 填空。
(1)一个圆柱的底面周长是 12.56 cm,高是 15 cm,这个圆柱的表面积是( ) cm ,体积是( ) cm 。
(2)一个圆柱的侧面积是 188.4 cm ,高是 10 cm,这个圆柱的体积是( ) cm 。
(3)一个圆柱的底面直径是4 cm,侧面展开图是正方形,这个圆柱的体积是( )cm 。
(4)圆柱的底面半径和高都扩大到原来的 2 倍,圆柱的体积扩大到原来的( )倍。
2. 选择。
(1)长方体、正方体和圆柱的体积都可以用“V=Sh”计算。下面图形( )的体积也可以用“V=Sh”计算。
(2)一块长 25.12cm、宽9.42 cm 的长方形铁皮,再配上两块直径是( ) cm 的圆形铁皮就可以做成一个容积最大的圆柱形容器。
A. 4 B. 1.5 C. 8 D. 3
3. 优优为了测量一个鸡蛋的体积,用一个底面直径是8cm 的圆柱形玻璃杯,做了如图实验。若实验中的各类误差忽略不计,则鸡蛋的体积是多少立方厘米
4. 工地运来了一根水泥管(如下图),管壁厚 2d m。这根水泥管用了多少立方米的水泥
5. 将一根底面直径是6 dm 的圆柱形木料,沿高切成形状、大小完全相同的两块后,表面积增加了 360 dm 。这根圆柱形木料的体积是多少立方分米
