7.1.2 平面直角坐标系课件 (共36张PPT)
文档属性
| 名称 | 7.1.2 平面直角坐标系课件 (共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:35:11 | ||
图片预览





文档简介
(共36张PPT)
7.1.2 平面直角坐标系
七年级下
人教版
1. 理解平面直角坐标系的有关概念,能画出平面直角坐标系.
2. 在给定的平面直角坐标系中,能根据坐标描出点的位置,由点的位置写出坐标.
3. 知道象限分布以及象限内、坐标轴上的点的特征.
4.对给定的正方形,会选择合适的平面直角坐标系,写出它的顶点坐标,体会可以用坐标表达简单图形.
学习目标
重点
难点
重点
难点
新课引入
实数与数轴上的点有怎样的关系?
数轴上的点与实数是一一对应的:
数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标;
反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.
0
1
2
3
4
3
2
1
A
B
C
0
1
2
3
4
3
2
1
A
B
C
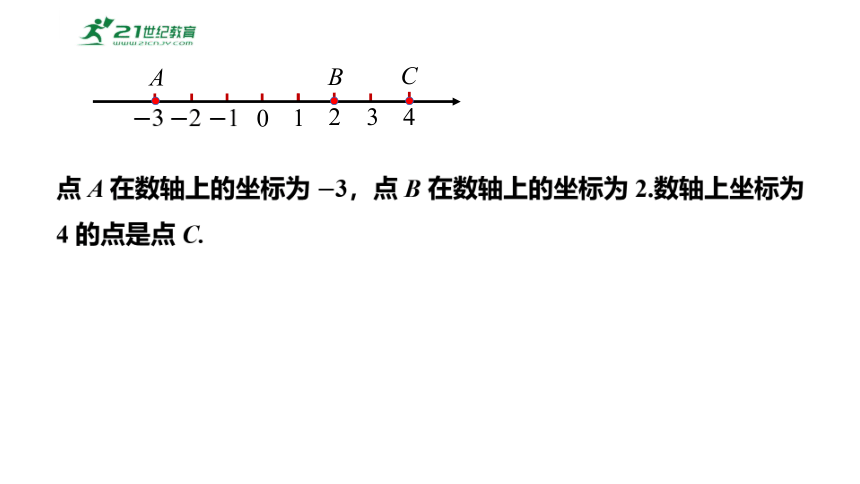
点 A 在数轴上的坐标为 3,点 B 在数轴上的坐标为 2.数轴上坐标为 4 的点是点 C.
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢(如下图中的A、B、C、D各点)?
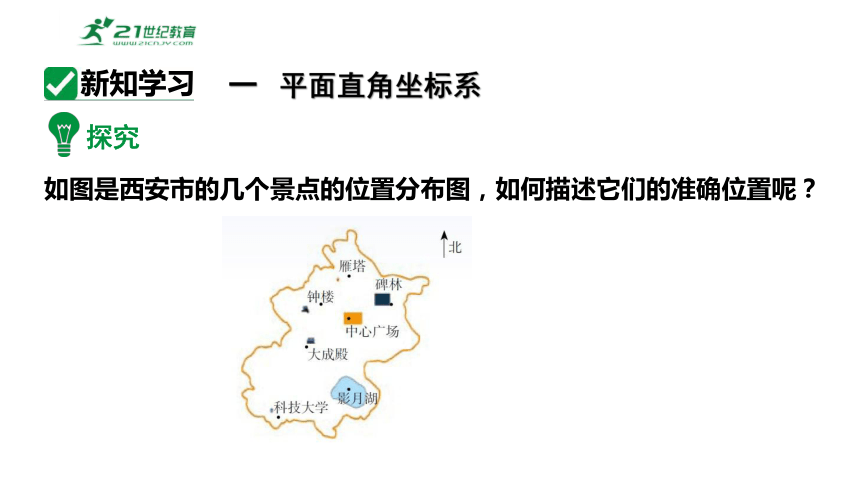
如图是西安市的几个景点的位置分布图,如何描述它们的准确位置呢?
探究
新知学面直角坐标系
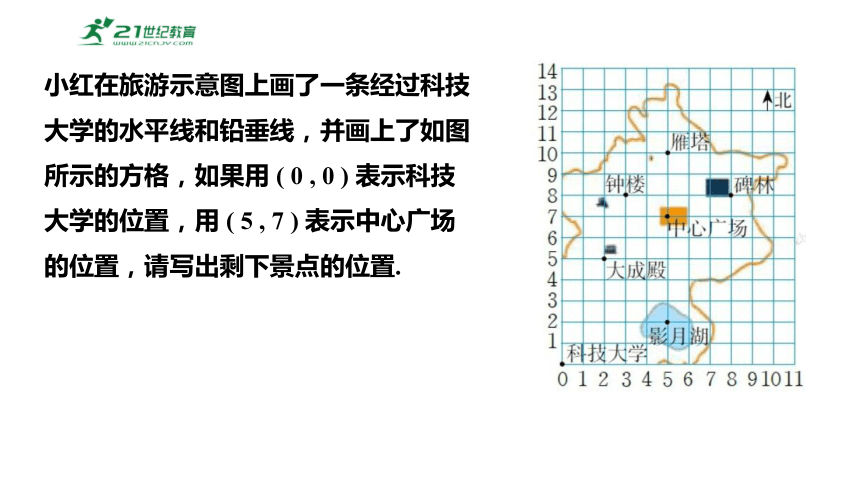
小红在旅游示意图上画了一条经过科技大学的水平线和铅垂线,并画上了如图所示的方格,如果用 ( 0 , 0 ) 表示科技大学的位置,用 ( 5 , 7 ) 表示中心广场的位置,请写出剩下景点的位置.
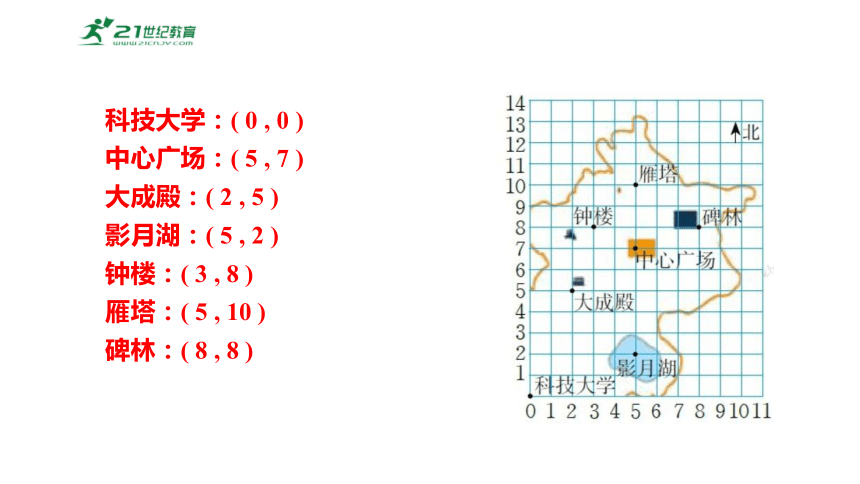
科技大学:( 0 , 0 )
中心广场:( 5 , 7 )
大成殿:( 2 , 5 )
影月湖:( 5 , 2 )
钟楼:( 3 , 8 )
雁塔:( 5 , 10 )
碑林:( 8 , 8 )
小亮画了如图所示的图形:
(1) 把经过中心广场的水平线记作 x 轴,并规定向右为正,向左为负;
(2) 把经过中心广场的铅垂线记作 y 轴,规定向上为正,向下为负,并画上了如图所示的方格.
你能用有序数对表示每个景点吗?
中心广场
碑林
雁塔
钟楼
大成殿
科技大学
影月楼
(0, 0)
(3, 1)
(0, 3)
(-2, 1)
(-3,-2)
(-5,-7)
(0,-5)
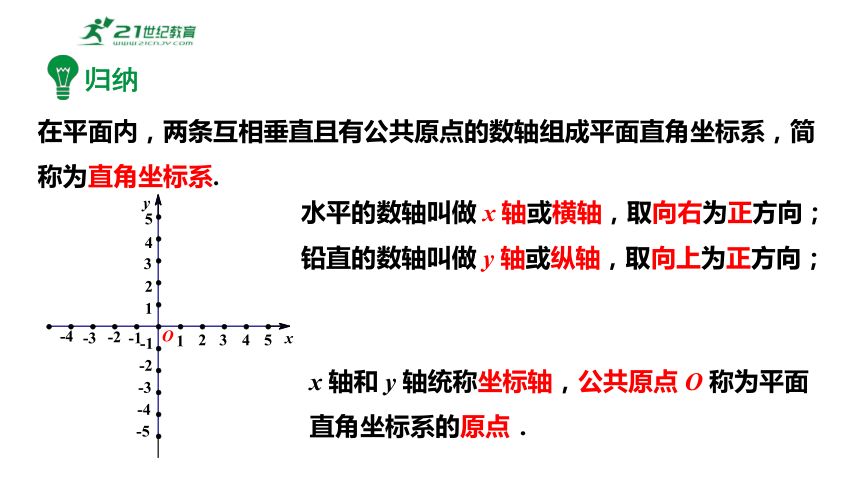
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,简称为直角坐标系.
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
水平的数轴叫做 x 轴或横轴,取向右为正方向;
铅直的数轴叫做 y 轴或纵轴,取向上为正方向;
x 轴和 y 轴统称坐标轴,公共原点 O 称为平面直角坐标系的原点.
归纳
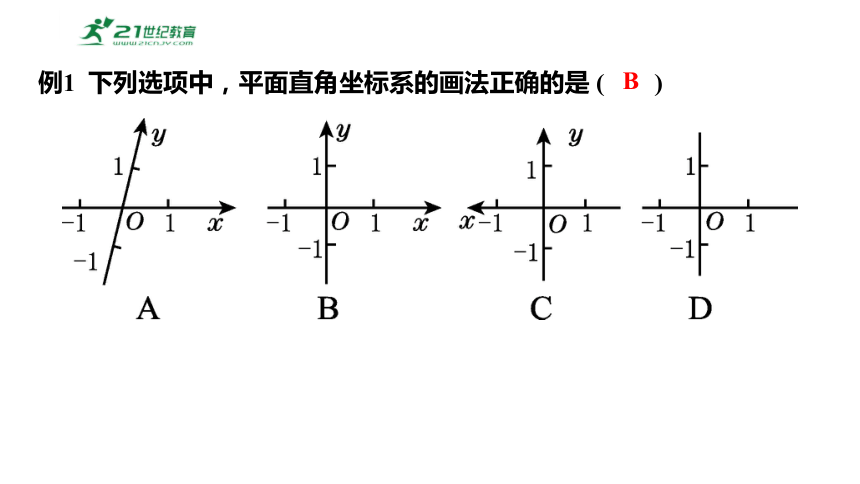
例1 下列选项中,平面直角坐标系的画法正确的是 ( )
B
x
y
x
y
x
y
归纳
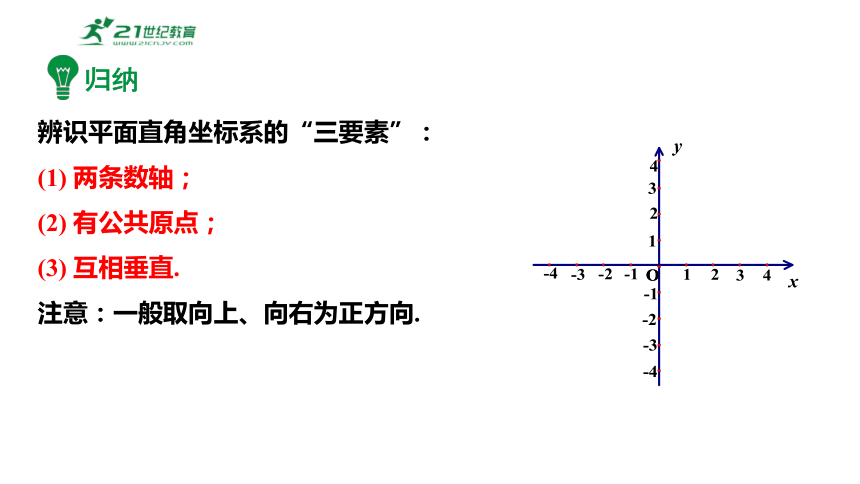
辨识平面直角坐标系的“三要素”:
(1) 两条数轴;
(2) 有公共原点;
(3) 互相垂直.
注意:一般取向上、向右为正方向.
早在 1637 年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线,所以笛卡尔的方法就是在平面内画两条原点重合,互相垂直且具有相同单位长度的数轴建立直角坐标系,从而解决了用一对实数表示平面内点的位置的问题.
扩展
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了.
规定把横坐标写在前,纵坐标写在后
x
O
y
1 2 3 4
4321
4
3
2
1
1
2
3
4
M
N
如图,由点 A 分别向 x 轴和 y 轴作垂线,垂足 M 在 x 轴上的坐标是 3,垂足 N 在 y 轴上的坐标是 4,我们说点 A 的横坐标是 3,纵坐标是 4,有序数对 (3,4) 就叫做点 A 的坐标,记作 A (3,4).
类似地,请你写出点 B,C,D的坐标:
B (___,____)
C (___,____)
D (___,____)
x
O
y
1 2 3 4
4321
4
3
2
1
1
2
3
4
-3
-4
0
2
0
-3
例2 写出多边形 ABCDEF 各个顶点的坐标.
F
A
B
C
D
E
解:各个顶点的坐标分别为:
A ( -2 , 0 ) B( 0 , -3 )
C ( 4 , -3 ) D( 5 , 0 )
E ( 4 , 3 ) F( 0 , 3 )
建立了平面直角坐标系后,坐标平面就被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限、第四象限.
坐标轴上的点不属于任何象限!
y
o
-1
2
3
4
5
-2
-3
-4
-5
-6
1
1
2
3
4
5
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
二 直角坐标系中点的坐标的特征
观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
探究
y
o
-1
2
3
4
5
-2
-3
-4
-5
-6
1
1
2
3
4
5
-1
-2
-3
-4
x
第一象限
第二象限
第四象限
第三象限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
探究
在平面直角坐标系中,描出下列各点:
A(3, 4),B(3, -2) ,C(1, 2),D(-2, 2),
A
B
C
D
点A和点B坐标有什么特征?
点C和点D坐标有什么特征?
1.平行于横轴的直线上的点,纵坐标相同;
2.平行于纵轴的直线上的点,横坐标相同;
E
F
点E和点F坐标有什么特征?
点G和点H坐标有什么特征?
1.横轴(x轴)上的点纵坐标为0;
2.纵轴(y轴)上的点横坐标为0.
探究
在平面直角坐标系中,描出下列各点:
E(2, 0),F(-3, 0) ,G(0, -3),H(0, 2),
G
H
归纳
1.平行于横轴的直线上的点,纵坐标相同;
2.平行于纵轴的直线上的点,横坐标相同;
3.横轴(x轴)上的点,纵坐标为0;
4.纵轴(y轴)上的点,横坐标为0.
例3 在直角坐标系中,描出下列各点的位置:
A(4 , 5),B( -2 , 3),C( -4 , -1),D(2.5 , -2),E(0 , -4).
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
x
A
(4 , 5)
解:如图,先在轴上找出表示4的点;再在y轴上找出表示5的点;过这两个点分别作轴和y轴的垂线,垂线的交点就是点A.
例3 在直角坐标系中,描出下列各点的位置:
A(4 , 5),B( -2 , 3),C( -4 , -1),D(2.5 , -2),E(0 , -4).
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
x
E
(0 , -4)
C
(-4 , -1)
A
(4 , 5)
B
(-2 , 3)
D
(2.5 , -2)
类似地,就可以在坐标系中描出点B、C、D、E.
归纳
已知坐标描点的方法
(1) 先在坐标轴上找到表示横坐标与纵坐标的点;
(2) 然后过这两点分别作轴与轴的垂线;
(3) 垂线的交点就是该坐标对应的点.
归纳
我们知道,数轴上的点与实数是一一对应的.我们还可以得出:对于坐标平面内任意一点 M,都有唯一的一对有序实数 (x,y) (即点 M 的坐标) 和它对应;反过来,对于任意一对有序实数 (x,y) ,在坐标平面内都有唯一的一点 M (即坐标为 (x,y) 的点) 和它对应.也就是说,坐标平面内的点与有序数对是一一对应的.
如图,正方形 ABCD 的边长为6,如果以点 A 为原点,AB 所在直线为 x 轴,建立平面直角坐标系,那么y 轴是哪条线? 写出正方形的顶点 A,B,C,D 的坐标.
探究
6
6
y
x
(A)
B
C
D
O
AD 所在直线为 y 轴,
A(0,0),B(6,0),C(6,6), D(0,6).
请另建立一个平面直角坐标系,这时正方形的顶点 A,B,C,D 的坐标又分别是什么?
6
6
y
x
A
B
C
(D)
O
解法1:如图,以顶点 D 为原点,DC 所在直线为 x 轴,AD 所在直线为 y 轴建立平面直角坐标系.
此时, A,B,C,D 的坐标分别为:
A(0,-6),B(6,-6),C(6,0),D(0,0).
解法2:如图,以顶点 C 为原点,DC 所在直线为 x 轴,BC 所在直线为 y 轴建立平面直角坐标系.
6
6
y
x
A
B
(C)
D
O
此时, A,B,C,D 的坐标分别为:
A(-6,-6),B(0, -6),C(0, 0),D(-6, 0).
解法3:如图,以顶点 B 为原点,AB 所在直线为 x 轴,BC 所在直线为 y 轴建立平面直角坐标系.
6
6
y
x
A
(B)
C
D
O
此时, A,B,C,D 的坐标分别为:
A(-6,0),B(0,0),C(0,6),D(-6,4).
解法4:如图,以正方形 ABCD 的中心为原点,过中心平行于 AB 的直线为 x 轴,过中心平行于 AD 的直线为 y 轴建立平面直角坐标系.
3
3
y
x
A
B
C
D
O
3
3
此时, A,B,C,D 的坐标分别为:
A(-3,-3),B(3,-3),C(3, 3),D(-3, 3).
几何图形中建立适当的平面直角坐标系的技巧
1. 使图形中尽量多的点在坐标轴上;
2. 以某些特殊线段所在的直线为 x 轴或 y 轴;
3. 若图形被一条直线分得的两部分形状、大小相同,则可以将此直线作为 x 轴或 y 轴;
4. 以某已知点为原点,使它的坐标为(0,0).
归纳
1. 判断:
(1) 对于坐标平面内的任一点,都有唯一的一对有序实数与它对应. ( )
(2) 在直角坐标系内,原点的坐标是 0. ( )
(3) 点 A(a , -b) 在第二象限,则点 B(-a , b) 在第四象限. ( )
(4) 若点 P 的坐标为 (a , b),且 a·b = 0,则点 P 一定在坐标原点. ( )
√
√
×
×
随堂练习
2. 点 A ( 3 , -2 ) 在第_______象限;点 B( -5 , 2 ) 在第_______象限.
3. 已知 P ( 3 , -2 ),则 P 点到 x 轴的距离为_______,到 y 轴的距离为_______.
4. 点 M ( x , y )在第四象限且 x2 = 9,y2 = 16,则 M 点的坐标为_______.
四
二
2
3
( 3 , -4 )
5. 下图是学校的示意图,如图,以办公楼所在位置为原点建立平面直角坐标系.
(1) 请写出教学楼、实验楼、图书馆的坐标;
(2) 学校准备在 ( -3 , -3 ) 处建一栋学生公寓,请你标出学生公寓的位置.
答案∶
(1) 教学楼 ( 2 , 4 ),实验楼( 3 , -3 ),图书馆 ( -3 , 3 );
x
y
O
1
学生公寓
1
6.在直角坐标系中,描出下列各点的位置:
A(4 , 1),B( -1 , 4),C( -4 , -2),D(3 , -2),E(0 , 1),F(-4 , 0) .
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
x
E
(0 , 1)
C
(-4 , -2)
A
(4 , 1)
B
(-1 , 4)
F
(-4 , 0)
D
(3 , -2)
平面直角
坐标系
x 轴和 y 轴把坐标平面分成四个部分,分别叫做第一、
二、三、四象限;
坐标平面内点的坐标特征;
点与有序实数对的对应关系:
平面直角坐
标系内点的
坐标特征
平面直角
坐标系
水平的数轴叫做x 轴或横轴,取向右为正方向
垂直的数轴叫做y 轴或纵轴,取向上为正方向
两轴交点 O 为原点
点
有序数对
一一对应
课堂小结
7.1.2 平面直角坐标系
七年级下
人教版
1. 理解平面直角坐标系的有关概念,能画出平面直角坐标系.
2. 在给定的平面直角坐标系中,能根据坐标描出点的位置,由点的位置写出坐标.
3. 知道象限分布以及象限内、坐标轴上的点的特征.
4.对给定的正方形,会选择合适的平面直角坐标系,写出它的顶点坐标,体会可以用坐标表达简单图形.
学习目标
重点
难点
重点
难点
新课引入
实数与数轴上的点有怎样的关系?
数轴上的点与实数是一一对应的:
数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标;
反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.
0
1
2
3
4
3
2
1
A
B
C
0
1
2
3
4
3
2
1
A
B
C
点 A 在数轴上的坐标为 3,点 B 在数轴上的坐标为 2.数轴上坐标为 4 的点是点 C.
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢(如下图中的A、B、C、D各点)?
如图是西安市的几个景点的位置分布图,如何描述它们的准确位置呢?
探究
新知学面直角坐标系
小红在旅游示意图上画了一条经过科技大学的水平线和铅垂线,并画上了如图所示的方格,如果用 ( 0 , 0 ) 表示科技大学的位置,用 ( 5 , 7 ) 表示中心广场的位置,请写出剩下景点的位置.
科技大学:( 0 , 0 )
中心广场:( 5 , 7 )
大成殿:( 2 , 5 )
影月湖:( 5 , 2 )
钟楼:( 3 , 8 )
雁塔:( 5 , 10 )
碑林:( 8 , 8 )
小亮画了如图所示的图形:
(1) 把经过中心广场的水平线记作 x 轴,并规定向右为正,向左为负;
(2) 把经过中心广场的铅垂线记作 y 轴,规定向上为正,向下为负,并画上了如图所示的方格.
你能用有序数对表示每个景点吗?
中心广场
碑林
雁塔
钟楼
大成殿
科技大学
影月楼
(0, 0)
(3, 1)
(0, 3)
(-2, 1)
(-3,-2)
(-5,-7)
(0,-5)
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,简称为直角坐标系.
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
水平的数轴叫做 x 轴或横轴,取向右为正方向;
铅直的数轴叫做 y 轴或纵轴,取向上为正方向;
x 轴和 y 轴统称坐标轴,公共原点 O 称为平面直角坐标系的原点.
归纳
例1 下列选项中,平面直角坐标系的画法正确的是 ( )
B
x
y
x
y
x
y
归纳
辨识平面直角坐标系的“三要素”:
(1) 两条数轴;
(2) 有公共原点;
(3) 互相垂直.
注意:一般取向上、向右为正方向.
早在 1637 年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线,所以笛卡尔的方法就是在平面内画两条原点重合,互相垂直且具有相同单位长度的数轴建立直角坐标系,从而解决了用一对实数表示平面内点的位置的问题.
扩展
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了.
规定把横坐标写在前,纵坐标写在后
x
O
y
1 2 3 4
4321
4
3
2
1
1
2
3
4
M
N
如图,由点 A 分别向 x 轴和 y 轴作垂线,垂足 M 在 x 轴上的坐标是 3,垂足 N 在 y 轴上的坐标是 4,我们说点 A 的横坐标是 3,纵坐标是 4,有序数对 (3,4) 就叫做点 A 的坐标,记作 A (3,4).
类似地,请你写出点 B,C,D的坐标:
B (___,____)
C (___,____)
D (___,____)
x
O
y
1 2 3 4
4321
4
3
2
1
1
2
3
4
-3
-4
0
2
0
-3
例2 写出多边形 ABCDEF 各个顶点的坐标.
F
A
B
C
D
E
解:各个顶点的坐标分别为:
A ( -2 , 0 ) B( 0 , -3 )
C ( 4 , -3 ) D( 5 , 0 )
E ( 4 , 3 ) F( 0 , 3 )
建立了平面直角坐标系后,坐标平面就被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限、第四象限.
坐标轴上的点不属于任何象限!
y
o
-1
2
3
4
5
-2
-3
-4
-5
-6
1
1
2
3
4
5
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
二 直角坐标系中点的坐标的特征
观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
探究
y
o
-1
2
3
4
5
-2
-3
-4
-5
-6
1
1
2
3
4
5
-1
-2
-3
-4
x
第一象限
第二象限
第四象限
第三象限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
探究
在平面直角坐标系中,描出下列各点:
A(3, 4),B(3, -2) ,C(1, 2),D(-2, 2),
A
B
C
D
点A和点B坐标有什么特征?
点C和点D坐标有什么特征?
1.平行于横轴的直线上的点,纵坐标相同;
2.平行于纵轴的直线上的点,横坐标相同;
E
F
点E和点F坐标有什么特征?
点G和点H坐标有什么特征?
1.横轴(x轴)上的点纵坐标为0;
2.纵轴(y轴)上的点横坐标为0.
探究
在平面直角坐标系中,描出下列各点:
E(2, 0),F(-3, 0) ,G(0, -3),H(0, 2),
G
H
归纳
1.平行于横轴的直线上的点,纵坐标相同;
2.平行于纵轴的直线上的点,横坐标相同;
3.横轴(x轴)上的点,纵坐标为0;
4.纵轴(y轴)上的点,横坐标为0.
例3 在直角坐标系中,描出下列各点的位置:
A(4 , 5),B( -2 , 3),C( -4 , -1),D(2.5 , -2),E(0 , -4).
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
x
A
(4 , 5)
解:如图,先在轴上找出表示4的点;再在y轴上找出表示5的点;过这两个点分别作轴和y轴的垂线,垂线的交点就是点A.
例3 在直角坐标系中,描出下列各点的位置:
A(4 , 5),B( -2 , 3),C( -4 , -1),D(2.5 , -2),E(0 , -4).
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
x
E
(0 , -4)
C
(-4 , -1)
A
(4 , 5)
B
(-2 , 3)
D
(2.5 , -2)
类似地,就可以在坐标系中描出点B、C、D、E.
归纳
已知坐标描点的方法
(1) 先在坐标轴上找到表示横坐标与纵坐标的点;
(2) 然后过这两点分别作轴与轴的垂线;
(3) 垂线的交点就是该坐标对应的点.
归纳
我们知道,数轴上的点与实数是一一对应的.我们还可以得出:对于坐标平面内任意一点 M,都有唯一的一对有序实数 (x,y) (即点 M 的坐标) 和它对应;反过来,对于任意一对有序实数 (x,y) ,在坐标平面内都有唯一的一点 M (即坐标为 (x,y) 的点) 和它对应.也就是说,坐标平面内的点与有序数对是一一对应的.
如图,正方形 ABCD 的边长为6,如果以点 A 为原点,AB 所在直线为 x 轴,建立平面直角坐标系,那么y 轴是哪条线? 写出正方形的顶点 A,B,C,D 的坐标.
探究
6
6
y
x
(A)
B
C
D
O
AD 所在直线为 y 轴,
A(0,0),B(6,0),C(6,6), D(0,6).
请另建立一个平面直角坐标系,这时正方形的顶点 A,B,C,D 的坐标又分别是什么?
6
6
y
x
A
B
C
(D)
O
解法1:如图,以顶点 D 为原点,DC 所在直线为 x 轴,AD 所在直线为 y 轴建立平面直角坐标系.
此时, A,B,C,D 的坐标分别为:
A(0,-6),B(6,-6),C(6,0),D(0,0).
解法2:如图,以顶点 C 为原点,DC 所在直线为 x 轴,BC 所在直线为 y 轴建立平面直角坐标系.
6
6
y
x
A
B
(C)
D
O
此时, A,B,C,D 的坐标分别为:
A(-6,-6),B(0, -6),C(0, 0),D(-6, 0).
解法3:如图,以顶点 B 为原点,AB 所在直线为 x 轴,BC 所在直线为 y 轴建立平面直角坐标系.
6
6
y
x
A
(B)
C
D
O
此时, A,B,C,D 的坐标分别为:
A(-6,0),B(0,0),C(0,6),D(-6,4).
解法4:如图,以正方形 ABCD 的中心为原点,过中心平行于 AB 的直线为 x 轴,过中心平行于 AD 的直线为 y 轴建立平面直角坐标系.
3
3
y
x
A
B
C
D
O
3
3
此时, A,B,C,D 的坐标分别为:
A(-3,-3),B(3,-3),C(3, 3),D(-3, 3).
几何图形中建立适当的平面直角坐标系的技巧
1. 使图形中尽量多的点在坐标轴上;
2. 以某些特殊线段所在的直线为 x 轴或 y 轴;
3. 若图形被一条直线分得的两部分形状、大小相同,则可以将此直线作为 x 轴或 y 轴;
4. 以某已知点为原点,使它的坐标为(0,0).
归纳
1. 判断:
(1) 对于坐标平面内的任一点,都有唯一的一对有序实数与它对应. ( )
(2) 在直角坐标系内,原点的坐标是 0. ( )
(3) 点 A(a , -b) 在第二象限,则点 B(-a , b) 在第四象限. ( )
(4) 若点 P 的坐标为 (a , b),且 a·b = 0,则点 P 一定在坐标原点. ( )
√
√
×
×
随堂练习
2. 点 A ( 3 , -2 ) 在第_______象限;点 B( -5 , 2 ) 在第_______象限.
3. 已知 P ( 3 , -2 ),则 P 点到 x 轴的距离为_______,到 y 轴的距离为_______.
4. 点 M ( x , y )在第四象限且 x2 = 9,y2 = 16,则 M 点的坐标为_______.
四
二
2
3
( 3 , -4 )
5. 下图是学校的示意图,如图,以办公楼所在位置为原点建立平面直角坐标系.
(1) 请写出教学楼、实验楼、图书馆的坐标;
(2) 学校准备在 ( -3 , -3 ) 处建一栋学生公寓,请你标出学生公寓的位置.
答案∶
(1) 教学楼 ( 2 , 4 ),实验楼( 3 , -3 ),图书馆 ( -3 , 3 );
x
y
O
1
学生公寓
1
6.在直角坐标系中,描出下列各点的位置:
A(4 , 1),B( -1 , 4),C( -4 , -2),D(3 , -2),E(0 , 1),F(-4 , 0) .
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
x
E
(0 , 1)
C
(-4 , -2)
A
(4 , 1)
B
(-1 , 4)
F
(-4 , 0)
D
(3 , -2)
平面直角
坐标系
x 轴和 y 轴把坐标平面分成四个部分,分别叫做第一、
二、三、四象限;
坐标平面内点的坐标特征;
点与有序实数对的对应关系:
平面直角坐
标系内点的
坐标特征
平面直角
坐标系
水平的数轴叫做x 轴或横轴,取向右为正方向
垂直的数轴叫做y 轴或纵轴,取向上为正方向
两轴交点 O 为原点
点
有序数对
一一对应
课堂小结
