7.2.2 用坐标表示平移课件(共25张PPT)
文档属性
| 名称 | 7.2.2 用坐标表示平移课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 967.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
七年级下
人教版
7.2.2 用坐标表示平移
1.在平面直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移一定距离后图形的顶点坐标,知道对应顶点坐标之间的关系.
2.在平面直角坐标系中,探索并了解将一个多边形依次沿两个坐标轴方向平移后所得到的图形和原来图形具有平移关系,体会图形顶点坐标的变化.
学习目标
重点
难点
1. 什么叫平移?
3 .平移后得到的新图形与原图形有什么关系?
在平面内,把一个图形整体沿某一方向移动一定的距离,这种图形的变换叫做平移.
2.平移的要素是什么?
平移的方向、平移的距离
①平移只改变图形的位置,形状和大小不变.
②对应点的连线互相平行(或在同一条直线上)且相等.
新课引入
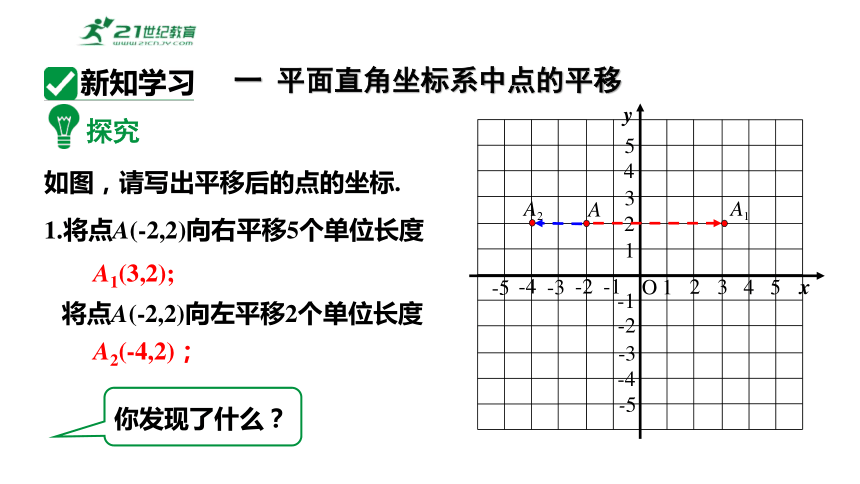
探究
1.将点A(-2,2)向右平移5个单位长度
如图,请写出平移后的点的坐标.
1
3
5
2
4
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-5
1
A1
A2
y
x
A
A1(3,2);
将点A(-2,2)向左平移2个单位长度
A2(-4,2);
你发现了什么?
新知学面直角坐标系中点的平移
1
3
5
2
4
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-5
1
A4
y
x
A
A3
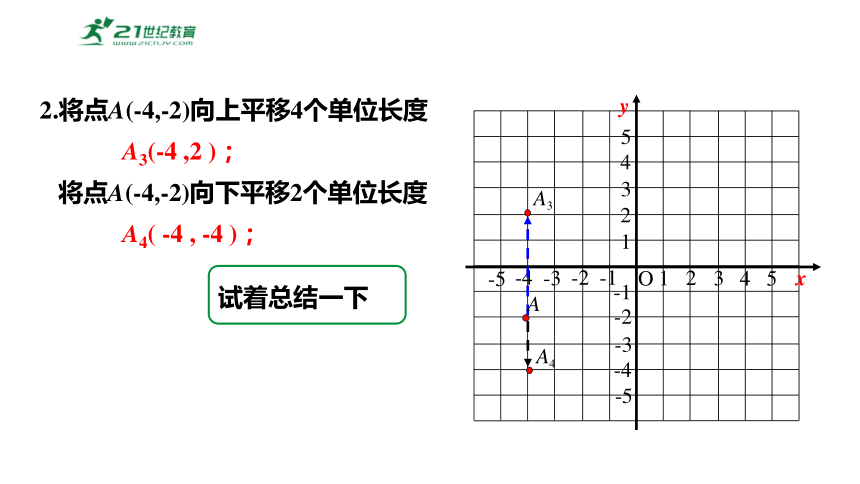
2.将点A(-4,-2)向上平移4个单位长度
A3(-4 ,2 );
将点A(-4,-2)向下平移2个单位长度
A4( -4 , -4 );
试着总结一下
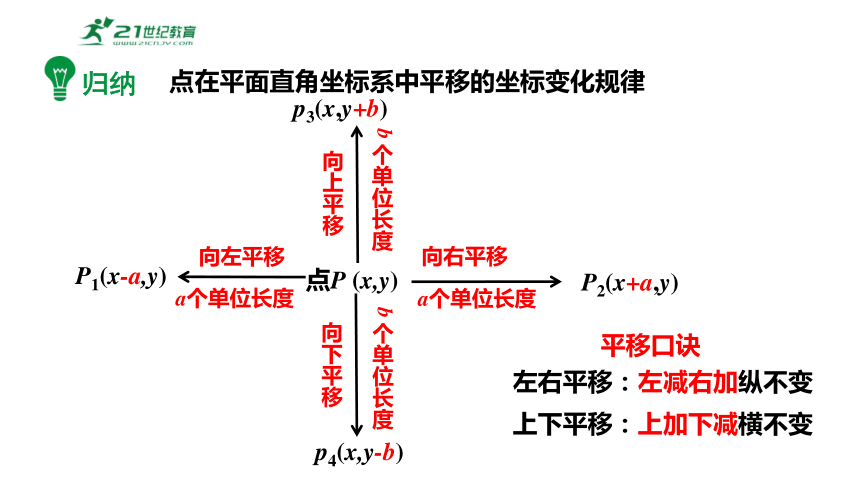
归纳
点在平面直角坐标系中平移的坐标变化规律
平移口诀
左右平移:左减右加纵不变
上下平移:上加下减横不变
点P (x,y)
向左平移
a个单位长度
向右平移
a个单位长度
P1(x-a,y)
P2(x+a,y)
向上平移
b个单位长度
向下平移
b个单位长度
p4(x,y-b)
p3(x,y+b)
(1)点A(3,0)向右平移5个单位长度,得到点A1,A1的坐标为______
(8,0)
(3)点A1(4,5)是由点A(-1,5)经过_____________________得到的.
向右平移5个单位长度
向下平移7个单位长度
(2)点A(3,0)向上平移4个单位长度,得到点A2,A2的坐标为______
(3,4)
(4)点A2(4,-5)是由点A(4,2)经过_____________________得到的.
例1 填空
探究
二 平面直角坐标系中图形的平移
如图,正方形 ABCD 四个顶点的坐标分别是 A (-2, 4),B (-2,3),C (-1,3),D (-1,4),将正方形 ACD 向下平移 7 个单位长度,再向右平移 8 个单位长度,两次平移后四个顶点相应变为点 E,F,G,H,它们的坐标分别是什么?
1
3
5
2
4
6
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
y
x
A
B
C
D
E
F
G
H
E(6,-3),F(6,-4),G(7,-4),H (7,-3).
如果直接平移正方形 ABCD,使点 A 移到点 E,它和我们前面得到的正方形位置相同吗?
1
3
5
2
4
6
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
y
x
A
B
C
D
E
F
G
H
位置相同
归纳
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化.
归纳
图形在平面直角坐标系中的平移变化规律
原坐标 平移方向和平移距离 对应点的坐标
(x,y) 向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , yb)
(xa , y+b)
(xa , yb)
例2 如图,将平行四边形 ABCD 向左平移 2 个单位长度,然后再向上平移 3 个单位长度,可以得到平行四边形 A′B′C′D′,画出平移后的图形,并指出其各个顶点的坐标.
A′
B′
C′
D′
A′(-3,1)
B′(1,1)
C′(2,4)
D′(-2,4)
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化.
反之,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
三 由坐标变化确定平移方式
例3 如图,三角形 ABC 三个顶点的坐标分别是 A (4,3),B (3,1),C (1,2).
(1)将三角形 ABC三个顶点的横坐标都减去 6,纵坐标不变,分别得到点A1,B1,C1,依次连接A1,B1,C1各点,所得三角形A1B1C1与三角形 ABC 的大小、形状和位置有什么关系?
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1(-2,3),B1(-3,1),C1(-5,2);
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
所得三角形 A1B1C1 与三角形 ABC 的大小、形状完全相同,三角形 A1B1C1 可以看作将三角形 ABC向左平移了 6 个单位长度得到.
(2) 将三角形 ABC 三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2,B2,C2,依次连接A2,B2,C2各点,所得三角形A2B2C2与三角形 ABC 的大小、形状和位置有什么关系?
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A2
B2
C2
A2(4,-2),B2(3,-4),C2(1,-3);
所得三角形 A2B2C2与三角形 ABC 的大小、形状完全相同,三角形 A2B2C2 可以看作将三角形 ABC向下平移了 5 个单位长度得到.
思考
(1) 如果将这个问题中的“横坐标都减去 6”变为“横坐标都加 3”,能得出什么结论?画出得到的图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
y
x
A
C
B
A2
B2
C2
A2(7,3),B2(6,1),C2(4,2);
所得三角形 A2B2C2与三角形 ABC 的大小、形状完全相同,三角形 A2B2C2 可以看作将三角形 ABC向右平移了 3 个单位长度得到.
(2) 如果将这个问题中的“纵坐标都减去5”变为“纵坐标都加 2”,能得出什么结论?画出得到的图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A2
B2
C2
A2(4,5),B2(3,3),C2(1,4);
所得三角形 A2B2C2与三角形 ABC 的大小、形状完全相同,三角形 A2B2C2 可以看作将三角形 ABC向上平移了 2 个单位长度得到.
(3) 如果将三角形 ABC 三个顶点的横坐标都减去 6,同时纵坐标都减去 5,能得到什么结论?画出得到的图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
A2
B2
C2
所得三角形A2B2C2可以由三角形 ABC 向左平移 6 个单位长度,再向下平移 5 个单位长度得到.两个三角形的大小、形状完全相同.
归纳
图形上点的坐标变化对应的平移规律
原坐标 对应点的坐标 平移方向和平移距离
(x,y) (x+a , y+b)
(x+a , yb)
(xa , y+b)
(xa , yb)
向右平移 a 个单位长度,向上平移 b 个单位长度
向右平移 a 个单位长度,向下平移 b 个单位长度
向左平移 a 个单位长度,向上平移 b 个单位长度
向左平移 a 个单位长度,向下平移 b 个单位长度
1.已知点A的坐标为(2,1).
(1)将点A向左平移2个单位后得到点B,则点B的坐标为________;
(2)将点A向右平移2个单位后得到点C,则点C的坐标为________;
(3)将点A向上平移2个单位后得到点D,则点D的坐标为________;
(4)将点A向下平移2个单位后得到点E,则点E的坐标为________.
(0,1)
(4,1)
(2,3)
(2,-1)
随堂练习
2.如图,在平面直角坐标系中,已知点A(2,1),B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为( )
A.(-1,-1)
B.(1,0)
C.(-1,0)
D.(3,0)
C
3.将三角形ABC向下平移5个单位会怎样?
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
A
B
C
B1
A1
C1
y
x
解:横坐标不变,各点的纵坐标减去5
A(4,3)→A1(4,-2)
B(3,1)→B1(3,-4)
C(1,2)→C1(1,-3)
4.如图,边长为1的正方形网格内,把△ABC平移到△DEF的位置,
其平移的办法是___________________________________________.
先向右平移5个单位,再向上平移3个单位
A
B
C
D
E
F
用坐标表示
平移
沿y轴平移
纵坐标不变,
横坐标加上一个正数,则向右平移;
横坐标减去一个正数,向左平移.
沿x轴平移
横坐标不变,
纵坐标加上一个正数,向上平移;
纵坐标减去一个正数,向下平移
课堂小结
七年级下
人教版
7.2.2 用坐标表示平移
1.在平面直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移一定距离后图形的顶点坐标,知道对应顶点坐标之间的关系.
2.在平面直角坐标系中,探索并了解将一个多边形依次沿两个坐标轴方向平移后所得到的图形和原来图形具有平移关系,体会图形顶点坐标的变化.
学习目标
重点
难点
1. 什么叫平移?
3 .平移后得到的新图形与原图形有什么关系?
在平面内,把一个图形整体沿某一方向移动一定的距离,这种图形的变换叫做平移.
2.平移的要素是什么?
平移的方向、平移的距离
①平移只改变图形的位置,形状和大小不变.
②对应点的连线互相平行(或在同一条直线上)且相等.
新课引入
探究
1.将点A(-2,2)向右平移5个单位长度
如图,请写出平移后的点的坐标.
1
3
5
2
4
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-5
1
A1
A2
y
x
A
A1(3,2);
将点A(-2,2)向左平移2个单位长度
A2(-4,2);
你发现了什么?
新知学面直角坐标系中点的平移
1
3
5
2
4
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-5
1
A4
y
x
A
A3
2.将点A(-4,-2)向上平移4个单位长度
A3(-4 ,2 );
将点A(-4,-2)向下平移2个单位长度
A4( -4 , -4 );
试着总结一下
归纳
点在平面直角坐标系中平移的坐标变化规律
平移口诀
左右平移:左减右加纵不变
上下平移:上加下减横不变
点P (x,y)
向左平移
a个单位长度
向右平移
a个单位长度
P1(x-a,y)
P2(x+a,y)
向上平移
b个单位长度
向下平移
b个单位长度
p4(x,y-b)
p3(x,y+b)
(1)点A(3,0)向右平移5个单位长度,得到点A1,A1的坐标为______
(8,0)
(3)点A1(4,5)是由点A(-1,5)经过_____________________得到的.
向右平移5个单位长度
向下平移7个单位长度
(2)点A(3,0)向上平移4个单位长度,得到点A2,A2的坐标为______
(3,4)
(4)点A2(4,-5)是由点A(4,2)经过_____________________得到的.
例1 填空
探究
二 平面直角坐标系中图形的平移
如图,正方形 ABCD 四个顶点的坐标分别是 A (-2, 4),B (-2,3),C (-1,3),D (-1,4),将正方形 ACD 向下平移 7 个单位长度,再向右平移 8 个单位长度,两次平移后四个顶点相应变为点 E,F,G,H,它们的坐标分别是什么?
1
3
5
2
4
6
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
y
x
A
B
C
D
E
F
G
H
E(6,-3),F(6,-4),G(7,-4),H (7,-3).
如果直接平移正方形 ABCD,使点 A 移到点 E,它和我们前面得到的正方形位置相同吗?
1
3
5
2
4
6
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
y
x
A
B
C
D
E
F
G
H
位置相同
归纳
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化.
归纳
图形在平面直角坐标系中的平移变化规律
原坐标 平移方向和平移距离 对应点的坐标
(x,y) 向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , yb)
(xa , y+b)
(xa , yb)
例2 如图,将平行四边形 ABCD 向左平移 2 个单位长度,然后再向上平移 3 个单位长度,可以得到平行四边形 A′B′C′D′,画出平移后的图形,并指出其各个顶点的坐标.
A′
B′
C′
D′
A′(-3,1)
B′(1,1)
C′(2,4)
D′(-2,4)
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化.
反之,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
三 由坐标变化确定平移方式
例3 如图,三角形 ABC 三个顶点的坐标分别是 A (4,3),B (3,1),C (1,2).
(1)将三角形 ABC三个顶点的横坐标都减去 6,纵坐标不变,分别得到点A1,B1,C1,依次连接A1,B1,C1各点,所得三角形A1B1C1与三角形 ABC 的大小、形状和位置有什么关系?
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1(-2,3),B1(-3,1),C1(-5,2);
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
所得三角形 A1B1C1 与三角形 ABC 的大小、形状完全相同,三角形 A1B1C1 可以看作将三角形 ABC向左平移了 6 个单位长度得到.
(2) 将三角形 ABC 三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2,B2,C2,依次连接A2,B2,C2各点,所得三角形A2B2C2与三角形 ABC 的大小、形状和位置有什么关系?
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A2
B2
C2
A2(4,-2),B2(3,-4),C2(1,-3);
所得三角形 A2B2C2与三角形 ABC 的大小、形状完全相同,三角形 A2B2C2 可以看作将三角形 ABC向下平移了 5 个单位长度得到.
思考
(1) 如果将这个问题中的“横坐标都减去 6”变为“横坐标都加 3”,能得出什么结论?画出得到的图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
y
x
A
C
B
A2
B2
C2
A2(7,3),B2(6,1),C2(4,2);
所得三角形 A2B2C2与三角形 ABC 的大小、形状完全相同,三角形 A2B2C2 可以看作将三角形 ABC向右平移了 3 个单位长度得到.
(2) 如果将这个问题中的“纵坐标都减去5”变为“纵坐标都加 2”,能得出什么结论?画出得到的图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A2
B2
C2
A2(4,5),B2(3,3),C2(1,4);
所得三角形 A2B2C2与三角形 ABC 的大小、形状完全相同,三角形 A2B2C2 可以看作将三角形 ABC向上平移了 2 个单位长度得到.
(3) 如果将三角形 ABC 三个顶点的横坐标都减去 6,同时纵坐标都减去 5,能得到什么结论?画出得到的图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
A2
B2
C2
所得三角形A2B2C2可以由三角形 ABC 向左平移 6 个单位长度,再向下平移 5 个单位长度得到.两个三角形的大小、形状完全相同.
归纳
图形上点的坐标变化对应的平移规律
原坐标 对应点的坐标 平移方向和平移距离
(x,y) (x+a , y+b)
(x+a , yb)
(xa , y+b)
(xa , yb)
向右平移 a 个单位长度,向上平移 b 个单位长度
向右平移 a 个单位长度,向下平移 b 个单位长度
向左平移 a 个单位长度,向上平移 b 个单位长度
向左平移 a 个单位长度,向下平移 b 个单位长度
1.已知点A的坐标为(2,1).
(1)将点A向左平移2个单位后得到点B,则点B的坐标为________;
(2)将点A向右平移2个单位后得到点C,则点C的坐标为________;
(3)将点A向上平移2个单位后得到点D,则点D的坐标为________;
(4)将点A向下平移2个单位后得到点E,则点E的坐标为________.
(0,1)
(4,1)
(2,3)
(2,-1)
随堂练习
2.如图,在平面直角坐标系中,已知点A(2,1),B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为( )
A.(-1,-1)
B.(1,0)
C.(-1,0)
D.(3,0)
C
3.将三角形ABC向下平移5个单位会怎样?
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
A
B
C
B1
A1
C1
y
x
解:横坐标不变,各点的纵坐标减去5
A(4,3)→A1(4,-2)
B(3,1)→B1(3,-4)
C(1,2)→C1(1,-3)
4.如图,边长为1的正方形网格内,把△ABC平移到△DEF的位置,
其平移的办法是___________________________________________.
先向右平移5个单位,再向上平移3个单位
A
B
C
D
E
F
用坐标表示
平移
沿y轴平移
纵坐标不变,
横坐标加上一个正数,则向右平移;
横坐标减去一个正数,向左平移.
沿x轴平移
横坐标不变,
纵坐标加上一个正数,向上平移;
纵坐标减去一个正数,向下平移
课堂小结
