9.1.1不等式及其解集 课件(共24张PPT)
文档属性
| 名称 | 9.1.1不等式及其解集 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:35:11 | ||
图片预览








文档简介
(共24张PPT)
9.1.1 不等式及其解集
七年级下
人教版
1. 结合具体问题,了解不等式的意义;
2. 能根据具体问题中的数量关系,列出不等式.
学习目标
重点
难点
某公交公司推出公交卡充值优惠活动,若充值100元,则不享受优惠;若充值超过100元但不超过200元,享受9折优惠.设小明一次充值了a元,若小明想享受9折优惠,你能用数学语言表示出a的取值范围吗?
新课引入
100新知学习
问题
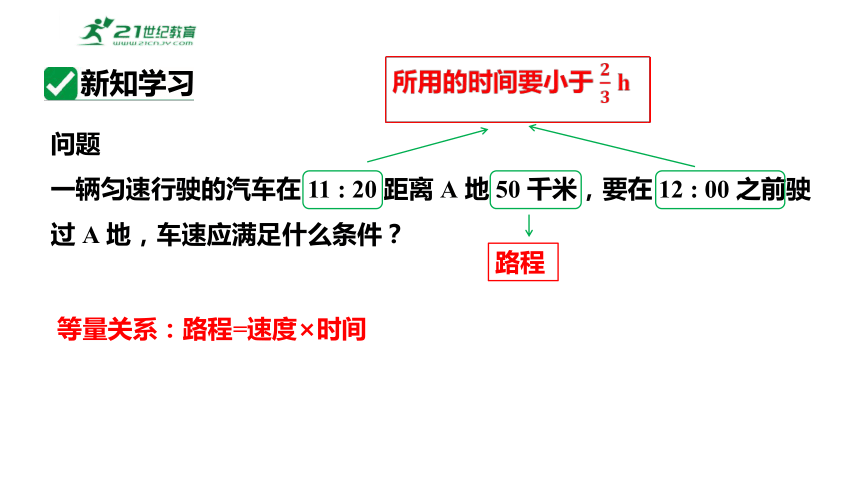
一辆匀速行驶的汽车在 11 : 20 距离 A 地 50 千米,要在 12 : 00 之前驶过 A 地,车速应满足什么条件?
所用的时间要小于 h
路程
等量关系:路程=速度×时间
新知学习
问题 一辆匀速行驶的汽车在 11 : 20 距离 A 地 50 千米,要在 12 : 00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从时间上看,汽车要在 12 : 00 之前驶过 A 地,
则以这个速度行驶 50 km 所用的时间不到 h,即
. ①
从路程上看,汽车要在 12 : 00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即
. ②
式子①和②从不同角度表示了车速应满足的条件.
归纳
像①和②这样用符号“<”或“>”表示大小关系的式子,叫做不等式.
思考1
,这两个式子和之前学的方程有什么相同点和不同?
相同点:都含有未知数;
不同点:方程是用等号连接式子两边,这两个式子是用不等号连接式子两边.
注意
1.有些不等式中不含未知数,例如3<4,-1>-2.
2.有些不等式中含有未知数,例如2x>3中字母x表示未知数.
3.像a+2≠a-2这样用“≠”表示不等关系的式子也是不等式.
例1 下列是不等式的是________________
①2x>3; ②-3a<5; ③5x=13; ④b≥3; ⑤-y≤7;
⑥3<4; ⑦a+2≠a-2;
①②④⑤⑥⑦
常见的表示不等关系的符号有“<”“>”“≤”“≥”“≠”.
例2 用不等式表示:
(1)a是非负数.
(2)直角三角形斜边c比它的两直角边 a,b都长;
(3)x与17的和比它的5倍小.
a ≥ 0
c>a且c>b
x+17<5x
思考2
在问题中,我们从题干中的一些关键词得到大小关系,还有哪些词语,也具有这样的作用呢?
(4)两数x、y的平方和不小于这两数积的2倍.
(5)2x 与 3 的和不大于-6;
(6)三角形的一条边a的长度不等于另一条边b的长度.
(7)某商店今天的收入a少于支出b.
x2+y2 ≥ 2xy
2x + 3 ≤ – 6
a≠b
a符号 读法 不等关系词
< 小于 小于、不足、少于
> 大于 大于、超出
≤ 小于或等于 不大于、不超过、至多、最多
≥ 大于或等于 不小于、不低于、至少、最少
≠ 不等于 不相等
常见的表示不等关系的词语
还记得我们刚开始学习求一元一次方程的解时所用的方法吗
猜测法+
试验法
方程 1700 + 150x = 2450 中未知数 x 的值是多少?
分析:当 x = 1 时,1700 + 150x = 1700 + 150×1 = 1850;
当 x = 2 时,1700 + 150x = 1700 + 150×2 = 2000;
当 x = 3 时,1700 + 150x = 1700 + 150×3 = 2150;
x 1 2 3 4 5 …
1700+150x 1850 2000 2150
当 x = 4 时,1700 + 150x = 1700 + 150×4 = 2300.
当 x = 5 时, 1700 + 150x = 1700 + 150×5 = 2450,
这时方程 1700 + 150x = 2450 等号左右两边相等.
2450
x = 5 叫做方程 1700 + 150x = 2450 的解.
这就是说,方程 1700 + 150x = 2450 中未知数x的值应是 5.
2300
思考3
下面给出的数,能使不等式 成立吗?
如何求出的解呢
x 73 74 75 76 77 78
不成立
不成立
成立
成立
不成立
成立
50
52
若成立,说明什么?
说明这个数是不等式的解.
归纳
能使不等式成立的未知数的值叫做不等式的解.
思考4
除了76,77和78,不等式还有其他解吗?
x 73 74 75 76 77 78
不成立
不成立
成立
成立
不成立
成立
50
52
可以发现,当 时,不等式 总成立;而当x<75或x=75时,不等式 不成立.
这就是说,任何一个大于75的数都是不等式>50的解,这样的解有无数个;任何一个小于或等于75的数都不是不等式>50的解.因此,x>75表示了能使不等式>50成立的x的取值范围,它可以在数轴上表示如下图.
0 75
画空心圆圈,表示不包含这一点.
由上可知,汽车要在12:00之前驶过A地,车速必须大于75km/h.
归纳
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
求不等式的解集的过程叫做解不等式.
例3 下列数中哪些是不等式x+3>6的解?哪些不是?
-4,-2.5,0,1,2.5,3,3.2,4.8,8,12
x -4 -2.5 0 1 2.5 3 3.2 4.8 8 12
x+3
x+3>6
否
是
-1
11
4
5.5
6
6.2
7.8
15
0.5
3
否
否
否
否
否
是
是
是
由上表可知,3.2,4.8,8,12是不等式x+3>6的解,其余数不是.
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别
联系 解集包含所有的解,所有的解组成解集.
能使不等式成立的未知数的值.
能使不等式成立的所有未知数的值.
归纳
随堂练习
1.下面给出了5个式子:①3>0;②4+3y>0;③x=3;④x-1;
⑤x+2≤3;⑥2x≠0,其中不等式有( )
C
A、2个 B、3个 C、4个 D、5个
2.下列各数中,是不等式3x-2>1的解的是 ( )
A.1 B.2 C.0 D.-1
B
3.用不等式表示:
(1)奶奶在水果摊上称了3斤苹果,摊主称了几个苹果说:“你看秤,高高的.”如果设苹果的实际质量为x斤,则“高高的”的意思用不等式表示出来是_______________
x≥3
(2) x+3与y-5的平方和一定是非负数,用不等式表示为_________________________.
(x+3)2+(y-5)2≥0
(3)大气层又称大气圈,是地球最外部的气体圈层,没有确切的界限,但可以估计其厚度在1 000 km以上.设大气层厚度为x km,则用不等式表示为_________.
x>1000
4.直接说出下列不等式的解集:
(1) x+3>6 (2) 2x<8 (3) x-2>0
解:(1) x>3
(2) x<4
(3) x>2
解集
不等式概念
不等式及其
解集
解
用符号“<”或“>”表示大小关系的式子,叫做不等式.
使不等式成立的未知数的值
课堂小结
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集
9.1.1 不等式及其解集
七年级下
人教版
1. 结合具体问题,了解不等式的意义;
2. 能根据具体问题中的数量关系,列出不等式.
学习目标
重点
难点
某公交公司推出公交卡充值优惠活动,若充值100元,则不享受优惠;若充值超过100元但不超过200元,享受9折优惠.设小明一次充值了a元,若小明想享受9折优惠,你能用数学语言表示出a的取值范围吗?
新课引入
100
问题
一辆匀速行驶的汽车在 11 : 20 距离 A 地 50 千米,要在 12 : 00 之前驶过 A 地,车速应满足什么条件?
所用的时间要小于 h
路程
等量关系:路程=速度×时间
新知学习
问题 一辆匀速行驶的汽车在 11 : 20 距离 A 地 50 千米,要在 12 : 00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从时间上看,汽车要在 12 : 00 之前驶过 A 地,
则以这个速度行驶 50 km 所用的时间不到 h,即
. ①
从路程上看,汽车要在 12 : 00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即
. ②
式子①和②从不同角度表示了车速应满足的条件.
归纳
像①和②这样用符号“<”或“>”表示大小关系的式子,叫做不等式.
思考1
,这两个式子和之前学的方程有什么相同点和不同?
相同点:都含有未知数;
不同点:方程是用等号连接式子两边,这两个式子是用不等号连接式子两边.
注意
1.有些不等式中不含未知数,例如3<4,-1>-2.
2.有些不等式中含有未知数,例如2x>3中字母x表示未知数.
3.像a+2≠a-2这样用“≠”表示不等关系的式子也是不等式.
例1 下列是不等式的是________________
①2x>3; ②-3a<5; ③5x=13; ④b≥3; ⑤-y≤7;
⑥3<4; ⑦a+2≠a-2;
①②④⑤⑥⑦
常见的表示不等关系的符号有“<”“>”“≤”“≥”“≠”.
例2 用不等式表示:
(1)a是非负数.
(2)直角三角形斜边c比它的两直角边 a,b都长;
(3)x与17的和比它的5倍小.
a ≥ 0
c>a且c>b
x+17<5x
思考2
在问题中,我们从题干中的一些关键词得到大小关系,还有哪些词语,也具有这样的作用呢?
(4)两数x、y的平方和不小于这两数积的2倍.
(5)2x 与 3 的和不大于-6;
(6)三角形的一条边a的长度不等于另一条边b的长度.
(7)某商店今天的收入a少于支出b.
x2+y2 ≥ 2xy
2x + 3 ≤ – 6
a≠b
a
< 小于 小于、不足、少于
> 大于 大于、超出
≤ 小于或等于 不大于、不超过、至多、最多
≥ 大于或等于 不小于、不低于、至少、最少
≠ 不等于 不相等
常见的表示不等关系的词语
还记得我们刚开始学习求一元一次方程的解时所用的方法吗
猜测法+
试验法
方程 1700 + 150x = 2450 中未知数 x 的值是多少?
分析:当 x = 1 时,1700 + 150x = 1700 + 150×1 = 1850;
当 x = 2 时,1700 + 150x = 1700 + 150×2 = 2000;
当 x = 3 时,1700 + 150x = 1700 + 150×3 = 2150;
x 1 2 3 4 5 …
1700+150x 1850 2000 2150
当 x = 4 时,1700 + 150x = 1700 + 150×4 = 2300.
当 x = 5 时, 1700 + 150x = 1700 + 150×5 = 2450,
这时方程 1700 + 150x = 2450 等号左右两边相等.
2450
x = 5 叫做方程 1700 + 150x = 2450 的解.
这就是说,方程 1700 + 150x = 2450 中未知数x的值应是 5.
2300
思考3
下面给出的数,能使不等式 成立吗?
如何求出的解呢
x 73 74 75 76 77 78
不成立
不成立
成立
成立
不成立
成立
50
52
若成立,说明什么?
说明这个数是不等式的解.
归纳
能使不等式成立的未知数的值叫做不等式的解.
思考4
除了76,77和78,不等式还有其他解吗?
x 73 74 75 76 77 78
不成立
不成立
成立
成立
不成立
成立
50
52
可以发现,当 时,不等式 总成立;而当x<75或x=75时,不等式 不成立.
这就是说,任何一个大于75的数都是不等式>50的解,这样的解有无数个;任何一个小于或等于75的数都不是不等式>50的解.因此,x>75表示了能使不等式>50成立的x的取值范围,它可以在数轴上表示如下图.
0 75
画空心圆圈,表示不包含这一点.
由上可知,汽车要在12:00之前驶过A地,车速必须大于75km/h.
归纳
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
求不等式的解集的过程叫做解不等式.
例3 下列数中哪些是不等式x+3>6的解?哪些不是?
-4,-2.5,0,1,2.5,3,3.2,4.8,8,12
x -4 -2.5 0 1 2.5 3 3.2 4.8 8 12
x+3
x+3>6
否
是
-1
11
4
5.5
6
6.2
7.8
15
0.5
3
否
否
否
否
否
是
是
是
由上表可知,3.2,4.8,8,12是不等式x+3>6的解,其余数不是.
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别
联系 解集包含所有的解,所有的解组成解集.
能使不等式成立的未知数的值.
能使不等式成立的所有未知数的值.
归纳
随堂练习
1.下面给出了5个式子:①3>0;②4+3y>0;③x=3;④x-1;
⑤x+2≤3;⑥2x≠0,其中不等式有( )
C
A、2个 B、3个 C、4个 D、5个
2.下列各数中,是不等式3x-2>1的解的是 ( )
A.1 B.2 C.0 D.-1
B
3.用不等式表示:
(1)奶奶在水果摊上称了3斤苹果,摊主称了几个苹果说:“你看秤,高高的.”如果设苹果的实际质量为x斤,则“高高的”的意思用不等式表示出来是_______________
x≥3
(2) x+3与y-5的平方和一定是非负数,用不等式表示为_________________________.
(x+3)2+(y-5)2≥0
(3)大气层又称大气圈,是地球最外部的气体圈层,没有确切的界限,但可以估计其厚度在1 000 km以上.设大气层厚度为x km,则用不等式表示为_________.
x>1000
4.直接说出下列不等式的解集:
(1) x+3>6 (2) 2x<8 (3) x-2>0
解:(1) x>3
(2) x<4
(3) x>2
解集
不等式概念
不等式及其
解集
解
用符号“<”或“>”表示大小关系的式子,叫做不等式.
使不等式成立的未知数的值
课堂小结
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集
