9.3 一元一次不等式组课件(共25张PPT)
文档属性
| 名称 | 9.3 一元一次不等式组课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:35:11 | ||
图片预览







文档简介
(共25张PPT)
9.3 一元一次不等式组
七年级下
人教版
2.会用数轴确定两个一元一次不等式组成的不等式组的解集.
1.了解一元一次不等式组的相关概念.
学习目标
重点
重点
难点
你会用不等式表示下面的实际问题吗?
1.某地某一天最低气温3℃,最高气温25℃,则当天的温度t(℃)的范围为__________
2.三角形一条边长为3,另一条边长为6,则第三条边长 l 的取值范围为__________
t≥3且t≤25
l>3且l<9
新课引入
新知学习
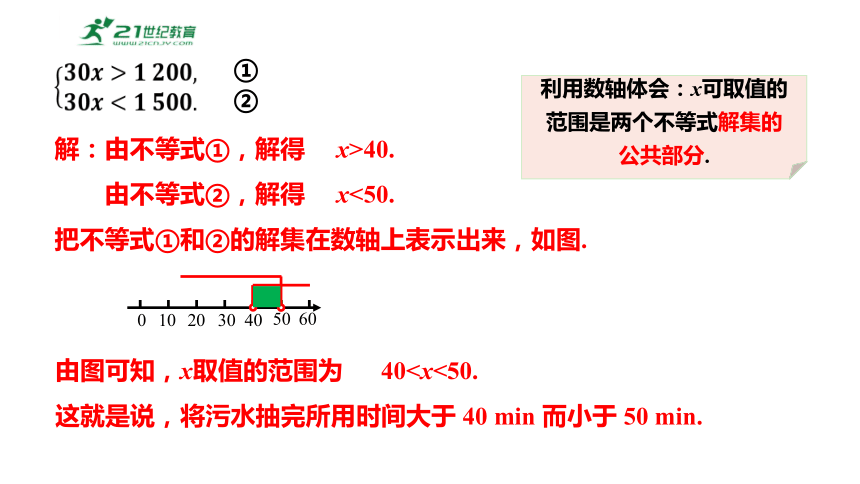
问题 用每分可抽 30 t 水的抽水机来抽污水管道里积存的污水,估计积存的污水超过 1 200 t 而不足 1 500 t,那么将污水抽完所用时间的范围是什么?
设用 x min 将污水抽完,则 x 同时满足不等式:
30x>1 200 ①
30x<1 500 ②
类似于方程组,把几个含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组,记作
注意:一元一次不等式组必须同时满足三个条件:
①每个不等式都是一元一次不等式;
②含有同一个未知数;
③不等式的个数不少于2.
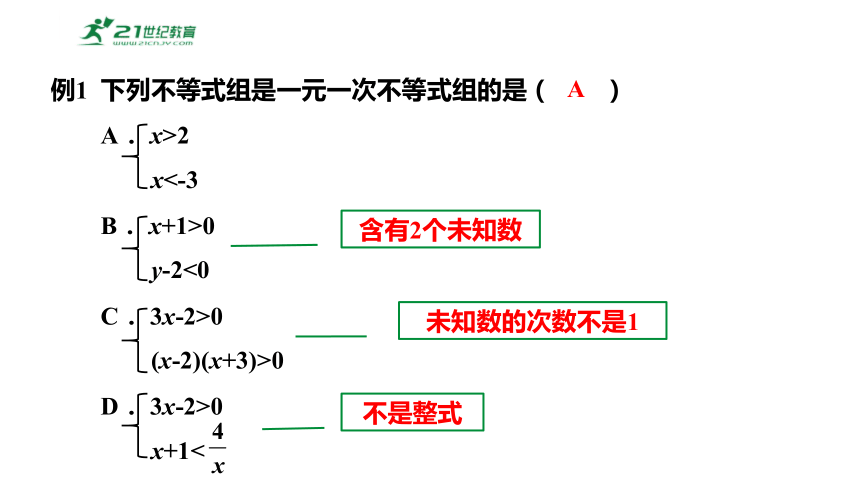
例1 下列不等式组是一元一次不等式组的是( )
A. x>2
x<-3
B. x+1>0
y-2<0
C. 3x-2>0
(x-2)(x+3)>0
D. 3x-2>0
x+1<
A
含有2个未知数
未知数的次数不是1
不是整式
怎样确定下面不等式组中x的可取值的范围呢?
分析:类比方程组的解,不等式组中的各不等式解集的公共部分,就是不等式组中x可以取值的范围.
探究
解:由不等式①,解得 x>40.
由不等式②,解得 x<50.
把不等式①和②的解集在数轴上表示出来,如图.
由图可知,x取值的范围为 40这就是说,将污水抽完所用时间大于 40 min 而小于 50 min.
①
②
50
30
0
10
20
40
60
利用数轴体会:x可取值的
范围是两个不等式解集的
公共部分.
归纳
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.解不等式组就是求它的解集.
例2 解下列不等式组
2x-1>x+1 ①
x+8<4x-1 ②
解:(1)解不等式①,得 x>2
解不等式②,得 x>3
把不等式①和②的解集在数轴上表示出来,如图.
0
2
3
从图可以找出两个不等式解集的公共部分,得不等式组的解集x>3.
(1)
利用数轴可以确定不等式组的解集.
(2)
解:(2)解不等式①,得 x≥8.
解不等式②,得 x<.
把不等式①和②的解集在数轴上表示出来,如图.
8
0
从图可以看到这两个不等式的解集没有公共部分,不等式组无解.
归纳
“同大取大”
“同小取小”
“大小、小大中间找”
“大大、小小无解”
一元一次不等式组的解集分类 (前提条件:a不等式组的解集为 : a不等式组的解集为 : x不等式组的解集为 : x>b
不等式组无解
确定一元一次不等式组的解集的两种方法
(1)数轴法:把不等式组中每个不等式的解集在数轴上表示出来,找出这些解集的公共部分,就得到不等式组的解集;若无公共部分,则不等式组无解.
(2)口诀法:同大取大,同小取小,大小小大中间找,大大小小无解.
归纳
例3 x 取哪些整数值时,不等式 5x+2>3(x-1) 与 都成立?
分析:求出这两个不等式组成的不等式组的解集,解集中的整数就是x
可取的整数值.
解:解不等式组
得 -所以 x 可取的整数值是 -2,-1,0,1,2,3,4.
1.如图,解集是数轴上表示的不等式组为( )
A. x-2≥0, B. x+2≥0,
3-x>0 x-3>0
C. x-2≥0, D. 2-x≥0,
3+x>0 3-x>0
A
随堂练习
2. 在平面直角坐标系中,点P(6-2x,x-5)在第三象限,则x的取值范围是( )
A. x>5 B. 3<x<5
C. x<3 D. -3<x<5
B
把不等式①和②的解集在数轴上表示出来,如图:
因此,原不等式组的解集为解:解不等式①,得 解不等式②,得
-3 -2 -1 0 1 2 3 4 5 6 7 8
3.解下列不等式组:
x-1<3 ①
x+1<3 ②
解:解不等式①,得x<4 解不等式②,得x<2
把不等式①和②的解集在数轴上表示出来,如图:
因此,原不等式组的解集为x<2
0
2
3
4
1
(2)
2x+3<7 ①
5x-6>9 ②
解:解不等式①,得x<2 解不等式②,得x>3
在同一条数轴上表示不等式①②的解集,如图:
因此,原不等式组无解.
0
2
3
1
(3)
4.解不等式组: 2-x<x≤6-2x,并求出它的整数解.
解:解不等式组
2-x<x
得:1<x≤2,
x 可取的整数值是:2.
x≤6-2x
5. 把一些书分给几名同学,如果每人分 3 本,那么余 8 本;如果前面的每名同学分 5 本,那么最后一人就分不到 3 本,这些书有多少本?共有多少人?
解:设共有 x 人,根据题意,得
解得5<x≤6.5.
由x应为正整数,得 x=6.
3x+8=3×6+8=26.
答:这些书有 26 本,共有 6 人.
3x+8-5(x-1)≥0
3x+8-5(x-1)<3
6.某商店购进A、B两种商品,购买1个A商品需要15元,购买一个B商品需要5元.商店准备购买A、B两种商品共80个,若A商品的数量不少于B商品数量的4倍,并且购买A、B商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
解:设购买B商品x个,则购买A商品(80-x)个,依题意,
得: , 解得:
由x应为正整数,
所以x=15或16
所以商店有2种购买方案,
方案①:购进A商品65个、B商品15个;
方案②:购进A商品64个、B商品16个.
解集确定
方法
概念
一元一次
不等式组
解集
把几个含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集
课堂小结
①数轴法
②口诀法
一元一次不等式组的解集分类口诀:
前提条件:ax>a
x>b
同大取大
解集:x>b
xx解集:x同小取小
大小、小大中间找
大大、小小无解
x>a
x解集:axx>b
解集:无解
9.3 一元一次不等式组
七年级下
人教版
2.会用数轴确定两个一元一次不等式组成的不等式组的解集.
1.了解一元一次不等式组的相关概念.
学习目标
重点
重点
难点
你会用不等式表示下面的实际问题吗?
1.某地某一天最低气温3℃,最高气温25℃,则当天的温度t(℃)的范围为__________
2.三角形一条边长为3,另一条边长为6,则第三条边长 l 的取值范围为__________
t≥3且t≤25
l>3且l<9
新课引入
新知学习
问题 用每分可抽 30 t 水的抽水机来抽污水管道里积存的污水,估计积存的污水超过 1 200 t 而不足 1 500 t,那么将污水抽完所用时间的范围是什么?
设用 x min 将污水抽完,则 x 同时满足不等式:
30x>1 200 ①
30x<1 500 ②
类似于方程组,把几个含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组,记作
注意:一元一次不等式组必须同时满足三个条件:
①每个不等式都是一元一次不等式;
②含有同一个未知数;
③不等式的个数不少于2.
例1 下列不等式组是一元一次不等式组的是( )
A. x>2
x<-3
B. x+1>0
y-2<0
C. 3x-2>0
(x-2)(x+3)>0
D. 3x-2>0
x+1<
A
含有2个未知数
未知数的次数不是1
不是整式
怎样确定下面不等式组中x的可取值的范围呢?
分析:类比方程组的解,不等式组中的各不等式解集的公共部分,就是不等式组中x可以取值的范围.
探究
解:由不等式①,解得 x>40.
由不等式②,解得 x<50.
把不等式①和②的解集在数轴上表示出来,如图.
由图可知,x取值的范围为 40
①
②
50
30
0
10
20
40
60
利用数轴体会:x可取值的
范围是两个不等式解集的
公共部分.
归纳
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.解不等式组就是求它的解集.
例2 解下列不等式组
2x-1>x+1 ①
x+8<4x-1 ②
解:(1)解不等式①,得 x>2
解不等式②,得 x>3
把不等式①和②的解集在数轴上表示出来,如图.
0
2
3
从图可以找出两个不等式解集的公共部分,得不等式组的解集x>3.
(1)
利用数轴可以确定不等式组的解集.
(2)
解:(2)解不等式①,得 x≥8.
解不等式②,得 x<.
把不等式①和②的解集在数轴上表示出来,如图.
8
0
从图可以看到这两个不等式的解集没有公共部分,不等式组无解.
归纳
“同大取大”
“同小取小”
“大小、小大中间找”
“大大、小小无解”
一元一次不等式组的解集分类 (前提条件:a
不等式组无解
确定一元一次不等式组的解集的两种方法
(1)数轴法:把不等式组中每个不等式的解集在数轴上表示出来,找出这些解集的公共部分,就得到不等式组的解集;若无公共部分,则不等式组无解.
(2)口诀法:同大取大,同小取小,大小小大中间找,大大小小无解.
归纳
例3 x 取哪些整数值时,不等式 5x+2>3(x-1) 与 都成立?
分析:求出这两个不等式组成的不等式组的解集,解集中的整数就是x
可取的整数值.
解:解不等式组
得 -
1.如图,解集是数轴上表示的不等式组为( )
A. x-2≥0, B. x+2≥0,
3-x>0 x-3>0
C. x-2≥0, D. 2-x≥0,
3+x>0 3-x>0
A
随堂练习
2. 在平面直角坐标系中,点P(6-2x,x-5)在第三象限,则x的取值范围是( )
A. x>5 B. 3<x<5
C. x<3 D. -3<x<5
B
把不等式①和②的解集在数轴上表示出来,如图:
因此,原不等式组的解集为
-3 -2 -1 0 1 2 3 4 5 6 7 8
3.解下列不等式组:
x-1<3 ①
x+1<3 ②
解:解不等式①,得x<4 解不等式②,得x<2
把不等式①和②的解集在数轴上表示出来,如图:
因此,原不等式组的解集为x<2
0
2
3
4
1
(2)
2x+3<7 ①
5x-6>9 ②
解:解不等式①,得x<2 解不等式②,得x>3
在同一条数轴上表示不等式①②的解集,如图:
因此,原不等式组无解.
0
2
3
1
(3)
4.解不等式组: 2-x<x≤6-2x,并求出它的整数解.
解:解不等式组
2-x<x
得:1<x≤2,
x 可取的整数值是:2.
x≤6-2x
5. 把一些书分给几名同学,如果每人分 3 本,那么余 8 本;如果前面的每名同学分 5 本,那么最后一人就分不到 3 本,这些书有多少本?共有多少人?
解:设共有 x 人,根据题意,得
解得5<x≤6.5.
由x应为正整数,得 x=6.
3x+8=3×6+8=26.
答:这些书有 26 本,共有 6 人.
3x+8-5(x-1)≥0
3x+8-5(x-1)<3
6.某商店购进A、B两种商品,购买1个A商品需要15元,购买一个B商品需要5元.商店准备购买A、B两种商品共80个,若A商品的数量不少于B商品数量的4倍,并且购买A、B商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
解:设购买B商品x个,则购买A商品(80-x)个,依题意,
得: , 解得:
由x应为正整数,
所以x=15或16
所以商店有2种购买方案,
方案①:购进A商品65个、B商品15个;
方案②:购进A商品64个、B商品16个.
解集确定
方法
概念
一元一次
不等式组
解集
把几个含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集
课堂小结
①数轴法
②口诀法
一元一次不等式组的解集分类口诀:
前提条件:a
x>b
同大取大
解集:x>b
x
大小、小大中间找
大大、小小无解
x>a
x
解集:无解
