3.2用关系式表示的变量间关系 课件(共23张PPT)
文档属性
| 名称 | 3.2用关系式表示的变量间关系 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:35:11 | ||
图片预览






文档简介
(共23张PPT)
3.2 用关系式表示的变量间关系
七年级下
北师版
1.能根据具体情景,用关系式表示变量间的关系,并会根据关系式求值,初步体会自变量和因变量的数值对应关系.
2.能将具体问题抽象成数学问题并将它用关系式表示出来.
难点
重点
学习目标
在上节课的“小车下滑的时间”实验中,
新课引入
①支撑物的高度h和小车下滑的时间 t 都在变化,它们都是______.
变量
②其中小车下滑的时间 t 随支撑物的高度 h 的变化而______.
变化
③支撑物的高度 h 是_______,小车下滑的时间t 是________.
自变量
因变量
数青蛙:
一只青蛙一张嘴,两只眼睛四条腿;两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿;……
1. 青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2. 青蛙的腿数和只数有关系吗?能用数学式表达吗?
有,假设青蛙有a只,则青蛙的眼睛数有y只,则数学表达式为y=2a只.
有,假设青蛙有a只,则青蛙的腿数有b只,则数学表达式为b=4a只.
y=2a和b=4a就是用数学表达式表示的变量之间的关系,也是我们本节课要学习的主要内容.
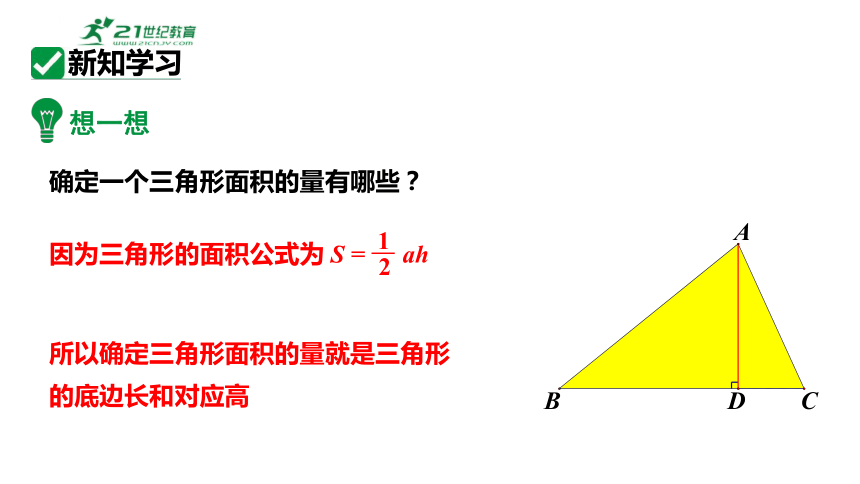
确定一个三角形面积的量有哪些?
D
B
C
A
所以确定三角形面积的量就是三角形
的底边长和对应高
新知学习
S = ah
1
2
因为三角形的面积公式为
想一想
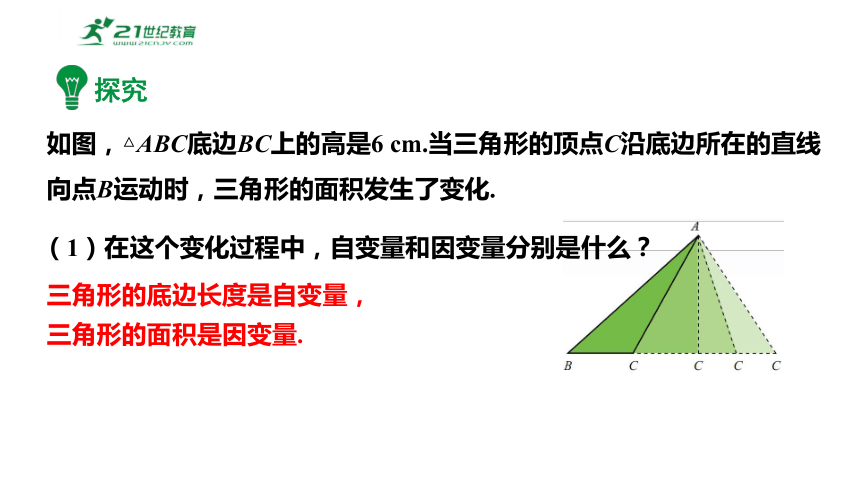
如图,△ABC底边BC上的高是6 cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量和因变量分别是什么?
三角形的底边长度是自变量,
三角形的面积是因变量.
探究
(2)如果三角形的底边长为 x(厘米),那么三角形的面积 y(cm2)可以表示为________.
y=3x
(3)当底边长从12厘米变化到3厘米时,三角形的面积从_____cm2变化到_____cm2.
36
9
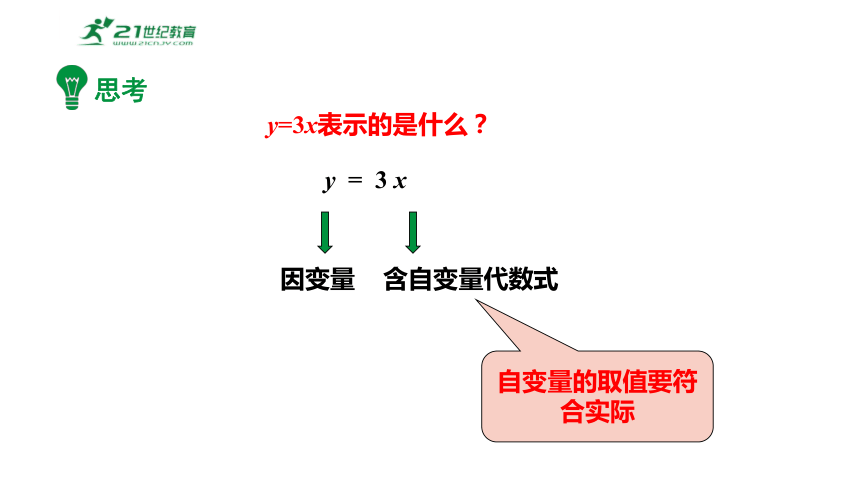
y=3x表示的是什么?
y = 3 x
因变量
含自变量代数式
自变量的取值要符合实际
思考
用来表示自变量和因变量之间关系的等式叫做关系式,利用关系式,如y=3x,我们可以根据任何一个自变量值求出相应的因变量的值.
注意:关系式是一个等式;通常把因变量写在等号的左边,含有自变量的代数式写在等号的右边.
归纳
1.关系式的基本特征是:
①等式的左边是因变量,等式的右边是关于自变量的代数式
②等式中只含有自变量和因变量这两个变量,其他的量都是常量;
③自变量可在允许的范围内任意取值.
要点精析
2.求两个变量之间的关系式常用的方法:
(1)利用公式:如图形的周长公式、面积公式、体积公式等;
(2)利用生活中特定的数量关系,如行程问题中“路程=时间×
速度”,销售问题中“销售额=单价×数量”等;
(3)根据表格与图象中的信息列关系式(这种方法以后会学习)等.
要点精析
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
r
h
思考
r指的是底面圆的半径,h指的是圆锥的高.
圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
圆锥的底面半径的长度是自变量;
圆锥的体积是因变量
做一做
(2)如果圆锥底面半径为 r(cm),那么圆锥的体积V(cm3)与r的关系式为________.
(3)当底面半径由1cm变化到10cm时,圆锥的体积由 cm3变化到 cm3 .
你知道什么是“低碳生活”吗?“低碳生
活” 是指人们生活中尽量减少所耗能量,从而
降低 碳(特别是二氧化碳)的排放量的一种式.
(1)家居用电的二氧化碳排放量可以用关系式表示为_____________,其中的字母分别表示 ______________________________.
y=0.785x
二氧化碳排放量,耗电量
议一议
(2)在上述关系式中,耗电量每增加1 KW·h,二氧化碳排放量增加___________.当耗电量从1 KW·h增加到100KW·h时,二氧化碳排放量从_________增加到_________.
0.785 kg
78.5 kg
0.785 kg
家居用电的二氧化碳:
110×0.785=86.35(kg)
开私家车的二氧化碳:
75×2.7=202.5(kg)
家用天然气的二氧化碳:
20×0.19=3.8(kg)
家用自来水的二氧化碳:
5×0.91=4.55(kg)
(3)小明家本月用电大约110 kW·h、天然气20 m3、自来水5 t、油耗75 L,请你计算一下小明家这几项的二氧化碳排放量.
优点:简单明了,能准确反映整个变化过程中自变量与因变量的相互关系.
缺点:求对应值时有时要经过比较复杂的计算,而且实际问题中,有的变量之间的关系不一定能用关系式表示出来.
用关系式表示变量之间的关系的优缺点是什么?
思考
2
1.根据图中的程序,当输入x=3时,输出的结果 y= .
随堂练习
2.在地球某地,温度T(℃)与海拔高度d(m)的关系可以近似地用T=10-
来表示. 根据这个关系式,当d的值分别是0,200,400,600,800,
1000时,计算相应的T值,并用表格表示所得结果.
解:用表格表示所得结果如下:
高度d/m 0 200 400 600 800 1000
温度T/℃ 10.0 8.7 7.3 6.0 4.7 3.3
3.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化中,自变量和因变量各是什么?
(2)写出圆柱的体积V与高h之间的关系式.
自变量是圆柱的高,因变量是圆柱的体积.
V=πr2h= =πh
(3)当h由10 cm变化到5 cm时,V是怎样变化的?
(4)当h=0时,V等于多少?此时表示什么?
当h=10cm时,V=πh=10π cm3;
当h=5cm时,V=πh=5π cm3.
所以当h由10cm变化到5cm时,
V从10π cm3变化到5π cm3.
V=0,此时表示平面图形——直径为2cm的圆.
关系式是用含自变量的代数式表示因变量的等式.
利用关系式表示变量之间的关系,最大的优点在于能比较方便地求出自变量为取值范围内的任意一个值时,相对应的因变量的值.
利用关系式求因变量的值,实际上就是求代数式的值
关系式表示变量间的关系
关系式是用含自变量的代数式表示因变量的等式.
利用关系式表示变量之间的关系,最大的优点在于能比较方便地求出自变量为取值范围内的任意一个值时,相对应的因变量的值.
利用关系式求因变量的值,实际上就是求代数式的值
课堂小结
3.2 用关系式表示的变量间关系
七年级下
北师版
1.能根据具体情景,用关系式表示变量间的关系,并会根据关系式求值,初步体会自变量和因变量的数值对应关系.
2.能将具体问题抽象成数学问题并将它用关系式表示出来.
难点
重点
学习目标
在上节课的“小车下滑的时间”实验中,
新课引入
①支撑物的高度h和小车下滑的时间 t 都在变化,它们都是______.
变量
②其中小车下滑的时间 t 随支撑物的高度 h 的变化而______.
变化
③支撑物的高度 h 是_______,小车下滑的时间t 是________.
自变量
因变量
数青蛙:
一只青蛙一张嘴,两只眼睛四条腿;两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿;……
1. 青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2. 青蛙的腿数和只数有关系吗?能用数学式表达吗?
有,假设青蛙有a只,则青蛙的眼睛数有y只,则数学表达式为y=2a只.
有,假设青蛙有a只,则青蛙的腿数有b只,则数学表达式为b=4a只.
y=2a和b=4a就是用数学表达式表示的变量之间的关系,也是我们本节课要学习的主要内容.
确定一个三角形面积的量有哪些?
D
B
C
A
所以确定三角形面积的量就是三角形
的底边长和对应高
新知学习
S = ah
1
2
因为三角形的面积公式为
想一想
如图,△ABC底边BC上的高是6 cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量和因变量分别是什么?
三角形的底边长度是自变量,
三角形的面积是因变量.
探究
(2)如果三角形的底边长为 x(厘米),那么三角形的面积 y(cm2)可以表示为________.
y=3x
(3)当底边长从12厘米变化到3厘米时,三角形的面积从_____cm2变化到_____cm2.
36
9
y=3x表示的是什么?
y = 3 x
因变量
含自变量代数式
自变量的取值要符合实际
思考
用来表示自变量和因变量之间关系的等式叫做关系式,利用关系式,如y=3x,我们可以根据任何一个自变量值求出相应的因变量的值.
注意:关系式是一个等式;通常把因变量写在等号的左边,含有自变量的代数式写在等号的右边.
归纳
1.关系式的基本特征是:
①等式的左边是因变量,等式的右边是关于自变量的代数式
②等式中只含有自变量和因变量这两个变量,其他的量都是常量;
③自变量可在允许的范围内任意取值.
要点精析
2.求两个变量之间的关系式常用的方法:
(1)利用公式:如图形的周长公式、面积公式、体积公式等;
(2)利用生活中特定的数量关系,如行程问题中“路程=时间×
速度”,销售问题中“销售额=单价×数量”等;
(3)根据表格与图象中的信息列关系式(这种方法以后会学习)等.
要点精析
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
r
h
思考
r指的是底面圆的半径,h指的是圆锥的高.
圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
圆锥的底面半径的长度是自变量;
圆锥的体积是因变量
做一做
(2)如果圆锥底面半径为 r(cm),那么圆锥的体积V(cm3)与r的关系式为________.
(3)当底面半径由1cm变化到10cm时,圆锥的体积由 cm3变化到 cm3 .
你知道什么是“低碳生活”吗?“低碳生
活” 是指人们生活中尽量减少所耗能量,从而
降低 碳(特别是二氧化碳)的排放量的一种式.
(1)家居用电的二氧化碳排放量可以用关系式表示为_____________,其中的字母分别表示 ______________________________.
y=0.785x
二氧化碳排放量,耗电量
议一议
(2)在上述关系式中,耗电量每增加1 KW·h,二氧化碳排放量增加___________.当耗电量从1 KW·h增加到100KW·h时,二氧化碳排放量从_________增加到_________.
0.785 kg
78.5 kg
0.785 kg
家居用电的二氧化碳:
110×0.785=86.35(kg)
开私家车的二氧化碳:
75×2.7=202.5(kg)
家用天然气的二氧化碳:
20×0.19=3.8(kg)
家用自来水的二氧化碳:
5×0.91=4.55(kg)
(3)小明家本月用电大约110 kW·h、天然气20 m3、自来水5 t、油耗75 L,请你计算一下小明家这几项的二氧化碳排放量.
优点:简单明了,能准确反映整个变化过程中自变量与因变量的相互关系.
缺点:求对应值时有时要经过比较复杂的计算,而且实际问题中,有的变量之间的关系不一定能用关系式表示出来.
用关系式表示变量之间的关系的优缺点是什么?
思考
2
1.根据图中的程序,当输入x=3时,输出的结果 y= .
随堂练习
2.在地球某地,温度T(℃)与海拔高度d(m)的关系可以近似地用T=10-
来表示. 根据这个关系式,当d的值分别是0,200,400,600,800,
1000时,计算相应的T值,并用表格表示所得结果.
解:用表格表示所得结果如下:
高度d/m 0 200 400 600 800 1000
温度T/℃ 10.0 8.7 7.3 6.0 4.7 3.3
3.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化中,自变量和因变量各是什么?
(2)写出圆柱的体积V与高h之间的关系式.
自变量是圆柱的高,因变量是圆柱的体积.
V=πr2h= =πh
(3)当h由10 cm变化到5 cm时,V是怎样变化的?
(4)当h=0时,V等于多少?此时表示什么?
当h=10cm时,V=πh=10π cm3;
当h=5cm时,V=πh=5π cm3.
所以当h由10cm变化到5cm时,
V从10π cm3变化到5π cm3.
V=0,此时表示平面图形——直径为2cm的圆.
关系式是用含自变量的代数式表示因变量的等式.
利用关系式表示变量之间的关系,最大的优点在于能比较方便地求出自变量为取值范围内的任意一个值时,相对应的因变量的值.
利用关系式求因变量的值,实际上就是求代数式的值
关系式表示变量间的关系
关系式是用含自变量的代数式表示因变量的等式.
利用关系式表示变量之间的关系,最大的优点在于能比较方便地求出自变量为取值范围内的任意一个值时,相对应的因变量的值.
利用关系式求因变量的值,实际上就是求代数式的值
课堂小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
