4.5 利用三角形全等测距离课件(共22张PPT)
文档属性
| 名称 | 4.5 利用三角形全等测距离课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1008.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:35:11 | ||
图片预览








文档简介
(共22张PPT)
4.5 利用三角形全等测距离
七年级下
北师版
1.会利用三角形全等解决实际问题,体会数学与实际生活的联系.
2.能从实例中构建全等三角形,体会转化思想.
3.在利用三角形全等解决问题的过程中能进行有条理的表达.
学习目标
难点
重点
一位经历过战争的老人讲述的一个故事:
在一次战役中,为了炸毁与我军阵地隔河相望的敌军碉堡,需要测出我军阵地到敌军碉堡的距离.由于没有任何测量工具,我军战士为此绞尽脑汁,这时一位聪明的战士想出了一个办法,为成功炸毁碉堡立了一功.
新课引入
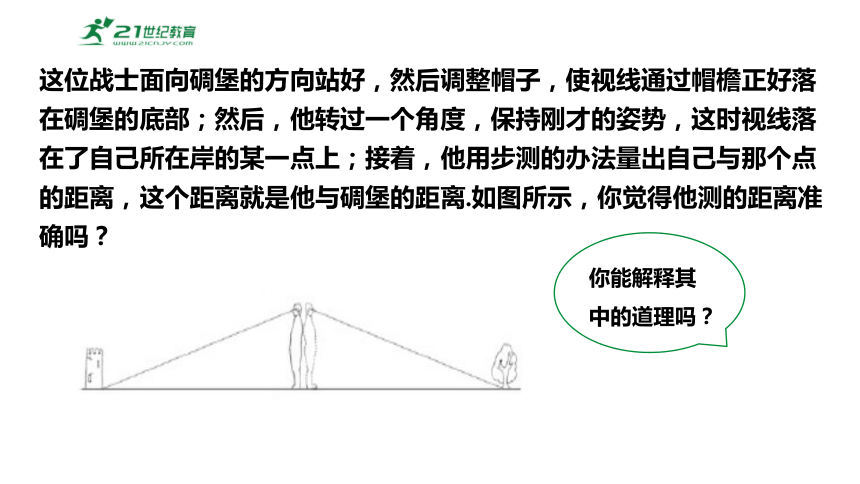
这位战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离.如图所示,你觉得他测的距离准确吗?
你能解释其中的道理吗?
探究
F
E
D
C
B
A
新知学习
由战士所讲述的方法可知:战士的身高CB(FE)不变,战士与地面是垂直的(CB⊥AB,FE⊥ED);视角∠BCA=∠EFD,战士要测的是敌碉堡(A)与我军阵地(B)的距离,战士的结论是只要按要求(如图)测得ED的长度即可.(即AB=ED)
(1)战士所讲述的方法中,已知条件是什么?
F
E
D
C
B
A
碉堡距离
步测距离
∴AB= DE(全等三角形的对应边相等 )
解:在△ABC与△DEF中,
∠BCA=∠EFD
BC=EF(公共边)
∠ABC=∠DEF=90°
∴△ABC≌△DEF(ASA)
(2)请用所学的数学知识说明AB= DE的理由.
利用三角形全等可以测量两点之间的距离.
利用三角形全等测距离,实际上是构造出全等三角形,运用全等三角形的性质(对应边相等),把较难测量的距离转化为较容易测量的线段的长度.
归纳总结
如图,一条输电线路需跨越一个池塘,池塘两侧A,B处各立有一根电线杆,但利用现有皮尺无法直接量出A,B间的距离.请你设计一个方案,测出A,B间的距离,并说明理由.
想一想
A
B
先在地上取一个可以直接到达 A 和 B 点的点 C;
C
E
D
连接 AC 并延长到 D,使CD = AC;连接 BC 并延长到E,使 CE = CB,
连接 DE 并测量出它的长度即为AB 之间的距离.
方案一:
解:理由如下:
∵在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),
∴AB=DE.
CB=CE,
∠ACB=∠DCE,
AC=DC,
A
B
C
E
D
A
B
C
D
方案二:
如图,先作三角形 ABC ,再找一点 D,使AD∥BC,并使AD = BC,连结 CD,量CD 的长即得 AB 之间的距离.
解:理由: 在△DAC与△BCA 中,
所以△DAC ≌ △BCA(SAS)
AB = CD
(全等三角形的对应边相等)
∠DAC = ∠BCA
DA = BC
AC = CA
因为
A
B
C
D
如图,找一点D,使AD⊥BD,延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长.
B
A
D
C
解:连接AB.
在Rt△ADB与Rt△CDB中
所以△ADB≌△CDB(SAS).
所以BA =BC.
BD=BD,
∠ADB=∠CDB,
AD=CD,
方案三:
归纳
由于两个三角形全等,对应边相等,因此利用全等三角形可以解决不能到达或不能直接测量的两点之间的距离问题.解题的关键是构造两个全等三角形,其根据是全等三角形的对应边相等.
方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
1.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A、AO=CO
B、BO=DO
C、AC=BD
D、AO=CO且BO=DO
O
D
C
B
A
D
随堂练习
D
2.如图,某校学生为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,那么他们还应做什么才能测得A,B之间的距离?( )
A.直接测量BM
B.测量BC
C.测量∠A的度数
D.作∠BCN=40°交MB于点N
3.如图,要测量河岸相对的两点A,B之间的距离,先从B处出发,沿与AB成90°角方向,向前走50 m到C处立一根标杆,然后保持方向不变,继续朝前走50 m到D处,在D处转90°沿DE方向再走17 m到达E处,使A,C与E在同一直线上,那么测得A,B之间的距离为________m.
17
4.如图,有两个滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF
相等,左边滑梯水平方向的长度AB与右边滑梯的高度DE相等,测得
BC=2.5 m,则EF= .
2.5 m
5.小明想用绳子测量湖A、B之间的距离,但绳子不够长,又没有船可载他往来A、B之间.他怎样才能测出A、B之间的距离呢?把你的设计方案在图上画出来,并与你的同伴交流不同的方法.
●
●
A
B
方法一:
在能够到达A、B的空地上取一适当点C,连接AC,并延长AC到D,使CD=AC,连接BC,并延长BC到E,使CE=BC,连接ED.则只要测出ED的长就可以知道AB的长了.
理由如下: 在ΔACB与ΔDCE中,
∠BCA=∠ECD
AC= DC
BC=CE
∴ΔACB≌ΔDCE(SAS)
∴AB=DE(全等三角形的对应边相等)
●
●
A
B
C
D
E
方法二:
在AB的垂线BF上取两点C、D,使CD=BC.再过D点作出BF的垂线DG,并在DG上找一点E,使A、C、E在一条直线上.这时测得的DE的长就是A 、B间距离.
F
D
E
C
A
B
G
理由如下:在△ACB与△ECD中,
∠ABC=∠EDC=90°
BC=DC
∠ACB=∠ECD
∴△ACB≌△ECD ( ASA)
∴AB=DE( 全等三角形的对应边相等)
由于两个三角形全等,对应边相等,因此利用全等三角形可以解决不能到达或不能直接测量的两点之间的距离问题.解题的关键是构造两个全等三角形,其根据是全等三角形的对应边相等.
利用三角形全等测距离
课堂小结
4.5 利用三角形全等测距离
七年级下
北师版
1.会利用三角形全等解决实际问题,体会数学与实际生活的联系.
2.能从实例中构建全等三角形,体会转化思想.
3.在利用三角形全等解决问题的过程中能进行有条理的表达.
学习目标
难点
重点
一位经历过战争的老人讲述的一个故事:
在一次战役中,为了炸毁与我军阵地隔河相望的敌军碉堡,需要测出我军阵地到敌军碉堡的距离.由于没有任何测量工具,我军战士为此绞尽脑汁,这时一位聪明的战士想出了一个办法,为成功炸毁碉堡立了一功.
新课引入
这位战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离.如图所示,你觉得他测的距离准确吗?
你能解释其中的道理吗?
探究
F
E
D
C
B
A
新知学习
由战士所讲述的方法可知:战士的身高CB(FE)不变,战士与地面是垂直的(CB⊥AB,FE⊥ED);视角∠BCA=∠EFD,战士要测的是敌碉堡(A)与我军阵地(B)的距离,战士的结论是只要按要求(如图)测得ED的长度即可.(即AB=ED)
(1)战士所讲述的方法中,已知条件是什么?
F
E
D
C
B
A
碉堡距离
步测距离
∴AB= DE(全等三角形的对应边相等 )
解:在△ABC与△DEF中,
∠BCA=∠EFD
BC=EF(公共边)
∠ABC=∠DEF=90°
∴△ABC≌△DEF(ASA)
(2)请用所学的数学知识说明AB= DE的理由.
利用三角形全等可以测量两点之间的距离.
利用三角形全等测距离,实际上是构造出全等三角形,运用全等三角形的性质(对应边相等),把较难测量的距离转化为较容易测量的线段的长度.
归纳总结
如图,一条输电线路需跨越一个池塘,池塘两侧A,B处各立有一根电线杆,但利用现有皮尺无法直接量出A,B间的距离.请你设计一个方案,测出A,B间的距离,并说明理由.
想一想
A
B
先在地上取一个可以直接到达 A 和 B 点的点 C;
C
E
D
连接 AC 并延长到 D,使CD = AC;连接 BC 并延长到E,使 CE = CB,
连接 DE 并测量出它的长度即为AB 之间的距离.
方案一:
解:理由如下:
∵在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),
∴AB=DE.
CB=CE,
∠ACB=∠DCE,
AC=DC,
A
B
C
E
D
A
B
C
D
方案二:
如图,先作三角形 ABC ,再找一点 D,使AD∥BC,并使AD = BC,连结 CD,量CD 的长即得 AB 之间的距离.
解:理由: 在△DAC与△BCA 中,
所以△DAC ≌ △BCA(SAS)
AB = CD
(全等三角形的对应边相等)
∠DAC = ∠BCA
DA = BC
AC = CA
因为
A
B
C
D
如图,找一点D,使AD⊥BD,延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长.
B
A
D
C
解:连接AB.
在Rt△ADB与Rt△CDB中
所以△ADB≌△CDB(SAS).
所以BA =BC.
BD=BD,
∠ADB=∠CDB,
AD=CD,
方案三:
归纳
由于两个三角形全等,对应边相等,因此利用全等三角形可以解决不能到达或不能直接测量的两点之间的距离问题.解题的关键是构造两个全等三角形,其根据是全等三角形的对应边相等.
方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
1.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A、AO=CO
B、BO=DO
C、AC=BD
D、AO=CO且BO=DO
O
D
C
B
A
D
随堂练习
D
2.如图,某校学生为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,那么他们还应做什么才能测得A,B之间的距离?( )
A.直接测量BM
B.测量BC
C.测量∠A的度数
D.作∠BCN=40°交MB于点N
3.如图,要测量河岸相对的两点A,B之间的距离,先从B处出发,沿与AB成90°角方向,向前走50 m到C处立一根标杆,然后保持方向不变,继续朝前走50 m到D处,在D处转90°沿DE方向再走17 m到达E处,使A,C与E在同一直线上,那么测得A,B之间的距离为________m.
17
4.如图,有两个滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF
相等,左边滑梯水平方向的长度AB与右边滑梯的高度DE相等,测得
BC=2.5 m,则EF= .
2.5 m
5.小明想用绳子测量湖A、B之间的距离,但绳子不够长,又没有船可载他往来A、B之间.他怎样才能测出A、B之间的距离呢?把你的设计方案在图上画出来,并与你的同伴交流不同的方法.
●
●
A
B
方法一:
在能够到达A、B的空地上取一适当点C,连接AC,并延长AC到D,使CD=AC,连接BC,并延长BC到E,使CE=BC,连接ED.则只要测出ED的长就可以知道AB的长了.
理由如下: 在ΔACB与ΔDCE中,
∠BCA=∠ECD
AC= DC
BC=CE
∴ΔACB≌ΔDCE(SAS)
∴AB=DE(全等三角形的对应边相等)
●
●
A
B
C
D
E
方法二:
在AB的垂线BF上取两点C、D,使CD=BC.再过D点作出BF的垂线DG,并在DG上找一点E,使A、C、E在一条直线上.这时测得的DE的长就是A 、B间距离.
F
D
E
C
A
B
G
理由如下:在△ACB与△ECD中,
∠ABC=∠EDC=90°
BC=DC
∠ACB=∠ECD
∴△ACB≌△ECD ( ASA)
∴AB=DE( 全等三角形的对应边相等)
由于两个三角形全等,对应边相等,因此利用全等三角形可以解决不能到达或不能直接测量的两点之间的距离问题.解题的关键是构造两个全等三角形,其根据是全等三角形的对应边相等.
利用三角形全等测距离
课堂小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
