5.2 探索轴对称的性质课件(共25张PPT)
文档属性
| 名称 | 5.2 探索轴对称的性质课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
5.2 探索轴对称的性质
七年级下
北师版
1.进一步复习生活中的轴对称现象,探索并掌握轴对称的性质.
2.会利用轴对称的性质作对称点、对称图形、对称轴等.
3.经历丰富材料的学习过程,提高对图形的观察、分析、判断、归纳等能力.
学习目标
难点
重点
复习回顾:
1.如果_____________沿一条直线折叠后,直线两旁的部分能够__________,那么这个图形叫做轴对称图形,这条直线叫做________.
2.如果两个平面图形,沿一条直线对折后能够_________,那么称这两个图形成轴对称,这条直线叫做这两个图形的_________.
一个平面图形
互相重合
对称轴
完全重合
对称轴
新课引入
一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式?”过了很长时间,也没有人答出.
小兰仅仅拿了一面镜子,就很快解决了这道题目.
你知道她是怎样做的吗?
你知道为什么吗?
?
打开
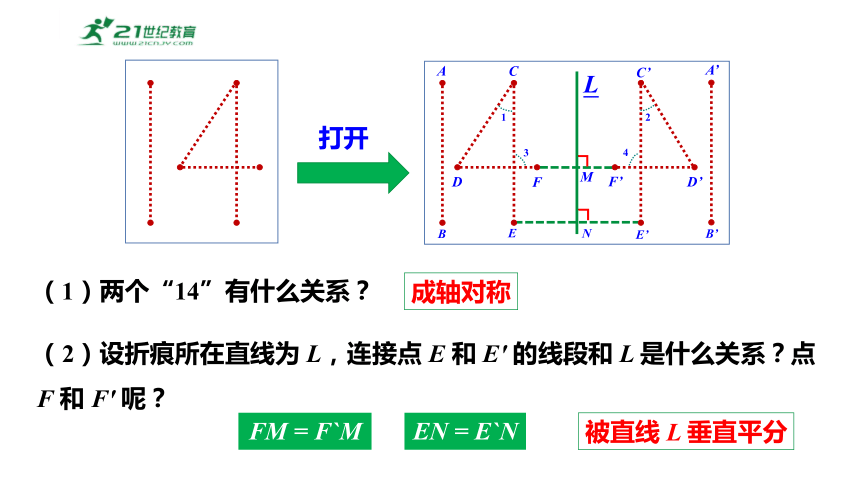
如图:将一张长方形的纸对折,然后用笔扎出“14”这个数字,将纸打开后铺平:
A
A’
B
C
D
E
F
1
2
3
4
C’
E’
F’
D’
B’
新知学习
(1)两个“14”有什么关系?
(2)设折痕所在直线为 L,连接点 E 和 E′ 的线段和 L 是什么关系?点F 和 F′ 呢?
被直线 L 垂直平分
成轴对称
L
M
N
FM = F`M
EN = E`N
打开
A
A’
B
C
D
E
F
1
2
3
4
C’
E’
F’
D’
B’
(3)线段AB与A′B′,CD与C′D′ 有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
AB = A′B′
∠1=∠2
CD = C′D′
∠3=∠4
L
M
N
打开
A
A’
B
C
D
E
F
1
2
3
4
C’
E’
F’
D’
B’
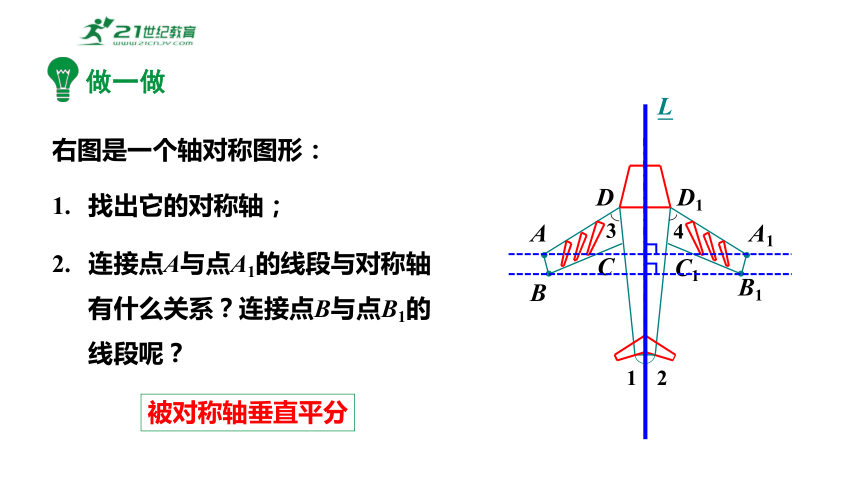
右图是一个轴对称图形:
找出它的对称轴;
连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
A
A1
B
C
D
D1
C1
B1
3
4
1
2
被对称轴垂直平分
L
做一做
线段AD与线段A1D1有什么关系?线段BC与B1C1呢 为什么?
AD = A1D1,BC = B1C1
∠1 = ∠2,∠3 = ∠4
A
A1
B
C
D
D1
C1
B1
3
4
1
2
L
综合以上问题,你能得到什么结论?
思考
∠1与∠2有什么关系 ∠3与∠4呢?说说你的理由.
在轴对称图形中,对应点所连的线段与对称轴有什么关系?对应线段有什么关系?对应角有什么关系?在两个成轴对称的图形中呢?
议一议
在轴对称图形或两个成轴对称的图形中,对应点所连的线段,被对称轴垂直平分,对应线段相等,对应角相等.
例1 画出 ΔABC 关于直线 L 的对称图形.
方法总结
画原图关于某直线对称的图形的步骤:
①找:在原图形上找特殊点(如线段的端点);
②作:作各个特殊点关于对称轴的对称点;
③连:按原图的顺序连接所作的各对称点.
一找二作三连
例2 如图,正方形 ABCD 的边长为 4 cm,则图中阴影部分的面积为 ( )
A.4 cm2 B.8 cm2 C.12 cm2 D.16 cm2
解析:根据正方形的轴对称性,可知阴影部分的面积等于正方形 ABCD 面积的一半.因为正方形 ABCD 的边长为 4 cm,所以 S阴影=42÷2=8 (cm2).
B
如图是一个图案的一半,其中的虚线是这个图案的对称轴,画出这个图案的另一半.
·
·
做一做
例3 用笔尖扎重叠的纸可以得到下面成轴对称的两个图案.
(1)找出它的两组对应点、两条对应线段和两个对应角;
(2)说明你找到的对应点所连线段分别被对称轴垂直平分.
解:如图,点 A 与点 A′ 是一组对应点,点 B 与点 B 是一组对应点;线段 AB 与线段 A′B′ 是对应线段;∠ABC 与∠A′B′C′ 是对应角.
1.两个图形关于某直线对称,对称点一定 ( )
A. 这直线的两旁
B.这直线的同旁
C.这直线上
D.这直线两旁或这直线上
D
随堂练习
2. 如图,△ABC与△DEF 关于直线 l 成轴对称,则以下结论中错误的是 ( )
A. AB∥DF
B. ∠B =∠E
C. AB = DE
D. l 垂直平分 AD
A
3.如图,将矩形ABCD沿DE折叠,使A点落在BC上的F处,若∠EFB=60°,则∠CFD=( )
A.20°
B.30°
C.40°
D.50°
A
B
C
D
E
F
B
4.如图,△ABC 与△DEF 关于直线 l 对称,你有哪些方法画出直线 l ?
5.如图,把下列图形补成关于直线 l 的对称图形.
6. 如图,已知点 P 是∠AOB 内任意一点,点 P1,P 关于 OA 对称,点 P2,P 关于 OB 对称. 连接 P1P2,分别交 OA,OB 于 C,D. 连接 PC,PD. 若 P1P2=10 cm,则△PCD 的周长为 cm.
10
.
.
P2
P
.
P1
C
D
B
A
O
解:∵点 P1,P 关于 OA 对称,且 C 在OA上
∴P1C 和PC也关于 OA 对称
∴P1C =PC
同理可得:PD =P2D
∴C△PCD =PC+CD+PD=P1C+CD+P2D=P1P2=10 cm
在轴对称图形或两个成轴对称的图形中,对应点所连的线段,被对称轴垂直平分,对应线段相等,对应角相等.
探索轴对
称的性质
性质
作图方法
①找:在原图形上找特殊点(如线段的端点);
②作:作各个特殊点关于对称轴的对称点;
③连:按原图的顺序连接所作的各对称点.
课堂小结
5.2 探索轴对称的性质
七年级下
北师版
1.进一步复习生活中的轴对称现象,探索并掌握轴对称的性质.
2.会利用轴对称的性质作对称点、对称图形、对称轴等.
3.经历丰富材料的学习过程,提高对图形的观察、分析、判断、归纳等能力.
学习目标
难点
重点
复习回顾:
1.如果_____________沿一条直线折叠后,直线两旁的部分能够__________,那么这个图形叫做轴对称图形,这条直线叫做________.
2.如果两个平面图形,沿一条直线对折后能够_________,那么称这两个图形成轴对称,这条直线叫做这两个图形的_________.
一个平面图形
互相重合
对称轴
完全重合
对称轴
新课引入
一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式?”过了很长时间,也没有人答出.
小兰仅仅拿了一面镜子,就很快解决了这道题目.
你知道她是怎样做的吗?
你知道为什么吗?
?
打开
如图:将一张长方形的纸对折,然后用笔扎出“14”这个数字,将纸打开后铺平:
A
A’
B
C
D
E
F
1
2
3
4
C’
E’
F’
D’
B’
新知学习
(1)两个“14”有什么关系?
(2)设折痕所在直线为 L,连接点 E 和 E′ 的线段和 L 是什么关系?点F 和 F′ 呢?
被直线 L 垂直平分
成轴对称
L
M
N
FM = F`M
EN = E`N
打开
A
A’
B
C
D
E
F
1
2
3
4
C’
E’
F’
D’
B’
(3)线段AB与A′B′,CD与C′D′ 有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
AB = A′B′
∠1=∠2
CD = C′D′
∠3=∠4
L
M
N
打开
A
A’
B
C
D
E
F
1
2
3
4
C’
E’
F’
D’
B’
右图是一个轴对称图形:
找出它的对称轴;
连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
A
A1
B
C
D
D1
C1
B1
3
4
1
2
被对称轴垂直平分
L
做一做
线段AD与线段A1D1有什么关系?线段BC与B1C1呢 为什么?
AD = A1D1,BC = B1C1
∠1 = ∠2,∠3 = ∠4
A
A1
B
C
D
D1
C1
B1
3
4
1
2
L
综合以上问题,你能得到什么结论?
思考
∠1与∠2有什么关系 ∠3与∠4呢?说说你的理由.
在轴对称图形中,对应点所连的线段与对称轴有什么关系?对应线段有什么关系?对应角有什么关系?在两个成轴对称的图形中呢?
议一议
在轴对称图形或两个成轴对称的图形中,对应点所连的线段,被对称轴垂直平分,对应线段相等,对应角相等.
例1 画出 ΔABC 关于直线 L 的对称图形.
方法总结
画原图关于某直线对称的图形的步骤:
①找:在原图形上找特殊点(如线段的端点);
②作:作各个特殊点关于对称轴的对称点;
③连:按原图的顺序连接所作的各对称点.
一找二作三连
例2 如图,正方形 ABCD 的边长为 4 cm,则图中阴影部分的面积为 ( )
A.4 cm2 B.8 cm2 C.12 cm2 D.16 cm2
解析:根据正方形的轴对称性,可知阴影部分的面积等于正方形 ABCD 面积的一半.因为正方形 ABCD 的边长为 4 cm,所以 S阴影=42÷2=8 (cm2).
B
如图是一个图案的一半,其中的虚线是这个图案的对称轴,画出这个图案的另一半.
·
·
做一做
例3 用笔尖扎重叠的纸可以得到下面成轴对称的两个图案.
(1)找出它的两组对应点、两条对应线段和两个对应角;
(2)说明你找到的对应点所连线段分别被对称轴垂直平分.
解:如图,点 A 与点 A′ 是一组对应点,点 B 与点 B 是一组对应点;线段 AB 与线段 A′B′ 是对应线段;∠ABC 与∠A′B′C′ 是对应角.
1.两个图形关于某直线对称,对称点一定 ( )
A. 这直线的两旁
B.这直线的同旁
C.这直线上
D.这直线两旁或这直线上
D
随堂练习
2. 如图,△ABC与△DEF 关于直线 l 成轴对称,则以下结论中错误的是 ( )
A. AB∥DF
B. ∠B =∠E
C. AB = DE
D. l 垂直平分 AD
A
3.如图,将矩形ABCD沿DE折叠,使A点落在BC上的F处,若∠EFB=60°,则∠CFD=( )
A.20°
B.30°
C.40°
D.50°
A
B
C
D
E
F
B
4.如图,△ABC 与△DEF 关于直线 l 对称,你有哪些方法画出直线 l ?
5.如图,把下列图形补成关于直线 l 的对称图形.
6. 如图,已知点 P 是∠AOB 内任意一点,点 P1,P 关于 OA 对称,点 P2,P 关于 OB 对称. 连接 P1P2,分别交 OA,OB 于 C,D. 连接 PC,PD. 若 P1P2=10 cm,则△PCD 的周长为 cm.
10
.
.
P2
P
.
P1
C
D
B
A
O
解:∵点 P1,P 关于 OA 对称,且 C 在OA上
∴P1C 和PC也关于 OA 对称
∴P1C =PC
同理可得:PD =P2D
∴C△PCD =PC+CD+PD=P1C+CD+P2D=P1P2=10 cm
在轴对称图形或两个成轴对称的图形中,对应点所连的线段,被对称轴垂直平分,对应线段相等,对应角相等.
探索轴对
称的性质
性质
作图方法
①找:在原图形上找特殊点(如线段的端点);
②作:作各个特殊点关于对称轴的对称点;
③连:按原图的顺序连接所作的各对称点.
课堂小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
