人教版七年级下册第五章:相交线与平行线单元测试卷(含答案)
文档属性
| 名称 | 人教版七年级下册第五章:相交线与平行线单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 614.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-11 18:01:50 | ||
图片预览


文档简介
登录二一教育在线组卷平台 助您教考全无忧
人教版七年级下册第五章:相交线与平行线单元测试卷
时间90分钟分 分值100分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题
得分
1.如图,与∠1是同旁内角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,直线a,b被直线c所截,.若,则的度数是( )
A. B. C. D.
3.如图所示,直线,相交于点,于点,且,则的度数是( )
A. B. C. D.
4.如图,,若,则的度数是( )
A. B. C. D.
5.将一个直角三角板和一把直尺按如图所示摆放,若,则的度数为( )
A. B. C. D.
6.下列命题中,是真命题的是( )
A.两直线平行,同旁内角互补
B.相等的角是对顶角
C.a,b,c是直线,若,,则
D.内错角相等
7.如图,在四边形中,,将四边形沿折叠后,C,D两点分别落在,上,若,则的大小是( )
A. B. C. D.
8.如图,点A,O,B在同一条直线上,若,则的度数是( )
A. B. C. D.
9.下列说法中正确的有( )
①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③在同一平面内,垂直于同一条的直线的两条直线互相平行;④两条平行线被第三条直线所截,一对同旁内角的平分线互相垂直.
A.①③ B.①④ C.②③ D.③④
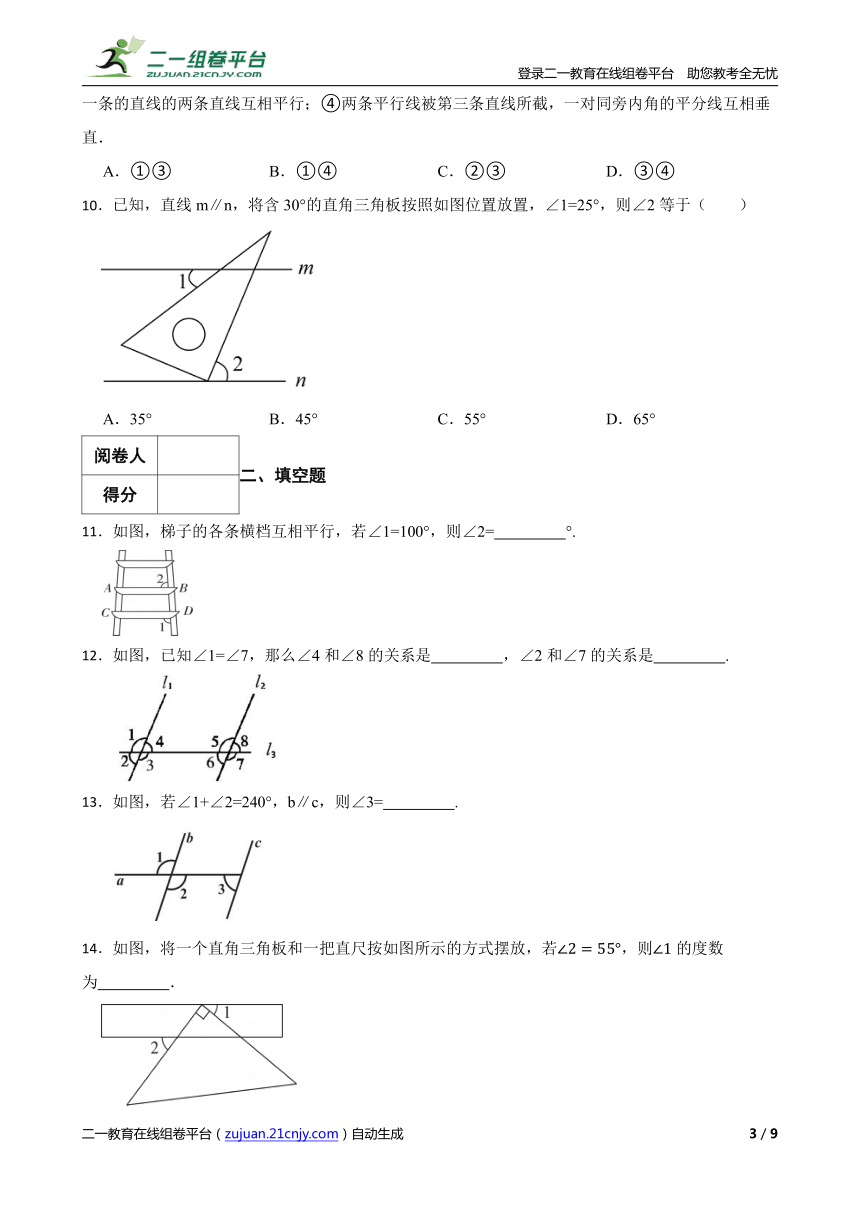
10.已知,直线m∥n,将含30°的直角三角板按照如图位置放置,∠1=25°,则∠2等于( )
A.35° B.45° C.55° D.65°
阅卷人 二、填空题
得分
11.如图,梯子的各条横档互相平行,若∠1=100°,则∠2= °.
12.如图,已知∠1=∠7,那么∠4和∠8的关系是 ,∠2和∠7的关系是 .
13.如图,若∠1+∠2=240°,b∥c,则∠3= .
14.如图,将一个直角三角板和一把直尺按如图所示的方式摆放,若,则的度数为 .
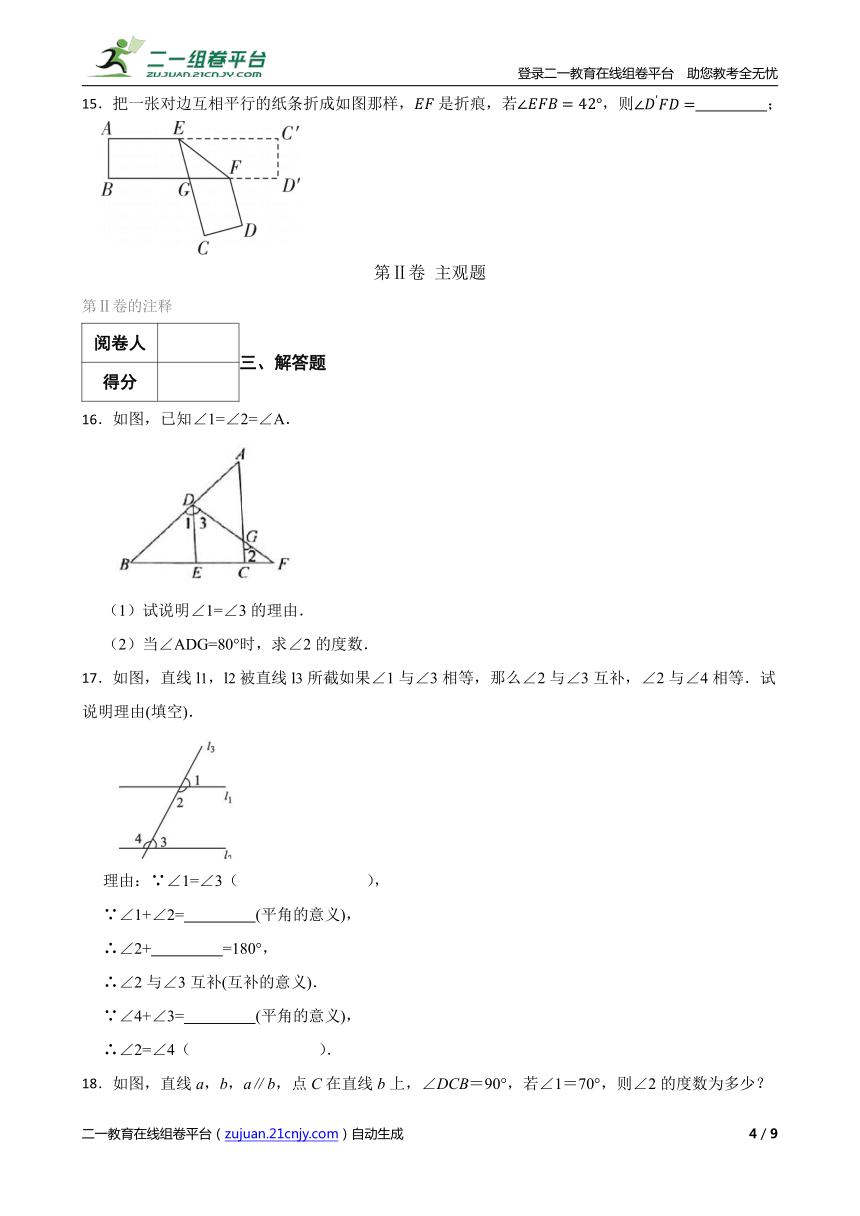
15.把一张对边互相平行的纸条折成如图那样,是折痕,若,则 ;
第Ⅱ卷 主观题
第Ⅱ卷的注释
阅卷人 三、解答题
得分
16.如图,已知∠1=∠2=∠A.
(1)试说明∠1=∠3的理由.
(2)当∠ADG=80°时,求∠2的度数.
17.如图,直线l1,l2被直线l3所截如果∠1与∠3相等,那么∠2与∠3互补,∠2与∠4相等.试说明理由(填空).
理由:∵∠1=∠3( ),
∵∠1+∠2= (平角的意义),
∴∠2+ =180°,
∴∠2与∠3互补(互补的意义).
∵∠4+∠3= (平角的意义),
∴∠2=∠4( ).
18.如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为多少?
19.如图,已知,.
求证:.
请完善证明过程,在括号内填写相应的理论依据.
证明:已知,
,
,
,
,
,
,
▲ ,
20.如图,直线相交于点O,,.求与的度数.
21.如图,直线与相交于点O,,垂足为O.
(1)若,则 °;
(2)若,求的度数.
22.已知:如图,∠1和∠2互为补角,∠A=∠D,求证AB∥CD.
23.如图,分别与、相交于点、点,,,则与平行吗?请说明理由.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】C
11.【答案】80
12.【答案】相等;互补
13.【答案】60°
14.【答案】35°
15.【答案】
16.【答案】(1)解:∵ ∠1=∠A,
∴AC∥DE,
∴ ∠3=∠2,
∵ ∠1=∠2,
∴ ∠1=∠3;
(2)解:∵ ∠ADG=80° ,∠ADG+∠BDG=180°,
∴∠BDG=100°,
∴∠1=∠3=50°,
∵AC∥DE,
∴∠2=∠3=50°.
17.【答案】180°;∠3;180°
18.【答案】解:∵∠1=70°,∠1与∠3是对顶角,
∴∠3=∠1=70°.
∵a∥b,点C在直线b上,∠DCB=90°,
∴∠2+∠DCB+∠3=180°,
∴∠2=180°-∠3-∠DCB=180°-70°-90°=20°.
19.【答案】解:已知,
对顶角相等,
,
同旁内角互补,两直线平行,
两直线平行,内错角相等,
,
等量代换,
同位角相等,两直线平行,
两直线平行,同位角相等.
20.【答案】解:∵,
∴,
∵,
∴,
∴.
21.【答案】(1)60
(2)解:∵,
∴.
∵,
∴设,,则,
解得,
∴,
∴.
22.【答案】证明:
∵∠1+∠2=180°(已知),
又∵∠1=∠3(对顶角相等),
∴∠2+∠3=180°,
∴AE∥DF(同旁内角互补,两直线平行),
∴∠4=∠D(两直线平行,同位角相等),
∵∠A=∠D(已知)
∴∠4=∠A(等量代换)
∴AB∥CD(内错角相等,两直线平行),
23.【答案】结论:,
证明:∵,,
∴,
∴;
∴.
∵,
∴,
∴.
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
人教版七年级下册第五章:相交线与平行线单元测试卷
时间90分钟分 分值100分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题
得分
1.如图,与∠1是同旁内角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,直线a,b被直线c所截,.若,则的度数是( )
A. B. C. D.
3.如图所示,直线,相交于点,于点,且,则的度数是( )
A. B. C. D.
4.如图,,若,则的度数是( )
A. B. C. D.
5.将一个直角三角板和一把直尺按如图所示摆放,若,则的度数为( )
A. B. C. D.
6.下列命题中,是真命题的是( )
A.两直线平行,同旁内角互补
B.相等的角是对顶角
C.a,b,c是直线,若,,则
D.内错角相等
7.如图,在四边形中,,将四边形沿折叠后,C,D两点分别落在,上,若,则的大小是( )
A. B. C. D.
8.如图,点A,O,B在同一条直线上,若,则的度数是( )
A. B. C. D.
9.下列说法中正确的有( )
①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③在同一平面内,垂直于同一条的直线的两条直线互相平行;④两条平行线被第三条直线所截,一对同旁内角的平分线互相垂直.
A.①③ B.①④ C.②③ D.③④
10.已知,直线m∥n,将含30°的直角三角板按照如图位置放置,∠1=25°,则∠2等于( )
A.35° B.45° C.55° D.65°
阅卷人 二、填空题
得分
11.如图,梯子的各条横档互相平行,若∠1=100°,则∠2= °.
12.如图,已知∠1=∠7,那么∠4和∠8的关系是 ,∠2和∠7的关系是 .
13.如图,若∠1+∠2=240°,b∥c,则∠3= .
14.如图,将一个直角三角板和一把直尺按如图所示的方式摆放,若,则的度数为 .
15.把一张对边互相平行的纸条折成如图那样,是折痕,若,则 ;
第Ⅱ卷 主观题
第Ⅱ卷的注释
阅卷人 三、解答题
得分
16.如图,已知∠1=∠2=∠A.
(1)试说明∠1=∠3的理由.
(2)当∠ADG=80°时,求∠2的度数.
17.如图,直线l1,l2被直线l3所截如果∠1与∠3相等,那么∠2与∠3互补,∠2与∠4相等.试说明理由(填空).
理由:∵∠1=∠3( ),
∵∠1+∠2= (平角的意义),
∴∠2+ =180°,
∴∠2与∠3互补(互补的意义).
∵∠4+∠3= (平角的意义),
∴∠2=∠4( ).
18.如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为多少?
19.如图,已知,.
求证:.
请完善证明过程,在括号内填写相应的理论依据.
证明:已知,
,
,
,
,
,
,
▲ ,
20.如图,直线相交于点O,,.求与的度数.
21.如图,直线与相交于点O,,垂足为O.
(1)若,则 °;
(2)若,求的度数.
22.已知:如图,∠1和∠2互为补角,∠A=∠D,求证AB∥CD.
23.如图,分别与、相交于点、点,,,则与平行吗?请说明理由.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】C
11.【答案】80
12.【答案】相等;互补
13.【答案】60°
14.【答案】35°
15.【答案】
16.【答案】(1)解:∵ ∠1=∠A,
∴AC∥DE,
∴ ∠3=∠2,
∵ ∠1=∠2,
∴ ∠1=∠3;
(2)解:∵ ∠ADG=80° ,∠ADG+∠BDG=180°,
∴∠BDG=100°,
∴∠1=∠3=50°,
∵AC∥DE,
∴∠2=∠3=50°.
17.【答案】180°;∠3;180°
18.【答案】解:∵∠1=70°,∠1与∠3是对顶角,
∴∠3=∠1=70°.
∵a∥b,点C在直线b上,∠DCB=90°,
∴∠2+∠DCB+∠3=180°,
∴∠2=180°-∠3-∠DCB=180°-70°-90°=20°.
19.【答案】解:已知,
对顶角相等,
,
同旁内角互补,两直线平行,
两直线平行,内错角相等,
,
等量代换,
同位角相等,两直线平行,
两直线平行,同位角相等.
20.【答案】解:∵,
∴,
∵,
∴,
∴.
21.【答案】(1)60
(2)解:∵,
∴.
∵,
∴设,,则,
解得,
∴,
∴.
22.【答案】证明:
∵∠1+∠2=180°(已知),
又∵∠1=∠3(对顶角相等),
∴∠2+∠3=180°,
∴AE∥DF(同旁内角互补,两直线平行),
∴∠4=∠D(两直线平行,同位角相等),
∵∠A=∠D(已知)
∴∠4=∠A(等量代换)
∴AB∥CD(内错角相等,两直线平行),
23.【答案】结论:,
证明:∵,,
∴,
∴;
∴.
∵,
∴,
∴.
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
