7.3三元一次方程组的解法 课件(共24张PPT)
文档属性
| 名称 | 7.3三元一次方程组的解法 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 891.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
7.3 三元一次方程组的解法
七年级下
华师版
1. 了解三元一次方程组的概念,会解三元一次方程组,体会消元的思路,提高分析能力,计算能力.
2. 经过探索三元一次方程组的解法的过程,理解代入消元法和加减消元法所体现的化未知为已知的化归的思想方法.
学习目标
重点
难点
小明、小兰、小红三个人的年龄的和是 26 岁,小明比小兰大 1 岁,小明年龄的两倍与小红的年龄之和比小兰大 18 岁.
如何求三个小动物的年龄?
新课引入
根据题意,设小明、小兰、小红的年龄分别为 x岁、y岁、z岁, 可以列出以下三个方程:
x + y + z = 26,
x – y = 1,
2x + z – y = 18.
那么这三个方程的组合我们该如何称呼?又该如何去解未知数的值呢?这就是我们本节课要学习的内容.
在前面的课程中,我们应用二元一次方程组,求出了勇士队在“我们的小世界杯”足球赛第一轮比赛中胜与平的场数.
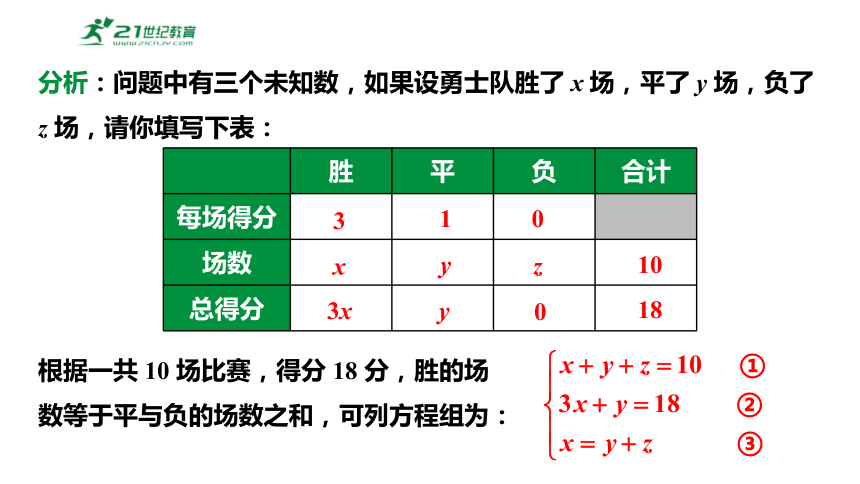
在第二轮比赛中,勇士队参加了 10 场比赛,按同样的计分规则,共得 18 分,已知勇士队在比赛中胜的场数正好等于平与负的场数之和,那么勇士队在第二轮比赛中,胜、负、平的场数各是多少?
新知学习
分析:问题中有三个未知数,如果设勇士队胜了 x 场,平了 y 场,负了 z 场,请你填写下表:
胜 平 负 合计
每场得分
场数
总得分
3
1
0
x
y
z
3x
y
0
10
18
根据一共 10 场比赛,得分 18 分,胜的场数等于平与负的场数之和,可列方程组为:
思考
1. 类比二元一次方程,上述方程组中每个方程都是 __________ 方程.
2. 上面的方程组应该叫做 __________ 方程组.
一次
三元一次
解:方程组
把 ③ 代入 ①②,整理得
解得
将其代入③得 x = 5.
所以
思考
上面的三元一次方程组能否用加减消元法求解?或者能否利用方程 ③,直接消去方程 ① 中的 y + z?比较一下,哪种方法更简便?
① + ③ 得,x + y + z + x = 10 + y + z
即 2x = 10
解得 x = 5.
例1 解方程:
解:由 ② 得 z = 7 - 3x + 2y ④,
把 ④ 代入 ① 和 ③,得
整理,得
解得
代入④,得 z = 7 - 3 - 6 = -2.
所以原方程组的解是
归纳
这里,我们用的是代入消元法:先由方程 ②,用含有 x、y 的代数式表示 z,再分别代入方程 ① 和方程 ③,消去未知数 z,转化为只含有 x、y 的二元一次方程组求解.
例2 解方程:
解:由③ - ②,得 3x + 6z = -24,即 x + 2z = -8.
①×3 + ②×4,得 17x - 17z = 17,即 x - z = 1.
得方程组 ,
解得
代入②,得 y = 0.
所以原方程的解为
归纳
上述例 1 和例 2 的解答分别应用了代入消元法和加减消元法,先消去某一个未知数,将三元一次方程组转化为二元一次方程组,然后解所得的方程组,得到 2 个未知数的值,进而求出第三个未知数的值,从而得到方程的解.
例3 解方程组
x + y + z = 2 ①
x – y + z = 0 ②
x – z = 4 ③
分析:1. 化“三元”为“二元”
考虑消去哪个未知数 ( 也就是三个未知数要去掉哪一个?)
解法一:消去 y,① + ② 得
x + z = 1 ④
联立 ③ 得
x – z = 4 ③
x + z = 1 ④
x + y + z = 2 ①
x – y + z = 0 ②
x – z = 4 ③
解法二:消去 x, 由 ③ 得 x = z + 4 ④
把 ④ 代入 ①、② 得,
(z + 4) + y + z = 2 ⑤
(z + 4) - y + z = 0 ⑥
化简得,
2z + y = -2, ⑦
2z - y = -4. ⑧
x + y + z = 2 ①
x – y + z = 0 ②
x – z = 4 ③
解法三:消去 z,由 ③ 得,z = x - 4 ④
把 ④ 代入 ①、② 得
x + y + (x - 4) = 2, ⑤
x - y + (x - 4) = 0. ⑥
化简得,
2x + y = 6, ⑦
2x - y = 4. ⑧
x + y + z = 2 ①
x – y + z = 0 ②
x – z = 4 ③
解:① + ② 得
x + z = 1 ④
联立 ③ 得
x – z = 4 ③
x + z = 1 ④
③ + ④,得 2x = 5
所以,原方程的解是
x =
y = 1
z =
例4 解方程组
x + y = 3 ①
y + z = 5 ②
z + x = 4 ③
解:③ - ②,得 x - y = -1 ④
① + ④,得 2x = 2
∴x = 1.
把 x = 1 代入方程 ①、③,分别得
y = 2,z = 3
x = 1,
所以,原方程组的解是 y = 2,
z = 3 .
例4 解方程组
x + y = 3 ①
y + z = 5 ②
z + x = 4 ③
例4 也可以这样解:
① + ② + ③ 得 2(x + y + z ) = 12 ④
即,x + y + z = 6 ⑤
⑤ - ①,得 z = 3
⑤ - ②,得 x = 1
⑤ - ③,得 y = 2
所以,原方程组的解是 x = 1,
y = 2,
z = 3 .
1. 解三元一次方程组的基本思路是什么?
消元,转化
三元一次方程组
二元一次方程组
转化
一元一次方程
转化
2. 在三元化二元时,对于具体方法的选取应该注意什么?
求解三元一次方程组:
观察
消元
代入消元
加减消元
力求简便
归纳
x + y + z = 12 ①
x + 2y + 5z = 22 ②
x = 4y ③
1. 解方程组
解:将 x = 4y 代入 ①、②.
4y + y + z = 12 ④
4y + 2y + 5z = 22 ⑤
化简得:
5y + z = 12 ⑥
6y + 5z = 22 ⑦
⑥×5 - ⑦,得 19y = 38
即 y = 2.
所以,原方程的解是
x = 8
y = 2
z = 2
随堂练习
2. 若 x+2y+3z = 10,4x+3y+2z = 15,则 x+y+z 的值为( )
A. 2 B. 3 C. 4 D. 5
【解析】通过观察未知数的系数,可采取两个方程相加得,5x+5y+5z = 25,所以 x+y+z = 5.
D
3. 在等式 y = ax2+bx+c 中,当 x = -1时,y = 0;当 x = 2 时,y = 3;当 x = 5 时,y = 60. 求 a,b,c 的值.
解:根据题意,得三元一次方程组:
②-①, 得 a+b =1 ④
③-①,得 4a+b = 10 ⑤
④ 与 ⑤ 组成二元一次方程组
解这个方程组,得
把 代入①,得
a = 3,
b = -2
c = -5
因此
a-b+c= 0, ①
4a+2b+c=3, ②
25a+5b+c=60. ③
a = 3,
b = -2.
a = 3,
b = -2,
c = -5.
a+b = 1,
4a+b = 10.
1. 解三元一次方程组的基本思路是什么?
消元,转化
三元一次方程组
二元一次方程组
转化
一元一次方程
转化
2. 在三元化二元时,对于具体方法的选取应该注意什么?
求解三元一次方程组:
观察
消元
代入消元
加减消元
力求简便
课堂小结
7.3 三元一次方程组的解法
七年级下
华师版
1. 了解三元一次方程组的概念,会解三元一次方程组,体会消元的思路,提高分析能力,计算能力.
2. 经过探索三元一次方程组的解法的过程,理解代入消元法和加减消元法所体现的化未知为已知的化归的思想方法.
学习目标
重点
难点
小明、小兰、小红三个人的年龄的和是 26 岁,小明比小兰大 1 岁,小明年龄的两倍与小红的年龄之和比小兰大 18 岁.
如何求三个小动物的年龄?
新课引入
根据题意,设小明、小兰、小红的年龄分别为 x岁、y岁、z岁, 可以列出以下三个方程:
x + y + z = 26,
x – y = 1,
2x + z – y = 18.
那么这三个方程的组合我们该如何称呼?又该如何去解未知数的值呢?这就是我们本节课要学习的内容.
在前面的课程中,我们应用二元一次方程组,求出了勇士队在“我们的小世界杯”足球赛第一轮比赛中胜与平的场数.
在第二轮比赛中,勇士队参加了 10 场比赛,按同样的计分规则,共得 18 分,已知勇士队在比赛中胜的场数正好等于平与负的场数之和,那么勇士队在第二轮比赛中,胜、负、平的场数各是多少?
新知学习
分析:问题中有三个未知数,如果设勇士队胜了 x 场,平了 y 场,负了 z 场,请你填写下表:
胜 平 负 合计
每场得分
场数
总得分
3
1
0
x
y
z
3x
y
0
10
18
根据一共 10 场比赛,得分 18 分,胜的场数等于平与负的场数之和,可列方程组为:
思考
1. 类比二元一次方程,上述方程组中每个方程都是 __________ 方程.
2. 上面的方程组应该叫做 __________ 方程组.
一次
三元一次
解:方程组
把 ③ 代入 ①②,整理得
解得
将其代入③得 x = 5.
所以
思考
上面的三元一次方程组能否用加减消元法求解?或者能否利用方程 ③,直接消去方程 ① 中的 y + z?比较一下,哪种方法更简便?
① + ③ 得,x + y + z + x = 10 + y + z
即 2x = 10
解得 x = 5.
例1 解方程:
解:由 ② 得 z = 7 - 3x + 2y ④,
把 ④ 代入 ① 和 ③,得
整理,得
解得
代入④,得 z = 7 - 3 - 6 = -2.
所以原方程组的解是
归纳
这里,我们用的是代入消元法:先由方程 ②,用含有 x、y 的代数式表示 z,再分别代入方程 ① 和方程 ③,消去未知数 z,转化为只含有 x、y 的二元一次方程组求解.
例2 解方程:
解:由③ - ②,得 3x + 6z = -24,即 x + 2z = -8.
①×3 + ②×4,得 17x - 17z = 17,即 x - z = 1.
得方程组 ,
解得
代入②,得 y = 0.
所以原方程的解为
归纳
上述例 1 和例 2 的解答分别应用了代入消元法和加减消元法,先消去某一个未知数,将三元一次方程组转化为二元一次方程组,然后解所得的方程组,得到 2 个未知数的值,进而求出第三个未知数的值,从而得到方程的解.
例3 解方程组
x + y + z = 2 ①
x – y + z = 0 ②
x – z = 4 ③
分析:1. 化“三元”为“二元”
考虑消去哪个未知数 ( 也就是三个未知数要去掉哪一个?)
解法一:消去 y,① + ② 得
x + z = 1 ④
联立 ③ 得
x – z = 4 ③
x + z = 1 ④
x + y + z = 2 ①
x – y + z = 0 ②
x – z = 4 ③
解法二:消去 x, 由 ③ 得 x = z + 4 ④
把 ④ 代入 ①、② 得,
(z + 4) + y + z = 2 ⑤
(z + 4) - y + z = 0 ⑥
化简得,
2z + y = -2, ⑦
2z - y = -4. ⑧
x + y + z = 2 ①
x – y + z = 0 ②
x – z = 4 ③
解法三:消去 z,由 ③ 得,z = x - 4 ④
把 ④ 代入 ①、② 得
x + y + (x - 4) = 2, ⑤
x - y + (x - 4) = 0. ⑥
化简得,
2x + y = 6, ⑦
2x - y = 4. ⑧
x + y + z = 2 ①
x – y + z = 0 ②
x – z = 4 ③
解:① + ② 得
x + z = 1 ④
联立 ③ 得
x – z = 4 ③
x + z = 1 ④
③ + ④,得 2x = 5
所以,原方程的解是
x =
y = 1
z =
例4 解方程组
x + y = 3 ①
y + z = 5 ②
z + x = 4 ③
解:③ - ②,得 x - y = -1 ④
① + ④,得 2x = 2
∴x = 1.
把 x = 1 代入方程 ①、③,分别得
y = 2,z = 3
x = 1,
所以,原方程组的解是 y = 2,
z = 3 .
例4 解方程组
x + y = 3 ①
y + z = 5 ②
z + x = 4 ③
例4 也可以这样解:
① + ② + ③ 得 2(x + y + z ) = 12 ④
即,x + y + z = 6 ⑤
⑤ - ①,得 z = 3
⑤ - ②,得 x = 1
⑤ - ③,得 y = 2
所以,原方程组的解是 x = 1,
y = 2,
z = 3 .
1. 解三元一次方程组的基本思路是什么?
消元,转化
三元一次方程组
二元一次方程组
转化
一元一次方程
转化
2. 在三元化二元时,对于具体方法的选取应该注意什么?
求解三元一次方程组:
观察
消元
代入消元
加减消元
力求简便
归纳
x + y + z = 12 ①
x + 2y + 5z = 22 ②
x = 4y ③
1. 解方程组
解:将 x = 4y 代入 ①、②.
4y + y + z = 12 ④
4y + 2y + 5z = 22 ⑤
化简得:
5y + z = 12 ⑥
6y + 5z = 22 ⑦
⑥×5 - ⑦,得 19y = 38
即 y = 2.
所以,原方程的解是
x = 8
y = 2
z = 2
随堂练习
2. 若 x+2y+3z = 10,4x+3y+2z = 15,则 x+y+z 的值为( )
A. 2 B. 3 C. 4 D. 5
【解析】通过观察未知数的系数,可采取两个方程相加得,5x+5y+5z = 25,所以 x+y+z = 5.
D
3. 在等式 y = ax2+bx+c 中,当 x = -1时,y = 0;当 x = 2 时,y = 3;当 x = 5 时,y = 60. 求 a,b,c 的值.
解:根据题意,得三元一次方程组:
②-①, 得 a+b =1 ④
③-①,得 4a+b = 10 ⑤
④ 与 ⑤ 组成二元一次方程组
解这个方程组,得
把 代入①,得
a = 3,
b = -2
c = -5
因此
a-b+c= 0, ①
4a+2b+c=3, ②
25a+5b+c=60. ③
a = 3,
b = -2.
a = 3,
b = -2,
c = -5.
a+b = 1,
4a+b = 10.
1. 解三元一次方程组的基本思路是什么?
消元,转化
三元一次方程组
二元一次方程组
转化
一元一次方程
转化
2. 在三元化二元时,对于具体方法的选取应该注意什么?
求解三元一次方程组:
观察
消元
代入消元
加减消元
力求简便
课堂小结
