7.4实践与探索 课件(共16张PPT)
文档属性
| 名称 | 7.4实践与探索 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 862.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
7.4 实践与探索
七年级下
华师版
1. 通过思考、讨论、探索事物之间的数量关系,形成方程模型.
2. 通过自主探索,相互交流,尝试用二元一次方程组解决与生活密切相关的问题.
学习目标
重点
难点
周日小明家里来了一些客人,用餐时从厨房拿碗筷的任务落在小明身上,若已知他所要拿的碗的个数和筷子的根数加起来恰好是 24,且已知每人需配一个碗和两根筷子. 讨论一下,他拿了多少个碗和多少根筷子?
解:设他拿了 x 个碗和 y 根筷子.
可得方程 ,
解方程,得 .
答:他拿了 8 个碗,16 根筷子.
新课引入
问题1:要用 20 张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,一部分做底面. 已知每张白卡纸可以做 2 个侧面,或者做 3 个底面. 如果 1 个侧面和 2 个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?
分析:1. 本题有哪些已知量?
(1) 20 张白卡纸;(2) 一张白卡纸可以做 2 个侧面,或者做 3 个底面;
(3) 如果 1 个侧面和 2 个底面可以做成一个包装盒.
新知学习
2. 若设用 x 张白卡纸做盒身,y 张白卡纸做盒底.
那么可以做盒身 _____ 个,盒底 _____ 个.
(1) 做盒身的白卡纸 + 做盒底的白卡纸 = 20;
(2) 2×盒身数量 = 盒底数量.
2x
3y
3. 题中的等量关系有哪些?
根据题意,得
解得
对这个结果进行分析,你发现了什么?
4. 如果仅对结果进行分析,发现能做 _____ 套包装盒,此时还多 _____ 张白卡纸.
16
1
5. 如果可以将一张白卡纸裁出一个侧面和一个底面,该如何分这些白卡纸,才能即使作出的侧面和底面配套,又能充分利用白卡纸?
解:用 _____ 张白卡纸做盒身,可做 _____ 个;用 _____ 张白卡纸做盒底,可做 _____ 个. 将余下的 1 张白卡纸剪成两半, 一半做1个盒身,一半做1个盒底,一共可做 _____ 个包装盒,较充分地利用了材料.
8
16
11
33
17
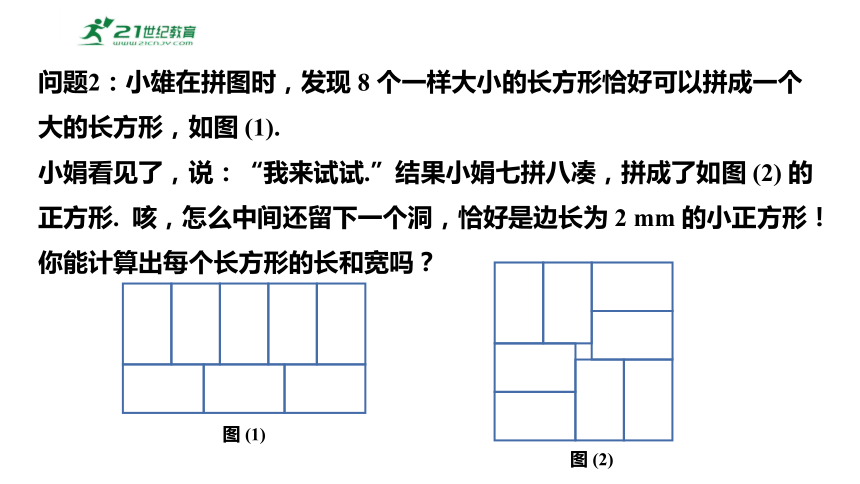
问题2:小雄在拼图时,发现 8 个一样大小的长方形恰好可以拼成一个大的长方形,如图 (1).
小娟看见了,说:“我来试试.”结果小娟七拼八凑,拼成了如图 (2) 的正方形. 咳,怎么中间还留下一个洞,恰好是边长为 2 mm 的小正方形!你能计算出每个长方形的长和宽吗?
图 (1)
图 (2)
分析:设每个小长方形的长为 x mm,宽为 y mm.
图2给我们提供了一个信息:
S大正方形 - 8×S长方形 = 22,
即 (x + 2y)2 - 8xy = 4.
根据这个式子你能求出长化和宽吗?
根据上面的式子显然不能求出长和宽.
图 (2)
图 (1)
图 (2)
根据图形给出的信息,
(1) 长方形的 _____ 个宽与其 _____ 个长相等;
(2) 两个长加 2 的和等于 _____ 个长与 _____ 个宽的和.
5
3
1
2
根据题意可得方程组
解得
答:小长方形的长为 10 mm,宽为 6 mm.
1. 下面是小娟到商店购买 2 个单价相同的布丁和 10 根单价相同的棒棒糖的经过.
小娟:我要 2 个布丁和 10 根棒棒糖.
老板:好的!这是您要的 2 个布丁和 10 根棒棒糖,总共 20 元!
老板:小朋友,我算错了,我多算了 2 根棒棒糖的钱,退还你 2 元.
根据上文,判断布丁和棒棒糖的单价相差 ( )
A. 2 元 B. 3 元 C. 4 元 D. 5 元
B
随堂练习
2.《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱 48 文;如果乙得到甲所有钱的 ,那么乙也共有钱 48 文,甲、乙两人原来各有多少钱?设甲原有 x 文钱,乙原有 y 文钱,可列方程组是
___________
3.“中国结”是临沂市红花镇的传统手工艺产业,该镇某工厂有54名工人,一名工人一天可制作300条流苏或75个结体.若一款中国结由一个结体佩戴两条流苏构成,则应怎样安排人力才能使每天制作的这款中国结刚好完整?
4. 根据图中的信息,求梅花鹿和长颈鹿现在的高度.
解:设梅花鹿的高度是 x m,长颈鹿的高度是 y m,
根据题意得
解得
答:梅花鹿的高度是 1.5 m,长颈鹿的高度是 5.5 m.
5. 被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为 342 km,隧道累计长度的 2 倍比桥梁累计长度多 36 km. 求隧道累计长度与桥梁累计长度.
解:设隧道累计长度为 x km,桥梁累计长度为 y km,
根据题意得
解得
答:隧道累计长度为 126 km,桥梁累计长度为 216 km.
6.小元爸爸在家附近的新能源汽车公共充电桩给汽车充电,第一次充电5小时,共花费14元;第二次充电7小时,共花费18元,充电费用标准如下表,则a的值为____,b的值为____.
充电时长(小时) 电费(元/小时)
4小时及以内 a
超过4小时的部分 b
3
2
在用二元一次方程组解决实际问题时,你会怎样设定未知数,可借助哪些方式辅助分析问题中的相等关系?
设未知数的方式一般有两种,分别是直接设元与间接设元.
当问题较为复杂的时候,有时设与要求的未知量相关的另一些量为未知数,即间接设元.
课堂小结
7.4 实践与探索
七年级下
华师版
1. 通过思考、讨论、探索事物之间的数量关系,形成方程模型.
2. 通过自主探索,相互交流,尝试用二元一次方程组解决与生活密切相关的问题.
学习目标
重点
难点
周日小明家里来了一些客人,用餐时从厨房拿碗筷的任务落在小明身上,若已知他所要拿的碗的个数和筷子的根数加起来恰好是 24,且已知每人需配一个碗和两根筷子. 讨论一下,他拿了多少个碗和多少根筷子?
解:设他拿了 x 个碗和 y 根筷子.
可得方程 ,
解方程,得 .
答:他拿了 8 个碗,16 根筷子.
新课引入
问题1:要用 20 张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,一部分做底面. 已知每张白卡纸可以做 2 个侧面,或者做 3 个底面. 如果 1 个侧面和 2 个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?
分析:1. 本题有哪些已知量?
(1) 20 张白卡纸;(2) 一张白卡纸可以做 2 个侧面,或者做 3 个底面;
(3) 如果 1 个侧面和 2 个底面可以做成一个包装盒.
新知学习
2. 若设用 x 张白卡纸做盒身,y 张白卡纸做盒底.
那么可以做盒身 _____ 个,盒底 _____ 个.
(1) 做盒身的白卡纸 + 做盒底的白卡纸 = 20;
(2) 2×盒身数量 = 盒底数量.
2x
3y
3. 题中的等量关系有哪些?
根据题意,得
解得
对这个结果进行分析,你发现了什么?
4. 如果仅对结果进行分析,发现能做 _____ 套包装盒,此时还多 _____ 张白卡纸.
16
1
5. 如果可以将一张白卡纸裁出一个侧面和一个底面,该如何分这些白卡纸,才能即使作出的侧面和底面配套,又能充分利用白卡纸?
解:用 _____ 张白卡纸做盒身,可做 _____ 个;用 _____ 张白卡纸做盒底,可做 _____ 个. 将余下的 1 张白卡纸剪成两半, 一半做1个盒身,一半做1个盒底,一共可做 _____ 个包装盒,较充分地利用了材料.
8
16
11
33
17
问题2:小雄在拼图时,发现 8 个一样大小的长方形恰好可以拼成一个大的长方形,如图 (1).
小娟看见了,说:“我来试试.”结果小娟七拼八凑,拼成了如图 (2) 的正方形. 咳,怎么中间还留下一个洞,恰好是边长为 2 mm 的小正方形!你能计算出每个长方形的长和宽吗?
图 (1)
图 (2)
分析:设每个小长方形的长为 x mm,宽为 y mm.
图2给我们提供了一个信息:
S大正方形 - 8×S长方形 = 22,
即 (x + 2y)2 - 8xy = 4.
根据这个式子你能求出长化和宽吗?
根据上面的式子显然不能求出长和宽.
图 (2)
图 (1)
图 (2)
根据图形给出的信息,
(1) 长方形的 _____ 个宽与其 _____ 个长相等;
(2) 两个长加 2 的和等于 _____ 个长与 _____ 个宽的和.
5
3
1
2
根据题意可得方程组
解得
答:小长方形的长为 10 mm,宽为 6 mm.
1. 下面是小娟到商店购买 2 个单价相同的布丁和 10 根单价相同的棒棒糖的经过.
小娟:我要 2 个布丁和 10 根棒棒糖.
老板:好的!这是您要的 2 个布丁和 10 根棒棒糖,总共 20 元!
老板:小朋友,我算错了,我多算了 2 根棒棒糖的钱,退还你 2 元.
根据上文,判断布丁和棒棒糖的单价相差 ( )
A. 2 元 B. 3 元 C. 4 元 D. 5 元
B
随堂练习
2.《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱 48 文;如果乙得到甲所有钱的 ,那么乙也共有钱 48 文,甲、乙两人原来各有多少钱?设甲原有 x 文钱,乙原有 y 文钱,可列方程组是
___________
3.“中国结”是临沂市红花镇的传统手工艺产业,该镇某工厂有54名工人,一名工人一天可制作300条流苏或75个结体.若一款中国结由一个结体佩戴两条流苏构成,则应怎样安排人力才能使每天制作的这款中国结刚好完整?
4. 根据图中的信息,求梅花鹿和长颈鹿现在的高度.
解:设梅花鹿的高度是 x m,长颈鹿的高度是 y m,
根据题意得
解得
答:梅花鹿的高度是 1.5 m,长颈鹿的高度是 5.5 m.
5. 被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为 342 km,隧道累计长度的 2 倍比桥梁累计长度多 36 km. 求隧道累计长度与桥梁累计长度.
解:设隧道累计长度为 x km,桥梁累计长度为 y km,
根据题意得
解得
答:隧道累计长度为 126 km,桥梁累计长度为 216 km.
6.小元爸爸在家附近的新能源汽车公共充电桩给汽车充电,第一次充电5小时,共花费14元;第二次充电7小时,共花费18元,充电费用标准如下表,则a的值为____,b的值为____.
充电时长(小时) 电费(元/小时)
4小时及以内 a
超过4小时的部分 b
3
2
在用二元一次方程组解决实际问题时,你会怎样设定未知数,可借助哪些方式辅助分析问题中的相等关系?
设未知数的方式一般有两种,分别是直接设元与间接设元.
当问题较为复杂的时候,有时设与要求的未知量相关的另一些量为未知数,即间接设元.
课堂小结
