9.3用正多边形铺设地面 课件(共25张PPT)
文档属性
| 名称 | 9.3用正多边形铺设地面 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 16:21:41 | ||
图片预览


文档简介
(共25张PPT)
9.3 用正多边形铺设地面
七年级下
华师版
1. 理解用相同的正多边形铺设地面的理论依据,会用相同正多边形进行平面镶嵌.
2. 知道怎样的正多边形能无空隙的铺设地面.
3. 知道哪几种正多边形能组合在一起铺满地面.
学习目标
重点
难点
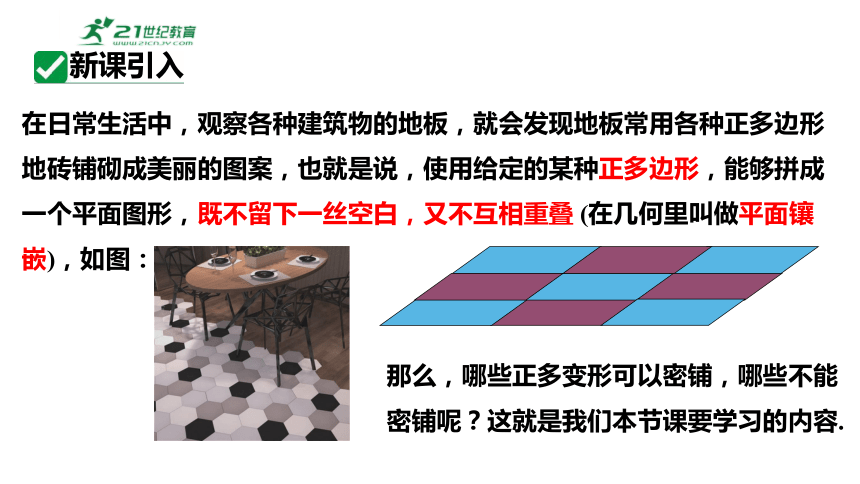
在日常生活中,观察各种建筑物的地板,就会发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某种正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠 (在几何里叫做平面镶嵌),如图:
新课引入
那么,哪些正多变形可以密铺,哪些不能密铺呢?这就是我们本节课要学习的内容.
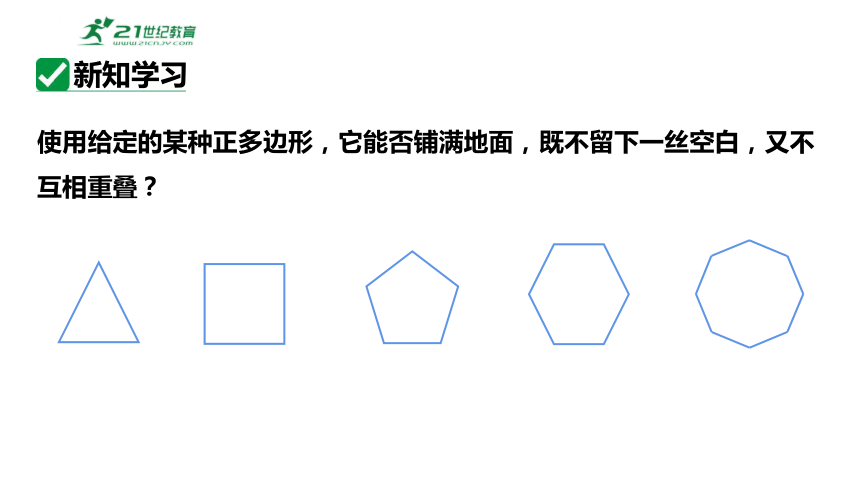
使用给定的某种正多边形,它能否铺满地面,既不留下一丝空白,又不互相重叠?
新知学习
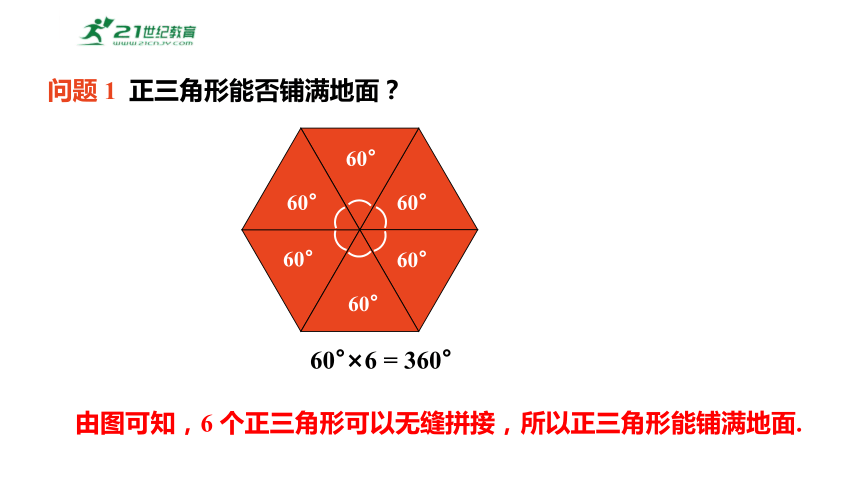
问题 1 正三角形能否铺满地面?
由图可知,6 个正三角形可以无缝拼接,所以正三角形能铺满地面.
60°×6 = 360°
60°
60°
60°
60°
60°
60°
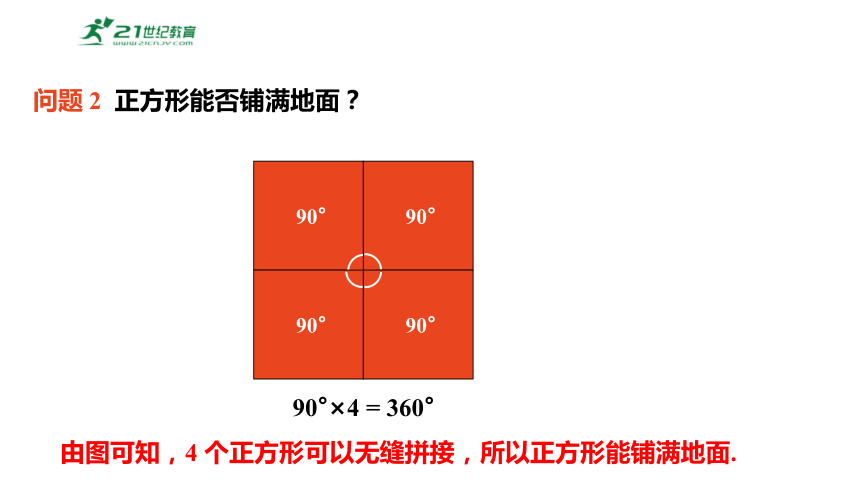
问题 2 正方形能否铺满地面?
由图可知,4 个正方形可以无缝拼接,所以正方形能铺满地面.
90°
90°
90°
90°
90°×4 = 360°
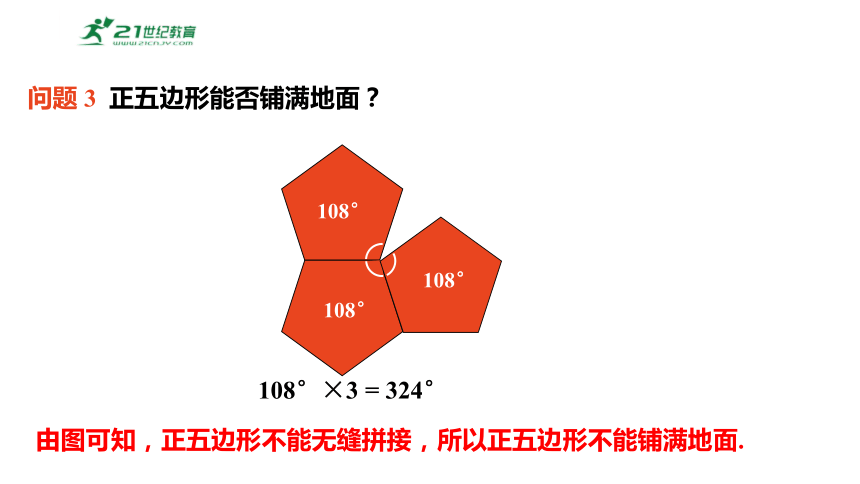
问题 3 正五边形能否铺满地面?
由图可知,正五边形不能无缝拼接,所以正五边形不能铺满地面.
108°
108°
108°
108°×3 = 324°
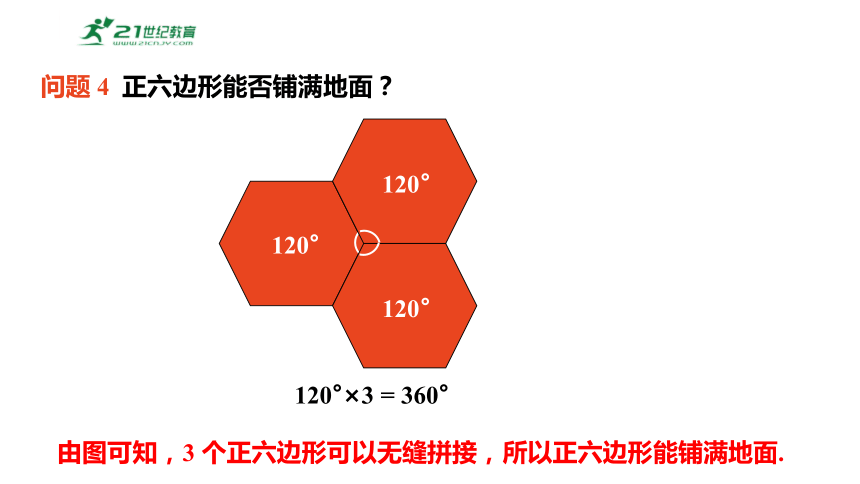
问题 4 正六边形能否铺满地面?
由图可知,3 个正六边形可以无缝拼接,所以正六边形能铺满地面.
120°
120°
120°
120°×3 = 360°
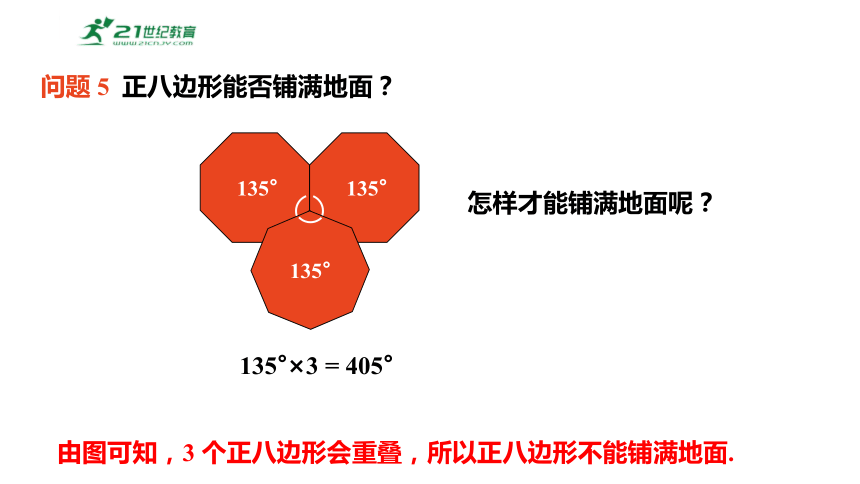
问题 5 正八边形能否铺满地面?
由图可知,3 个正八边形会重叠,所以正八边形不能铺满地面.
135°
135°
135°
135°×3 = 405°
怎样才能铺满地面呢?
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
归纳
一个内角度数 能否铺满平面 图形 一个顶点周围正多形个数
正三角形
正方形
正五边形
正六边形
6
4
3
能
能
能
不能
90°
108°
60°
120°
问题 5 还能找到其他正多边形铺满地面吗?
分析:要用相同正多边形铺满地面的关键是看,这种正多边形的一个内角的倍数是否是360°,在正多边形里,只有正三角形、正四边形、正六边形这三种正多边形满足条件.所以,在正多边形里,用相同正多边形铺满地面的只有正三角形、正四边形、正六边形,而其他的正多边形不可以.
用相同正多边形可以铺满地面的条件:
正多边形的每个内角都能被 360°整除.
归纳
例1 铺设一间长 6 m、宽 3.5 m 的客厅地面需要同样规格的正方形地板砖,现有“40 cm×40 cm”“30 cm×30 cm”“50 cm×50 cm”和“60 cm×60 cm”的地板砖,请你设计一下,要想全部铺满,不锯破且不留一点空隙,选哪一种规格?为什么?需要多少块?
解:选“50 cm×50 cm”规格的.
理由:∵6 m =600c m,3.5 m = 350 cm,
600,350 都是 50 的倍数,
∴选“50 cm×5 0cm”规格的.
需要 7×12 = 84(块).
例2 某学校想用地砖铺地面,学校已准备了一批完全相同的正 n 边形 [n 为 (1) 中的所求值],如果单独用这种地砖,能密铺吗?
(3) 如果不能,请你自己只选用一种同 (2) 边长相同的正方形地砖搭配,能密铺吗?如果能,请你画出一片密铺的示意图.
(2) 正八边形的每个内角为 135°,不能整除 360°,所以不能密铺.
(3) 边长相同的正方形地砖搭配能密铺.
思考
问题6 从正三角形、正方形、正五边形、正六边形中任取两种或三种进行组合是否能铺满地面呢?
正方形、正三角形
正六边形、正三角形
正六边形、正方形、正三角形
归纳
多种正多边形应该满足什么样的条件才能铺满地面?
围绕一点拼在一起的多种正多边形的内角之和为 360 .
关键:
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面.如:正五边形与正十边形的组合.
模型:
正多边形 1 的个数×正多边形 1 的内角度数 +
正多边形 2 的个数×正多边形 2 的内角度数 +… = 360
例3 你能说说用正方形和正六边形不能镶嵌成一个平面图案的原因吗?
解:正方形的一个内角为 90°,正六边形的一个内角为 120°,
设若能进行平面镶嵌时正方形有 x 个,正六边形有 y 个,
则 90x + 120y = 360,
此时方程 x、y 都是正整数,找不到同时满足 x、y 均为正整数的解,
故正方形和正六边形不能平面镶嵌.
1. 用一种正多边形可以进行平面铺设的条件是 ( )
A. 每个内角的度数都是整数
B. 每个内角的度数能整除 180°
C. 每个内角的度数能整除 360°
D. 边数是 3 的倍数
C
随堂练习
2. 若用规格相同的正六边形地砖铺地面,则围绕在一个顶点处的地砖的块数为 ( )
A. 3 B. 4 C. 5 D. 6
A
3. 在下列正多边形组合中,不能铺满地面的是( )
A. 正八边形和正方形 B. 正五边形和正八边形
C. 正六边形和正三角形 D. 正三角形和正方形
B
4. 一幅美丽的图案,在某个顶点处由四个边长相等的正多边形铺满,其中的三个分别为正三角形、正方形、正六边形,那么另外一个为( )
A. 正三角形 B. 正方形
C. 正五边形 D. 正六边形
B
5. 利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有 a 块正三角形和 b 块正六边形的地砖 (ab ≠ 0),则 a + b 的值为
( )
A. 3 或 4 B. 4 或 5
C. 5 或 6 D. 4
B
6. 用黑白两种颜色的正六边形地砖按如图所示的规律拼成若干图案,则n = 8 时,白色地砖共有 ______ 块.
34
7. 如图 ① 是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2 的正方形图案 (如图 ②),其中完整的圆共有 5 个,如果铺成一个3×3 的正方形图案 (如图 ③),其中完整的圆共有 13 个,如果铺成一个4×4 的正方形图案 (如图 ④),其中完整的圆共有 25 个,若这样铺成一个 10×10 的正方形图案,则其中完整的圆共有 _____ 个.
181
1. 某种正多边形密铺地面的条件是什么?
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
2. 单独用哪种正多边形可以铺满地面?
正三角形、正方形、正六边形
课堂小结
多种正多边形应该满足什么样的条件才能铺满地面?
围绕一点拼在一起的多种正多边形的内角之和为 360 .
关键:
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面.如:正五边形与正十边形的组合.
模型:
正多边形 1 的个数×正多边形 1 的内角度数 +
正多边形 2 的个数×正多边形 2 的内角度数 +… = 360
9.3 用正多边形铺设地面
七年级下
华师版
1. 理解用相同的正多边形铺设地面的理论依据,会用相同正多边形进行平面镶嵌.
2. 知道怎样的正多边形能无空隙的铺设地面.
3. 知道哪几种正多边形能组合在一起铺满地面.
学习目标
重点
难点
在日常生活中,观察各种建筑物的地板,就会发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某种正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠 (在几何里叫做平面镶嵌),如图:
新课引入
那么,哪些正多变形可以密铺,哪些不能密铺呢?这就是我们本节课要学习的内容.
使用给定的某种正多边形,它能否铺满地面,既不留下一丝空白,又不互相重叠?
新知学习
问题 1 正三角形能否铺满地面?
由图可知,6 个正三角形可以无缝拼接,所以正三角形能铺满地面.
60°×6 = 360°
60°
60°
60°
60°
60°
60°
问题 2 正方形能否铺满地面?
由图可知,4 个正方形可以无缝拼接,所以正方形能铺满地面.
90°
90°
90°
90°
90°×4 = 360°
问题 3 正五边形能否铺满地面?
由图可知,正五边形不能无缝拼接,所以正五边形不能铺满地面.
108°
108°
108°
108°×3 = 324°
问题 4 正六边形能否铺满地面?
由图可知,3 个正六边形可以无缝拼接,所以正六边形能铺满地面.
120°
120°
120°
120°×3 = 360°
问题 5 正八边形能否铺满地面?
由图可知,3 个正八边形会重叠,所以正八边形不能铺满地面.
135°
135°
135°
135°×3 = 405°
怎样才能铺满地面呢?
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
归纳
一个内角度数 能否铺满平面 图形 一个顶点周围正多形个数
正三角形
正方形
正五边形
正六边形
6
4
3
能
能
能
不能
90°
108°
60°
120°
问题 5 还能找到其他正多边形铺满地面吗?
分析:要用相同正多边形铺满地面的关键是看,这种正多边形的一个内角的倍数是否是360°,在正多边形里,只有正三角形、正四边形、正六边形这三种正多边形满足条件.所以,在正多边形里,用相同正多边形铺满地面的只有正三角形、正四边形、正六边形,而其他的正多边形不可以.
用相同正多边形可以铺满地面的条件:
正多边形的每个内角都能被 360°整除.
归纳
例1 铺设一间长 6 m、宽 3.5 m 的客厅地面需要同样规格的正方形地板砖,现有“40 cm×40 cm”“30 cm×30 cm”“50 cm×50 cm”和“60 cm×60 cm”的地板砖,请你设计一下,要想全部铺满,不锯破且不留一点空隙,选哪一种规格?为什么?需要多少块?
解:选“50 cm×50 cm”规格的.
理由:∵6 m =600c m,3.5 m = 350 cm,
600,350 都是 50 的倍数,
∴选“50 cm×5 0cm”规格的.
需要 7×12 = 84(块).
例2 某学校想用地砖铺地面,学校已准备了一批完全相同的正 n 边形 [n 为 (1) 中的所求值],如果单独用这种地砖,能密铺吗?
(3) 如果不能,请你自己只选用一种同 (2) 边长相同的正方形地砖搭配,能密铺吗?如果能,请你画出一片密铺的示意图.
(2) 正八边形的每个内角为 135°,不能整除 360°,所以不能密铺.
(3) 边长相同的正方形地砖搭配能密铺.
思考
问题6 从正三角形、正方形、正五边形、正六边形中任取两种或三种进行组合是否能铺满地面呢?
正方形、正三角形
正六边形、正三角形
正六边形、正方形、正三角形
归纳
多种正多边形应该满足什么样的条件才能铺满地面?
围绕一点拼在一起的多种正多边形的内角之和为 360 .
关键:
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面.如:正五边形与正十边形的组合.
模型:
正多边形 1 的个数×正多边形 1 的内角度数 +
正多边形 2 的个数×正多边形 2 的内角度数 +… = 360
例3 你能说说用正方形和正六边形不能镶嵌成一个平面图案的原因吗?
解:正方形的一个内角为 90°,正六边形的一个内角为 120°,
设若能进行平面镶嵌时正方形有 x 个,正六边形有 y 个,
则 90x + 120y = 360,
此时方程 x、y 都是正整数,找不到同时满足 x、y 均为正整数的解,
故正方形和正六边形不能平面镶嵌.
1. 用一种正多边形可以进行平面铺设的条件是 ( )
A. 每个内角的度数都是整数
B. 每个内角的度数能整除 180°
C. 每个内角的度数能整除 360°
D. 边数是 3 的倍数
C
随堂练习
2. 若用规格相同的正六边形地砖铺地面,则围绕在一个顶点处的地砖的块数为 ( )
A. 3 B. 4 C. 5 D. 6
A
3. 在下列正多边形组合中,不能铺满地面的是( )
A. 正八边形和正方形 B. 正五边形和正八边形
C. 正六边形和正三角形 D. 正三角形和正方形
B
4. 一幅美丽的图案,在某个顶点处由四个边长相等的正多边形铺满,其中的三个分别为正三角形、正方形、正六边形,那么另外一个为( )
A. 正三角形 B. 正方形
C. 正五边形 D. 正六边形
B
5. 利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有 a 块正三角形和 b 块正六边形的地砖 (ab ≠ 0),则 a + b 的值为
( )
A. 3 或 4 B. 4 或 5
C. 5 或 6 D. 4
B
6. 用黑白两种颜色的正六边形地砖按如图所示的规律拼成若干图案,则n = 8 时,白色地砖共有 ______ 块.
34
7. 如图 ① 是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2 的正方形图案 (如图 ②),其中完整的圆共有 5 个,如果铺成一个3×3 的正方形图案 (如图 ③),其中完整的圆共有 13 个,如果铺成一个4×4 的正方形图案 (如图 ④),其中完整的圆共有 25 个,若这样铺成一个 10×10 的正方形图案,则其中完整的圆共有 _____ 个.
181
1. 某种正多边形密铺地面的条件是什么?
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
2. 单独用哪种正多边形可以铺满地面?
正三角形、正方形、正六边形
课堂小结
多种正多边形应该满足什么样的条件才能铺满地面?
围绕一点拼在一起的多种正多边形的内角之和为 360 .
关键:
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面.如:正五边形与正十边形的组合.
模型:
正多边形 1 的个数×正多边形 1 的内角度数 +
正多边形 2 的个数×正多边形 2 的内角度数 +… = 360
