10.1.1生活中的轴对称 课件(共19张PPT)
文档属性
| 名称 | 10.1.1生活中的轴对称 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
10.1.1 生活中的轴对称
七年级下
华师版
1. 通过欣赏、折叠等活动,认识轴对称图形的共同特征,能识别简单的轴对称图形及对称轴.
2. 通过实践操作,理解轴对称图形和两个图形成轴对称的区别.
3. 判别一个图形是否是轴对称图形,轴对称图形与两个图形成轴对称的区别与联系.
难点
重点
学习目标
新课引入
欣赏生活中的图片:
1. 这些美丽的图形来自生活,把这些图形沿着某条直线对折一下,看看对折后的两部分能完全重合吗?如果折一次得不到你想要的结果,那在多折几次试试.
探究
生活中有很多类似的现象,如从镜子里看到自己的像,把手掌盖在镜子上,镜子里的手与自己的手完全重合在一起,这些都可以称为对称,你还能举些例子吗?
那么,什么是对称?对称的特点是什么?这就是本节课所要学习的内容.
新知学习
轴对称图形的概念:
归纳
如果一个图形沿着某条直线对折后,对折的两部分是完全重合的,那么这个图形就是轴对称图形,这条直线就叫做这个图形的对称轴.
轴对称图形
对称轴
1. “完全重合”的意思是 __________.
思考
完全相等
2. 这条直线可以不经过这个图形本身吗?
不可以.
3. 圆的直径是圆的对称轴吗?
不是.直径所在的直线是圆的对称轴.
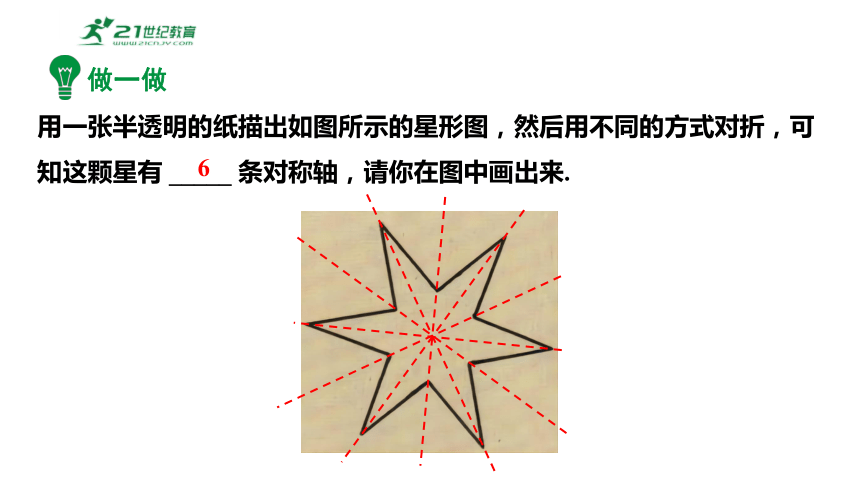
用一张半透明的纸描出如图所示的星形图,然后用不同的方式对折,可知这颗星有 _____ 条对称轴,请你在图中画出来.
6
做一做
温馨提示
(1) 对称轴是一条直线,而不是线段或射线.
(2) 一个轴对称图形的对称轴可以有一条,也可以有两条,还可以有无数条,要视图形具体分析判定.
例1 找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
...
探究
2. 观察图形,形成概念.
我们再看两组图形.
想一想,每组图形中,左边图形沿虚线对折后与右边图形有怎样的关系?
左边图形沿虚线对折后与右边图形完全重合.
归纳
上面每组图形中的两个图形关于虚线成轴对称,你能对比轴对称图形的概念,试着总结一下什么叫做两个图形成轴对称吗?
把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点 (即两个图形重合时互相重合的点) 叫做对称点.
轴对称图形与两个图形成轴对称的区别与联系:
轴对称图形 两个图形成轴对称
图形
区别
联系 有特殊位置关系的两个相同图形
1. 都是沿着某条直线折叠后能重合;
2. 可以通过分割或整合互相转化.
具有特殊形状的一个图形
例2. 请你标出图中 A、B、C 三点的对称点 A1、B1、C1.
A1
B1
C1
例3. 在纸上滴几滴墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称?它的对称轴是什么呢?
是关于折痕对称,它的对称轴就是折痕
归纳
轴对称图形 (或成轴对称的两个图形) 沿对称轴对折后的两部分是完全重合的.
轴对称图形 (或成轴对称的两个图形) 的对称线段 (对折后重合的线段) 相等,对应角 (对折后能够重合的角) 相等.
随堂练习
1.下列图形中,一定是轴对称图形的是( )
A.锐角三角形 B.曲线
C.线段 D.直角三角形
C
2.如图,哪一个选项中的右边图形与左边图形成轴对称( )
A
B
C
D
C
3. 下列交通标志中哪些是轴对称图形?
×
√
×
√
课堂小结
轴对称
如果一个图形,把它沿某条直线折叠后,对折后的两部门能完全重合,即为轴对称图形,这条直线即为这个图形的对称轴
把一个图形沿着某一条直线翻折过去,如果能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,
定义
区别
轴对称图形:具有特殊形状的一个图形
成轴对称:有着特殊位置关系的两个相同图形
10.1.1 生活中的轴对称
七年级下
华师版
1. 通过欣赏、折叠等活动,认识轴对称图形的共同特征,能识别简单的轴对称图形及对称轴.
2. 通过实践操作,理解轴对称图形和两个图形成轴对称的区别.
3. 判别一个图形是否是轴对称图形,轴对称图形与两个图形成轴对称的区别与联系.
难点
重点
学习目标
新课引入
欣赏生活中的图片:
1. 这些美丽的图形来自生活,把这些图形沿着某条直线对折一下,看看对折后的两部分能完全重合吗?如果折一次得不到你想要的结果,那在多折几次试试.
探究
生活中有很多类似的现象,如从镜子里看到自己的像,把手掌盖在镜子上,镜子里的手与自己的手完全重合在一起,这些都可以称为对称,你还能举些例子吗?
那么,什么是对称?对称的特点是什么?这就是本节课所要学习的内容.
新知学习
轴对称图形的概念:
归纳
如果一个图形沿着某条直线对折后,对折的两部分是完全重合的,那么这个图形就是轴对称图形,这条直线就叫做这个图形的对称轴.
轴对称图形
对称轴
1. “完全重合”的意思是 __________.
思考
完全相等
2. 这条直线可以不经过这个图形本身吗?
不可以.
3. 圆的直径是圆的对称轴吗?
不是.直径所在的直线是圆的对称轴.
用一张半透明的纸描出如图所示的星形图,然后用不同的方式对折,可知这颗星有 _____ 条对称轴,请你在图中画出来.
6
做一做
温馨提示
(1) 对称轴是一条直线,而不是线段或射线.
(2) 一个轴对称图形的对称轴可以有一条,也可以有两条,还可以有无数条,要视图形具体分析判定.
例1 找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
...
探究
2. 观察图形,形成概念.
我们再看两组图形.
想一想,每组图形中,左边图形沿虚线对折后与右边图形有怎样的关系?
左边图形沿虚线对折后与右边图形完全重合.
归纳
上面每组图形中的两个图形关于虚线成轴对称,你能对比轴对称图形的概念,试着总结一下什么叫做两个图形成轴对称吗?
把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点 (即两个图形重合时互相重合的点) 叫做对称点.
轴对称图形与两个图形成轴对称的区别与联系:
轴对称图形 两个图形成轴对称
图形
区别
联系 有特殊位置关系的两个相同图形
1. 都是沿着某条直线折叠后能重合;
2. 可以通过分割或整合互相转化.
具有特殊形状的一个图形
例2. 请你标出图中 A、B、C 三点的对称点 A1、B1、C1.
A1
B1
C1
例3. 在纸上滴几滴墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称?它的对称轴是什么呢?
是关于折痕对称,它的对称轴就是折痕
归纳
轴对称图形 (或成轴对称的两个图形) 沿对称轴对折后的两部分是完全重合的.
轴对称图形 (或成轴对称的两个图形) 的对称线段 (对折后重合的线段) 相等,对应角 (对折后能够重合的角) 相等.
随堂练习
1.下列图形中,一定是轴对称图形的是( )
A.锐角三角形 B.曲线
C.线段 D.直角三角形
C
2.如图,哪一个选项中的右边图形与左边图形成轴对称( )
A
B
C
D
C
3. 下列交通标志中哪些是轴对称图形?
×
√
×
√
课堂小结
轴对称
如果一个图形,把它沿某条直线折叠后,对折后的两部门能完全重合,即为轴对称图形,这条直线即为这个图形的对称轴
把一个图形沿着某一条直线翻折过去,如果能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,
定义
区别
轴对称图形:具有特殊形状的一个图形
成轴对称:有着特殊位置关系的两个相同图形
