10.3.2旋转的特征 课件(共18张PPT)
文档属性
| 名称 | 10.3.2旋转的特征 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 16:21:41 | ||
图片预览






文档简介
(共18张PPT)
10.3.2 旋转的特征
七年级下
华师版
1. 通过具体实例进一步认识旋转,掌握旋转的特征.
2. 经历对具有旋转特征的图形进行观察、分析.
3.会利用旋转的特征解决图形问题.
学习目标
难点
重点
观察下面的图片,想一想它们与基本图形之间有什么关系?是经过怎样变换得到的?
新课引入
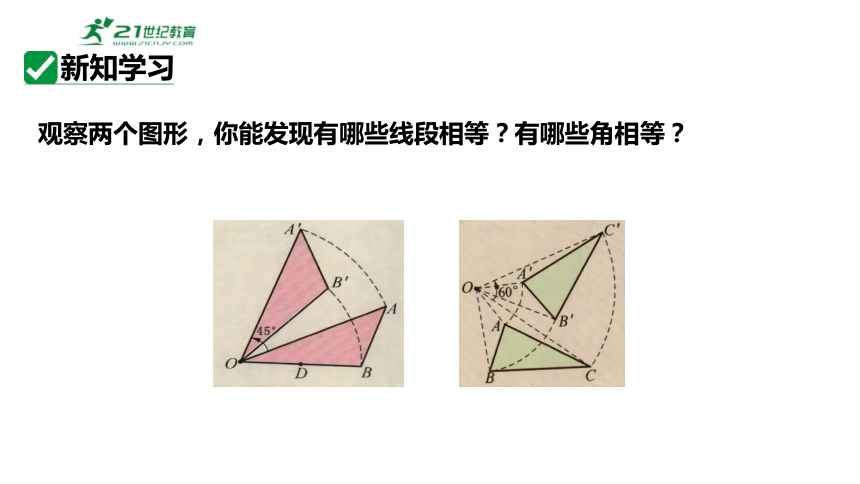
观察两个图形,你能发现有哪些线段相等?有哪些角相等?
新知学习
思考并完成填空:
(1) 中,线段 OA、OB 都是绕点 O 旋转 45° 角到对应线段 OA′ 与 OB′,而且 OA = _____,OB = _____,AB = _____;∠AOB = _______,∠A = _____,∠B = _____.
(2) 中,旋转中心是点 O,点 A、B、C 都是绕点 O 旋转 60° 角到对应点 A′、B′、C′,而且 OA = _____,OB = _____,OC = _____;AB = _____,BC = _____,CA = _____;∠CAB = ________,∠ABC = ________,∠BCA = ________.
OA′
OB′
A′B′
∠A′OB′
∠A′
∠B′
OA′
OB′
OC′
A′B′
B′C′
C′A′
∠C′A′B′
∠A′B′C′
∠B′C′A′
(1)
(2)
归纳
图形旋转的特征:
图形中每一个点都绕着旋转中心沿着同一方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小都没有发生变化.
温馨提示
(1) 旋转不改变图形的大小和形状,只改变图形的位置;
(2) 经过旋转,图形上的每一点都绕旋转中心沿相同的方向旋转了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等;
(3) 分析旋转形成的方法:“三个一”,即分析一个中心,一个方向,一个角度.
温馨提示
易错警示:
画旋转图形时容易忽视对旋转方向的要求,除了旋转中心及旋转角之外,还应指明旋转方向是顺时针还是逆时针,若无特别说明,则应考虑两种情况.
例 同学们曾玩过万花筒,它是由三块等长的玻璃片围成的. 如图是在万花筒中看到的一个图案. 图中所有小三角形是大小相同的等边三角形,其中的四边形 AEFG 可以看成是把四边形 ABCD 以 A 为旋转中心 ( )
A. 顺时针旋转 60° 得到 B. 顺时针旋转 120° 得到
C. 逆时针旋转 60° 得到 D. 逆时针旋转 120° 得到
B
分析:根据图形可知∠BAE = 120°,AB 边绕点 A 顺时针旋转 120° 得到 AE 边,所以四边形 AEFG 可以看成是把四边形 ABCD 以 A 为旋转中心顺时针旋转 120° 得到的.
确定旋转中心与旋转角的方法:
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是在图形外,若在图形上,哪一点在旋转过程中位置没有改变,这一点就是旋转中心;若在图形外,对应点连线的中垂线的交点就是旋转中心.旋转角就是对应线段的夹角或对应点与旋转中心连线的夹角.
归纳
1. 如图,△ODC 是由△OAB 绕点 O 顺时针旋转 30° 后得到的图形,若点 D 恰好落在 AB 上,且∠AOC 的度数为 100°,则∠DOB 的度数是
( )
A. 40° B. 30°
C. 38° D. 15°
A
随堂练习
2. 如图,将△AOB 绕点 O 按逆时针方向旋转 45° 后得到△COD,若∠AOB = 15°,则∠AOD 的度数是 _____.
60°
3. 如图所示,△ABC 是直角三角形,延长 AB 到 D,使 BD = BC,在 BC 上取 BE = AB,连结 DE. △ABC 顺时针旋转后能与△EBD 重合,那么
(1) 旋转中心是哪一点?旋转角是多少度?
解:(1) 因为 BC = BD,BA = BE,
所以 BC 和 BD,BA 和 BE 为对应边,
因为△ABC 旋转后能与△EBD 重合,∠ABC = 90°,
所以旋转中心为点 B.
∠ABE 为旋转角,所以旋转角是 90 度.
(2) 结论:AC = DE,AC⊥DE.
理由如下:
因为△ABC 绕点 B 顺时针旋转 90° 后能与△EBD 重合,
所以 DE = AC,DE 与 AC 成 90° 的角,即 AC⊥DE.
(2) AC 与 DE 的关系怎样?请说明理由.
4.如图,画出△ABC绕点C逆时针旋转90°后的图形.
A
B
C
5. 如图,将长方形 ABCD 绕点 A 顺时针旋转到长方形 AB′C′D′ 的位置,旋转角为 a (0° < a < 90°). 若∠1 = 112°,则 a 的大小是 ( )
A. 68° B. 20° C. 28° D. 22°
D
1. 图形旋转的特征是什么?
图形中每一个点都绕着旋转中心旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小都没有发生变化.
课堂小结
2. 如何确定旋转中心与旋转角的方法:
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是在图形外,若在图形上,哪一点在旋转过程中位置没有改变,这一点就是旋转中心;若在图形外,对应点连线的中垂线的交点就是旋转中心.旋转角就是对应线段的夹角或对应点与旋转中心连线的夹角.
10.3.2 旋转的特征
七年级下
华师版
1. 通过具体实例进一步认识旋转,掌握旋转的特征.
2. 经历对具有旋转特征的图形进行观察、分析.
3.会利用旋转的特征解决图形问题.
学习目标
难点
重点
观察下面的图片,想一想它们与基本图形之间有什么关系?是经过怎样变换得到的?
新课引入
观察两个图形,你能发现有哪些线段相等?有哪些角相等?
新知学习
思考并完成填空:
(1) 中,线段 OA、OB 都是绕点 O 旋转 45° 角到对应线段 OA′ 与 OB′,而且 OA = _____,OB = _____,AB = _____;∠AOB = _______,∠A = _____,∠B = _____.
(2) 中,旋转中心是点 O,点 A、B、C 都是绕点 O 旋转 60° 角到对应点 A′、B′、C′,而且 OA = _____,OB = _____,OC = _____;AB = _____,BC = _____,CA = _____;∠CAB = ________,∠ABC = ________,∠BCA = ________.
OA′
OB′
A′B′
∠A′OB′
∠A′
∠B′
OA′
OB′
OC′
A′B′
B′C′
C′A′
∠C′A′B′
∠A′B′C′
∠B′C′A′
(1)
(2)
归纳
图形旋转的特征:
图形中每一个点都绕着旋转中心沿着同一方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小都没有发生变化.
温馨提示
(1) 旋转不改变图形的大小和形状,只改变图形的位置;
(2) 经过旋转,图形上的每一点都绕旋转中心沿相同的方向旋转了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等;
(3) 分析旋转形成的方法:“三个一”,即分析一个中心,一个方向,一个角度.
温馨提示
易错警示:
画旋转图形时容易忽视对旋转方向的要求,除了旋转中心及旋转角之外,还应指明旋转方向是顺时针还是逆时针,若无特别说明,则应考虑两种情况.
例 同学们曾玩过万花筒,它是由三块等长的玻璃片围成的. 如图是在万花筒中看到的一个图案. 图中所有小三角形是大小相同的等边三角形,其中的四边形 AEFG 可以看成是把四边形 ABCD 以 A 为旋转中心 ( )
A. 顺时针旋转 60° 得到 B. 顺时针旋转 120° 得到
C. 逆时针旋转 60° 得到 D. 逆时针旋转 120° 得到
B
分析:根据图形可知∠BAE = 120°,AB 边绕点 A 顺时针旋转 120° 得到 AE 边,所以四边形 AEFG 可以看成是把四边形 ABCD 以 A 为旋转中心顺时针旋转 120° 得到的.
确定旋转中心与旋转角的方法:
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是在图形外,若在图形上,哪一点在旋转过程中位置没有改变,这一点就是旋转中心;若在图形外,对应点连线的中垂线的交点就是旋转中心.旋转角就是对应线段的夹角或对应点与旋转中心连线的夹角.
归纳
1. 如图,△ODC 是由△OAB 绕点 O 顺时针旋转 30° 后得到的图形,若点 D 恰好落在 AB 上,且∠AOC 的度数为 100°,则∠DOB 的度数是
( )
A. 40° B. 30°
C. 38° D. 15°
A
随堂练习
2. 如图,将△AOB 绕点 O 按逆时针方向旋转 45° 后得到△COD,若∠AOB = 15°,则∠AOD 的度数是 _____.
60°
3. 如图所示,△ABC 是直角三角形,延长 AB 到 D,使 BD = BC,在 BC 上取 BE = AB,连结 DE. △ABC 顺时针旋转后能与△EBD 重合,那么
(1) 旋转中心是哪一点?旋转角是多少度?
解:(1) 因为 BC = BD,BA = BE,
所以 BC 和 BD,BA 和 BE 为对应边,
因为△ABC 旋转后能与△EBD 重合,∠ABC = 90°,
所以旋转中心为点 B.
∠ABE 为旋转角,所以旋转角是 90 度.
(2) 结论:AC = DE,AC⊥DE.
理由如下:
因为△ABC 绕点 B 顺时针旋转 90° 后能与△EBD 重合,
所以 DE = AC,DE 与 AC 成 90° 的角,即 AC⊥DE.
(2) AC 与 DE 的关系怎样?请说明理由.
4.如图,画出△ABC绕点C逆时针旋转90°后的图形.
A
B
C
5. 如图,将长方形 ABCD 绕点 A 顺时针旋转到长方形 AB′C′D′ 的位置,旋转角为 a (0° < a < 90°). 若∠1 = 112°,则 a 的大小是 ( )
A. 68° B. 20° C. 28° D. 22°
D
1. 图形旋转的特征是什么?
图形中每一个点都绕着旋转中心旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小都没有发生变化.
课堂小结
2. 如何确定旋转中心与旋转角的方法:
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是在图形外,若在图形上,哪一点在旋转过程中位置没有改变,这一点就是旋转中心;若在图形外,对应点连线的中垂线的交点就是旋转中心.旋转角就是对应线段的夹角或对应点与旋转中心连线的夹角.
