10.4中心对称 课件(共29张PPT)
文档属性
| 名称 | 10.4中心对称 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
10.4 中心对称
七年级下
华师版
1. 理解成中心对称的两个图形与中心对称图形的概念,并且知道两者之间的区别与联系.
2. 掌握它们的性质,会判断两个图形是否成中心对称,会画一个图形关于一个点成中心对称的图形.
学习目标
难点
重点
在上一节,我们已经看到有不少图形绕某一中心旋转一定角度后,可以与自身重合. 如图所示的三个图形都是这样的旋转对称图形.
上面图形中哪个图形旋转 180° 后能与自身重合?
你能举出日常生活中旋转 180° 后能与自身重合的例子吗?
图 2 旋转 180° 可以与自身重合.
新课引入
像图 2 这样,把一个图形绕着中心旋转 180° 后能与自身重合,我们把这种图形叫做中心对称图形. 这个中心叫做对称中心. 所以,中心对称图形是旋转角度是 180° 的旋转对称图形.
归纳
新知学习
思考
线段、三角形、平行四边形、正方形、圆分别是中心对称图形吗?如果是,那么对称中心又分别在哪里?
线段是中心对称图形,对称中心是线段的中点.
平行四边形是中心对称图形,对称中心是对角线的交点.
正方形是中心对称图形,对称中心是对角线的交点.
圆形是中心对称图形,对称中心是圆心.
温馨提示
(1) 中心对称图形的对称中心一定在图形内;
(2) 中心对称图形是针对一个图形而言的;
(3) 中心对称图形上所有的点关于对称中心的对称点都在这个图形本身上;
(4) 中心对称图形一定是旋转对称图形,但旋转对称图形不一定是中心对称图形;
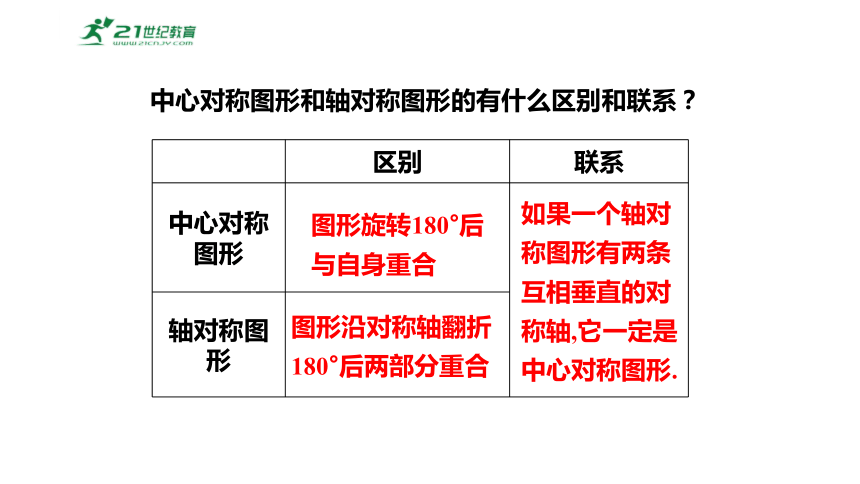
区别 联系
中心对称图形
轴对称图形 图形旋转180°后与自身重合
图形沿对称轴翻折180°后两部分重合
如果一个轴对称图形有两条互相垂直的对称轴,它一定是中心对称图形.
中心对称图形和轴对称图形的有什么区别和联系?
例1 五星红旗上的每一个五角星 ( )
A. 是轴对称图形,但不是中心对称图形
B. 是中心对称图形,但不是轴对称图形
C. 既是轴对称图形,又是中心对称图形
D. 既不是轴对称图形,也不是中心对称图形
A
探究
你能根据两个图形成轴对称的定义总结一下什么叫两个图形成中心对称吗?
把一个图形绕着某一点旋转 180°,如果它能够和另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
观察图形,并回答相应问题:
1. 这个图形是中心对称图形吗?
2. △ABC 与△ADE 有什么特点吗?
是中心对称图形.
△ABC旋转180°后和△ADE重合.
探究
你能根据中心对称和两个图形成轴对称的定义总结一下△ABC 与△ADE的这种特点吗?
归纳
把一个图形绕着某一点旋转 180°,如果它能够和另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
3. △ABC 与△ADE 是成中心对称的两个三角形,点 A 是对称中心,点 B 关于对称中心 A 的对称点为 _____,点 C 关于对称中心 A 的对称点是 _____,点 A 关于对称中心 A 的对称点为 _____,B、A、D 在 ___________ 上,AD = _____,C、A、E 在 ___________ 上,AC = _____,ED ______________.
D
E
A
同一条直线
AB
AE
同一条直线
平行且等于 CB
例2 如下所示的 4 组图形中,左边数字与右边数字成中心对称的有( )
A. 1 组 B. 2 组 C. 3 组 D. 4 组
C
探究
观察图形:
(1) △ABC 与△A′B′C′ 关于点 O 成中心对称吗?
两三角形成中心对称.
(2) 在同一直线上的三点分别是 _____、______、______. AO = _____,BO = _____,CO = _____,AB = _____,AC = _____,BC = _____.
AOA′
BOB′
COC′
A′O
B′O
C′O
A′B′
A′C′
B′C′
归纳
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反之,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
填写下表:
区别 联系
成中心对称
中心对称图形 ① 成中心对称是指两个图形的关系,中心对称图形是指具有某种性质的图形.
② 成中心对称的两个图形的对称点分别在两个图形上,中心对称图形的对称点在一个图形上.
若把中心对称图形的两部分看成两个图形,则它们成中心对称;若把成中心对称的两个图形看成一个整体,那么这个整体也就是中心对称图形.
例3 如图,已知△ABC 和点 O,画出△DEF,使△DEF 和△ABC 关于点 O 成中心对称.
解:(1) 连结 AO 并延长 AO 到点 D,使 OD = OA,于是得到点 A 关于点 O 的对称点 D;
(2) 同样画出点 B 和点 C 关于点 O 的对称点 E 和 F;
(3) 顺次连结 DE、EF、FD. 如图,△DFF 即为所求的三角形.
A
B
C
O
D
E
F
如图,已知 △ABC 与 △A′B′C′ 中心对称,找出它们的对称中心 O.
A
B
C
A′
B′
C′
试一试
解法1:根据观察,B、B′ 应是对应点,连接 BB′,用圆规找出 BB′ 的中点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
解法 2:根据观察,B、B′ 及 C、C′ 应是两组对应点,连接 BB′、CC′,BB′、CC′ 相交于点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
注意:如果限制只用直尺作图,我们用解法 2
随堂练习
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1.仔细观察下面图片所列的26个英文字母,将相应的字母填入表中适当的空格内.
对称形式 轴对称 旋转对称 中心对称
只有一条对称轴 有两条对称轴 英文字母
ABCDEMTUVWY
HIOX
HINOSXZ
HINOSXZ
2. 如图,已知 △AOB 与 △DOC 成中心对称,△AOB 的面积是 6,AB=3,则△DOC 中 CD边上的高是( )
A. 2 B. 4
C. 6 D. 8
B
A
B
C
D
O
3.朝阳广场有一个用地砖铺设的太极图图案,如图,图案整体是一个大圆,其中黑色部分和白色部分关于大圆的圆心成中心对称,已知黑色部分的面积为24 m2,则这个太极图图案的直径为____ m(π取3).
8
4.如图,已知四边形 ABCD 和点O,画四边形 A′B′C′D′,使四边形 A′B′C′D′ 和四边形ABCD 关于点 O 成中心对称.
A
B
C
D
A′
B′
C′
D′
O
1. 什么是中心对称图形?
把一个图形绕着中心旋转 180° 后能与自身重合,我们把这种图形叫做中心对称图形. 这个中心叫做对称中心.
2. 什么是两图形成中心对称?
把一个图形绕着某一点旋转 180°,如果它能够和另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
课堂小结
3. 成中心对称的两图形有什么特点?怎样判定两图形是否成中心对称?
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反之,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
区别 联系
中心对称图形
轴对称图形 图形旋转180°后与自身重合
图形沿对称轴翻折180°后两部分重合
如果一个轴对称图形有两条互相垂直的对称轴,它一定是中心对称图形.
中心对称图形和轴对称图形的有什么区别和联系?
成中心对称和中心对称对称图形的有什么区别和联系?
区别 联系
成中心对称
中心对称图形 ① 成中心对称是指两个图形的关系,中心对称图形是指具有某种性质的图形.
② 成中心对称的两个图形的对称点分别在两个图形上,中心对称图形的对称点在一个图形上.
若把中心对称图形的两部分看成两个图形,则它们成中心对称;若把成中心对称的两个图形看成一个整体,那么这个整体也就是中心对称图形.
10.4 中心对称
七年级下
华师版
1. 理解成中心对称的两个图形与中心对称图形的概念,并且知道两者之间的区别与联系.
2. 掌握它们的性质,会判断两个图形是否成中心对称,会画一个图形关于一个点成中心对称的图形.
学习目标
难点
重点
在上一节,我们已经看到有不少图形绕某一中心旋转一定角度后,可以与自身重合. 如图所示的三个图形都是这样的旋转对称图形.
上面图形中哪个图形旋转 180° 后能与自身重合?
你能举出日常生活中旋转 180° 后能与自身重合的例子吗?
图 2 旋转 180° 可以与自身重合.
新课引入
像图 2 这样,把一个图形绕着中心旋转 180° 后能与自身重合,我们把这种图形叫做中心对称图形. 这个中心叫做对称中心. 所以,中心对称图形是旋转角度是 180° 的旋转对称图形.
归纳
新知学习
思考
线段、三角形、平行四边形、正方形、圆分别是中心对称图形吗?如果是,那么对称中心又分别在哪里?
线段是中心对称图形,对称中心是线段的中点.
平行四边形是中心对称图形,对称中心是对角线的交点.
正方形是中心对称图形,对称中心是对角线的交点.
圆形是中心对称图形,对称中心是圆心.
温馨提示
(1) 中心对称图形的对称中心一定在图形内;
(2) 中心对称图形是针对一个图形而言的;
(3) 中心对称图形上所有的点关于对称中心的对称点都在这个图形本身上;
(4) 中心对称图形一定是旋转对称图形,但旋转对称图形不一定是中心对称图形;
区别 联系
中心对称图形
轴对称图形 图形旋转180°后与自身重合
图形沿对称轴翻折180°后两部分重合
如果一个轴对称图形有两条互相垂直的对称轴,它一定是中心对称图形.
中心对称图形和轴对称图形的有什么区别和联系?
例1 五星红旗上的每一个五角星 ( )
A. 是轴对称图形,但不是中心对称图形
B. 是中心对称图形,但不是轴对称图形
C. 既是轴对称图形,又是中心对称图形
D. 既不是轴对称图形,也不是中心对称图形
A
探究
你能根据两个图形成轴对称的定义总结一下什么叫两个图形成中心对称吗?
把一个图形绕着某一点旋转 180°,如果它能够和另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
观察图形,并回答相应问题:
1. 这个图形是中心对称图形吗?
2. △ABC 与△ADE 有什么特点吗?
是中心对称图形.
△ABC旋转180°后和△ADE重合.
探究
你能根据中心对称和两个图形成轴对称的定义总结一下△ABC 与△ADE的这种特点吗?
归纳
把一个图形绕着某一点旋转 180°,如果它能够和另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
3. △ABC 与△ADE 是成中心对称的两个三角形,点 A 是对称中心,点 B 关于对称中心 A 的对称点为 _____,点 C 关于对称中心 A 的对称点是 _____,点 A 关于对称中心 A 的对称点为 _____,B、A、D 在 ___________ 上,AD = _____,C、A、E 在 ___________ 上,AC = _____,ED ______________.
D
E
A
同一条直线
AB
AE
同一条直线
平行且等于 CB
例2 如下所示的 4 组图形中,左边数字与右边数字成中心对称的有( )
A. 1 组 B. 2 组 C. 3 组 D. 4 组
C
探究
观察图形:
(1) △ABC 与△A′B′C′ 关于点 O 成中心对称吗?
两三角形成中心对称.
(2) 在同一直线上的三点分别是 _____、______、______. AO = _____,BO = _____,CO = _____,AB = _____,AC = _____,BC = _____.
AOA′
BOB′
COC′
A′O
B′O
C′O
A′B′
A′C′
B′C′
归纳
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反之,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
填写下表:
区别 联系
成中心对称
中心对称图形 ① 成中心对称是指两个图形的关系,中心对称图形是指具有某种性质的图形.
② 成中心对称的两个图形的对称点分别在两个图形上,中心对称图形的对称点在一个图形上.
若把中心对称图形的两部分看成两个图形,则它们成中心对称;若把成中心对称的两个图形看成一个整体,那么这个整体也就是中心对称图形.
例3 如图,已知△ABC 和点 O,画出△DEF,使△DEF 和△ABC 关于点 O 成中心对称.
解:(1) 连结 AO 并延长 AO 到点 D,使 OD = OA,于是得到点 A 关于点 O 的对称点 D;
(2) 同样画出点 B 和点 C 关于点 O 的对称点 E 和 F;
(3) 顺次连结 DE、EF、FD. 如图,△DFF 即为所求的三角形.
A
B
C
O
D
E
F
如图,已知 △ABC 与 △A′B′C′ 中心对称,找出它们的对称中心 O.
A
B
C
A′
B′
C′
试一试
解法1:根据观察,B、B′ 应是对应点,连接 BB′,用圆规找出 BB′ 的中点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
解法 2:根据观察,B、B′ 及 C、C′ 应是两组对应点,连接 BB′、CC′,BB′、CC′ 相交于点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
注意:如果限制只用直尺作图,我们用解法 2
随堂练习
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1.仔细观察下面图片所列的26个英文字母,将相应的字母填入表中适当的空格内.
对称形式 轴对称 旋转对称 中心对称
只有一条对称轴 有两条对称轴 英文字母
ABCDEMTUVWY
HIOX
HINOSXZ
HINOSXZ
2. 如图,已知 △AOB 与 △DOC 成中心对称,△AOB 的面积是 6,AB=3,则△DOC 中 CD边上的高是( )
A. 2 B. 4
C. 6 D. 8
B
A
B
C
D
O
3.朝阳广场有一个用地砖铺设的太极图图案,如图,图案整体是一个大圆,其中黑色部分和白色部分关于大圆的圆心成中心对称,已知黑色部分的面积为24 m2,则这个太极图图案的直径为____ m(π取3).
8
4.如图,已知四边形 ABCD 和点O,画四边形 A′B′C′D′,使四边形 A′B′C′D′ 和四边形ABCD 关于点 O 成中心对称.
A
B
C
D
A′
B′
C′
D′
O
1. 什么是中心对称图形?
把一个图形绕着中心旋转 180° 后能与自身重合,我们把这种图形叫做中心对称图形. 这个中心叫做对称中心.
2. 什么是两图形成中心对称?
把一个图形绕着某一点旋转 180°,如果它能够和另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
课堂小结
3. 成中心对称的两图形有什么特点?怎样判定两图形是否成中心对称?
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反之,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
区别 联系
中心对称图形
轴对称图形 图形旋转180°后与自身重合
图形沿对称轴翻折180°后两部分重合
如果一个轴对称图形有两条互相垂直的对称轴,它一定是中心对称图形.
中心对称图形和轴对称图形的有什么区别和联系?
成中心对称和中心对称对称图形的有什么区别和联系?
区别 联系
成中心对称
中心对称图形 ① 成中心对称是指两个图形的关系,中心对称图形是指具有某种性质的图形.
② 成中心对称的两个图形的对称点分别在两个图形上,中心对称图形的对称点在一个图形上.
若把中心对称图形的两部分看成两个图形,则它们成中心对称;若把成中心对称的两个图形看成一个整体,那么这个整体也就是中心对称图形.
