2024年山东省济南市九年级学业水平考试数学综合模拟试题(含答案)
文档属性
| 名称 | 2024年山东省济南市九年级学业水平考试数学综合模拟试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 914.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-11 21:22:10 | ||
图片预览




文档简介
济南市2024年九年级学业水平考试
数学综合试题模拟
一、选择题(本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂写在答题卡上,每小题选对得4分,共40分)
1.﹣2024的相反数是
A.﹣2024 B.2024 C.±2024 D.
2.三个大小相同的正方体搭成的几何体如图所示,其主视图是
A. B. C. D.
3.2024年元旦假期的到来,点燃了消费者的出游热情,也激发了旅游市场的活力.元旦假期三天,长沙市共接待游客609.65万人次.数据“609.65万”用科学记数法表示为
A.0.60965×108 B.6.0965×107 C.60.965×106 D.6.0965×106
4.近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了护眼灯,其侧面示意图(台灯底座高度忽略不计)如图所示,其中BC⊥AB,ED∥AB,经使用发现,当∠DCB=140°时,台灯光线最佳.则此时∠EDC的度数为
A.130° B.120° C.110° D.100°
5.若有理数a、b、c在数轴上的位置如图所示,
则|a+b|+|c﹣a|=
A.b+c B.﹣b﹣c C.﹣2a﹣b+c D.b﹣c
6.如图,一个钟摆的摆长OA的长为a,当钟摆从最左侧摆到最右侧时,摆角∠AOB为2x,点C是AB的中点,OC与AB交于点D,则CD的长为
A.asin2x B.acos2x
C.a(1﹣sinx) D.a(1﹣cosx)
7.近几年,二维码逐渐进入了人们的生活,成为广大民众生活中不可或缺的一部分.小刚现将二维码打印在面积为200cm2的正方形纸片上,如图,为了估计黑色阴影部分的面积,他在纸内随机掷点,经过大量实验,发现点落在黑色阴影的频率稳定在0.6左右,则据此估计此二维码中黑色阴影的面积为
A.0.4cm2 B.0.6cm2 C.180cm2 D.120cm2
8.如图,在△ABC中,∠ABC=60°,∠C=45°,以点B为圆心,任意长为半径画弧,分别交BA、BC于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连结BP交AC于点D.若AB=2,则CD的长为
A. B. C. D.
9.已知点M(﹣2,y1),N(﹣1,y2)均在反比例函数的图象上,则y1与y2的大小关系为
A.y1>y2 B.y1=y2 C.y1<y2 D.y1≤y2
10.已知抛物线y=ax2+bx+c(a,b,c是常数)开口向下,过A(﹣1,0),B(m,0)两点,且1<m<2.下列四个结论:
①b>0; ②若时,则3a+2c<0;
③若点M(x1,y1),N(x2,y2),在抛物线上,x1<x2,且x1+x2>1,则y1>y2;
④当a ﹣1时,关于x的一元二次方程ax2+bx+c=1必有两个不相等的实数根.
其中结论正确的结论有
A.①③ B.①② C.③④ D.①③④
二、填空题(本大题共6个小题,每小题4分,共24分.请直接写答案.)
11.分解因式:m2﹣36=__________.
12.某学校开设了劳动教育课程,小明从感兴趣的“陶艺”“电工”“烹饪”3门课程中随机选择一门学习,每门课程被选中的可能性相等,小明恰好选中“陶艺”的概率为__________.
13.若关于x的一元二次方程ax2+bx+5=0(a≠0)的一个解是x=1,则2019﹣a﹣b的值是_________________.
14.《九章算术》中有这样一道题:“今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其大意为:今有一圆柱形木材埋在墙壁中,不知其大小.设其横截面为⊙O,用锯子去锯这个木材,锯口深AB为1寸,锯道长CD为1尺.由此可得这块圆柱形木材横截面的直径是___________尺.(注:1尺=10寸)
第14题图 第15题图 第16题图
15.在“探索一次函数y=kx+b的系数k,b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,0),B(1,2),C(3,3).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式y1=k1x+b1,y2=k2x+b2,y3=k3x+b3,请分别计算2k1+b1,2k2+b2,2k3+b3的值,其中最小的值为_________________.
16.平面直角坐标系中,C(0,4),K(2,0),A为x轴上一动点,连接AC,将AC绕A点顺时针旋转90°得到AB,当点A在x轴上运动,BK取最小值时,点B的坐标为_________________.
三、解答题(本大题共10小题,共86分,解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分6分)
计算:.
18.(本小题满分6分)
解不等式组,把解集在数轴上表示出来,并写出整数解.
19.(本小题满分6分)
如图,在 ABCD中,点E在边BC上,连接AE,过点C作CF⊥AD于点F,且AF=CE.请判断四边形AECF的形状,并说明理由.
20.(本小题满分8分)
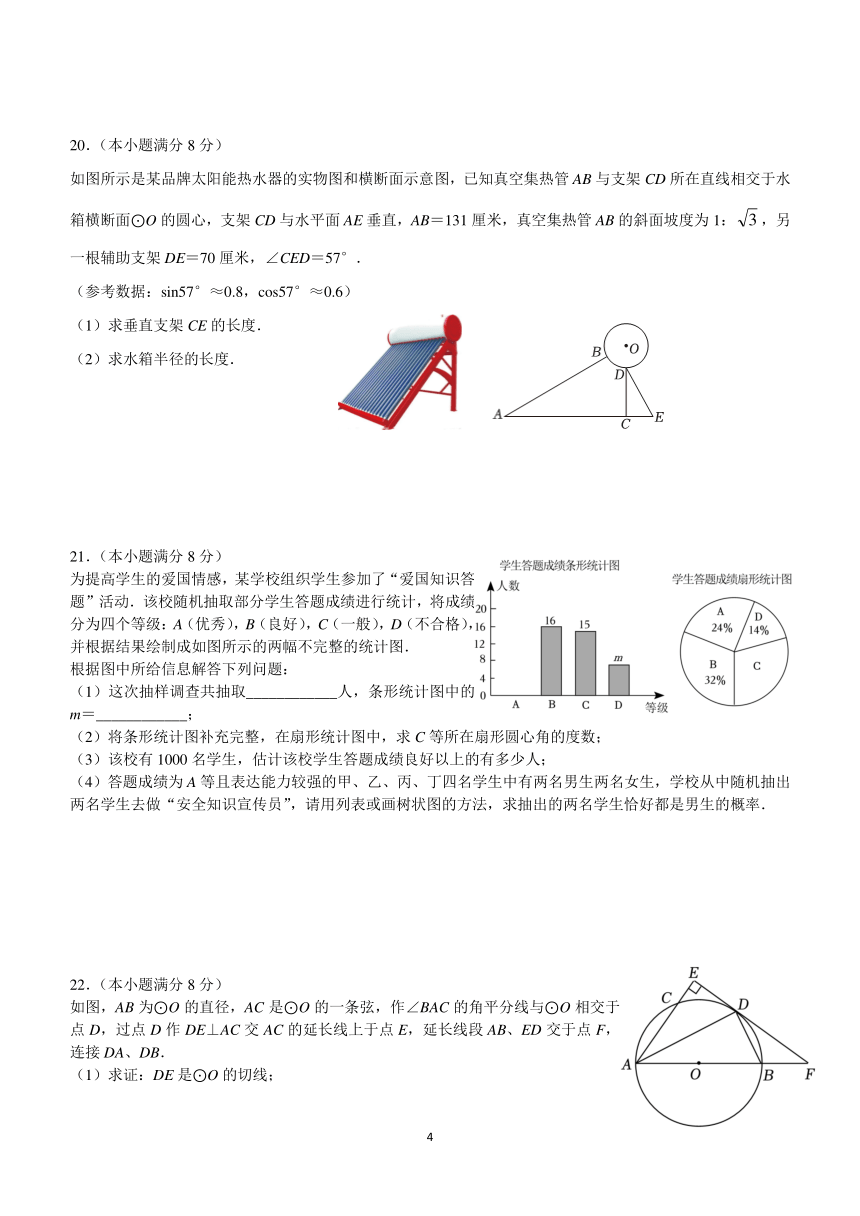
如图所示是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平面AE垂直,AB=131厘米,真空集热管AB的斜面坡度为1:,另一根辅助支架DE=70厘米,∠CED=57°.
(参考数据:sin57°≈0.8,cos57°≈0.6)
(1)求垂直支架CE的长度.
(2)求水箱半径的长度.
21.(本小题满分8分)
为提高学生的爱国情感,某学校组织学生参加了“爱国知识答题”活动.该校随机抽取部分学生答题成绩进行统计,将成绩分为四个等级:A(优秀),B(良好),C(一般),D(不合格),并根据结果绘制成如图所示的两幅不完整的统计图.
根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取____________人,条形统计图中的m=____________;
(2)将条形统计图补充完整,在扇形统计图中,求C等所在扇形圆心角的度数;
(3)该校有1000名学生,估计该校学生答题成绩良好以上的有多少人;
(4)答题成绩为A等且表达能力较强的甲、乙、丙、丁四名学生中有两名男生两名女生,学校从中随机抽出两名学生去做“安全知识宣传员”,请用列表或画树状图的方法,求抽出的两名学生恰好都是男生的概率.
22.(本小题满分8分)
如图,AB为⊙O的直径,AC是⊙O的一条弦,作∠BAC的角平分线与⊙O相交于点D,过点D作DE⊥AC交AC的延长线上于点E,延长线段AB、ED交于点F,连接DA、DB.
(1)求证:DE是⊙O的切线;
(2)若AB=10,,求BF.
23.(本小题满分10分)
为推进全民健身设施建设,某体育中心准备改扩建一块运动场地.现有甲、乙两个工程队参与施工,具体信息如下:
信息一
工程队 每天施工面积(单位:m2) 每天施工费用(单位:元)
甲 x+300 3600
乙 x 2200
信息二
甲工程队施工1800m2所需天数与乙工程队施工1200m2所需天数相等.
(1)求x的值;
(2)该工程计划先由甲工程队单独施工若干天,再由乙工程队单独继续施工,两队共施工22天,且完成的施工面积不少于15000m2.该段时间内体育中心至少需要支付多少施工费用?
24.(本小题满分10分)
阅读与思考:下面是小亮同学的一篇数学日记,请仔细阅读并完成相应的任务.
今天是2023年12月4日(星期一),在下午数学活动课上,我们“腾飞”小组的同学参加了人教九年级下册19页“活动2”的探究活动.如图,取一根长100cm的匀质木杆,用细绳绑在木杆的中点O并将其吊起来,在中点O的左侧距离中点O25cm处挂一个重9.8N的物体,在中点O右侧用一个弹簧秤向下拉,使木杆处于水平状态,改变弹簧秤与中点O的距离l(单位:cm),看弹簧秤的示数F(单位,N)有什么变化.第一步,实验测量.改变弹簧秤与中点O的距离L,观察弹簧秤的示数F的值,并做好记录(共记录了7组数据).第二步,整理数据.第一组第二组第三组第四组第五组第六组第七组L/cm…5101420253540…F/N…4924.517.512.259.886.125…第三步,描点连线.以L的数值为横坐标,对应F的数值为纵坐标在平面直角坐标系中描出以表中数对为坐标的各点,并用平滑的曲线顺次连接这些点.在数据分析时,我发现一个数据有错误,重新测量计算后,证明了我的猜想正确,并修改了表中这个数据.实验结束后,大家都有很多收获,每人都撰写了日记.
任务:(1)你认为表中第几组数据是错误的?请把这组数据改正过来:
(2)在平面直角坐标系中,画出F与L的函数图象:
(3)这条曲线是反比例函数的一支吗?为什么?并直接写出F关于L的函数表达式;
(4)点(50,4.9)在这条曲线上吗?说明理由.
25.(本小题满分12分)
如图1,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0)与y轴交于点C.
(1)求抛物线的函数表达式.
(2)如图2,当点P从点B匀速运动到点O时,过点P作PF⊥AB交抛物线于点F,交直线BC于点E,连结CF.求S△CBF的最大值.
(3)若点P从点B匀速运动到点A时,点Q恰好从点C运动到点O,作点Q关于直线BC的对称点Q',当点Q'落在△CEF的一条边上时,请直接写出CQ的长度.
26.(本小题满分12分)
综合与实践:
问题背景:借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究.
如图1,在△ABC中,∠B=90°,AB=BC=4,分别取AB,AC的中点D,E,作△ADE.如图2所示,将△ADE绕点A逆时针旋转,连结BD,CE.
(1)探究发现
旋转过程中,线段BD和CE的长度存在怎样的数量关系?写出你的猜想,并证明.
(2)性质应用
如图3,当DE所在直线首次经过点B时,求CE的长.
(3)延伸思考
如图4,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,分别取AB,BC的中点D,E、作△BDE.将△BDE绕点B逆时针旋转,连接AD,CE.当边AB平分线段DE时,求tan∠ECB的值.
济南市2024年九年级学业水平考试
数学综合试题模拟参考答案
一、选择题(本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂写在答题卡上,每小题选对得4分,选错、不选或选出的答案超过一个均记0分,共40分)
1.B 2.B 3.D 4.A 5.B 6.D 7.D 8.B 9.C 10.D
二、填空题(本大题共6个小题,每小题4分,共24分.请直接写答案.)
11.(m﹣6)(m+6) 12. 13.2024
14.2.6 15.2 16.(3,﹣1)
三、解答题(本大题共10小题,共86分,解答应写出文字说明,证明过程或演算步骤.)
17.解:原式=11+22.
18.解:,
解不等式①得,x≤2,
解不等式②得,x>﹣1,
∴不等式组的解集是﹣1<x≤2,
在数轴上表示为
,
∴不等式组的整数解是:0,1,2.
19.解:四边形AECF是矩形,
理由:∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠D=∠B,
∵AF=CE,
∴AD﹣AF=CB﹣CE,
∴DF=BE,
在△CDF和△ABE中,
,
∴△CDF和≌△ABE(SAS),
∴CF=AE,
∴四边形AECF是平行四边形,
∵作CF⊥AD于点F,
∴∠AFC=90°,
∴四边形AECF是矩形.
20.解:(1)在Rt△DCE中,DE=70厘米,∠CED=57°,
∵cos∠CED,
∴CE=DE cos∠CED≈70×0.6=42(厘米),
答:支架CE的长度约为42厘米;
(2)设水箱半径的长度为x厘米,
在Rt△DCE中,DE=70厘米,∠CED=57°,
∵sin∠CED,
∴CD=DE sin∠CED≈70×0.8=56(厘米),
∵斜面AB坡度为1:,
∴tanA,
∴∠A=30°,
∵sinA,
∴,
解得:x=19,
经检验,x=19是原方程的根,
答:水箱半径的长度约为19厘米.
21.解:(1)50,7;
(2)由(1)知,m=7,
等级为A的有:50﹣16﹣15﹣7=12(人),
补充完整的条形统计图如图所示,
C等所在扇形圆心角的度数为:360°108°;
(3)1000×(24%+32%)
=1000×56%
=560(人),
即估计该校学生答题成绩良好以上的有560人;
(4)树状图如下所示:
由上可得,一共存在12种等可能性,其中抽出的两名学生恰好都是男生的可能性有2种,
∴抽出的两名学生恰好都是男生的概率为.
22.(1)证明:连接OD,
∵∠BAC 的角平分线与⊙O 交于点D,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴AC∥DO,
∵DE⊥AC,
∴∠E=90°,
∴∠ODF=∠E=90°,
∴OD⊥DE,
∵OD是⊙O的半径,OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=10,,
∴BD2,
过点D作 DM⊥AB于点M,
∵S△ABD,
∴DM4,
∴AM8,
设BF=x,
∵∠BAC 的角平分线与⊙O 交于点D,DE⊥AC,DM⊥AB,
∴DE=DM,
∴CD=BD,
在Rt△AED和Rt△AMD中,
,
Rt△AED≌Rt△AMD(HL),
∴AE=AM,
∵DM=4,
∴DE=DM=4,
∵AM=8
∴AE=AM=8,
∵∠F=∠F,∠ODF=∠E=90°,
∴△FDO∽△FEA,
∴,
∴,
∴x,
∴BF.
23.解:(1)根据题意得:,
解得:x=600,
经检验,x=600是所列方程的解,且符合题意.
答:x的值为600;
(2)设甲工程队施工m天,则乙工程队单独施工(22﹣m)天,
根据题意得:(600+300)m+600(22﹣m)≥15000,
解得:m≥6,
设该段时间内体育中心需要支付w元施工费用,则w=3600m+2200(22﹣m),
即w=1400m+48400,
∵1400>0,
∴w随m的增大而增大,
∴当m=6时,w取得最小值,最小值=1400×6+48400=56800.
答:该段时间内体育中心至少需要支付56800元施工费用.
24.解:(1)根据表中数据,可发现L与F的乘积为定值245,
所以第六组数据是错误的,
正确应该是:L=35时,F=7;
(2)画出F与L的函数图象如图:
(3)因为F、L都是正数,
所以这条曲线是反比例函数的一支,
因为 FL=245,
其函数表达式为:F;
(4)因为50×4.9=245,
∴点(50,4.9)在这条曲线上.
25.解:(1)将点A(﹣1,0),B(3,0)代入y=﹣x2+bx+c,
得,
解得,
∴抛物线的函数表达式为y=﹣x2+2x+3;
(2)把x=0代入y=﹣x2+2x+3,得y=3,
∴点C的坐标为(0,3),
设直线BC的解析式为y=kx+b,
把B(3,0),C(0,3)代入,
得,
解得,
∴直线BC的解析式为y=﹣x+3,
设点P的坐标为(m,0),
由过点P作PF⊥AB交抛物线于点F,交直线BC于点E,得E(m,﹣m+3),F(m,﹣m2+2m+3),
由点P从点B匀速运动到点,得点E和F均在第一象限,
∴EF=(﹣m2+2m+3)﹣(﹣m+3)=﹣m2+3m(0<m<3),
当时,EF取得最大值,
∵S△CBF=S△CEF+S△BEF,
∴S△CBF的最大值为;
(3).
26.解:(1)CE,理由如下:
∵∠B=90°,AB=BC,
∴ACAB,
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
∵,
∴△ABD∽△ACE,
∴,
∴CE;
(2)由(1)知:△ABD∽△ACE,
∴∠ABE=∠ACE,∠ADE=∠AEC,∠ADB=∠AEC,
∴点A、B、C、E共圆,
∴∠AEC+∠ABC=180°,∠BCE=∠BAC=45°,
∵∠ABC=90°,
∴∠ADB=∠AEC=90°,
∴∠AEB=45°,
∵AB=4,AD=2,
∴AEAD=2,
∴CE2;
(3)如图,
设AB与DE相交于点Q,作EF⊥BC于F,
∵△DBE∽△ABC,
∴∠BED=∠ACB,∠DBE=∠ABC=90°,
∵AB平分DE,
∴DQ=QE,
∴BQ=EQQE,
∴∠ABE=∠DEB=∠ACB,
∵∠ABE+∠CBE=90°,∠CBE+∠BEG=90°,
∴∠ABE=∠BEG,
∴∠BEG=∠ACB,
∴BG=BE sin∠BEG=3 sin∠ACB=3,
EG=BE cos∠BEG=3,
∴CG=BC﹣BG=6,
∴tan∠ECB.
数学综合试题模拟
一、选择题(本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂写在答题卡上,每小题选对得4分,共40分)
1.﹣2024的相反数是
A.﹣2024 B.2024 C.±2024 D.
2.三个大小相同的正方体搭成的几何体如图所示,其主视图是
A. B. C. D.
3.2024年元旦假期的到来,点燃了消费者的出游热情,也激发了旅游市场的活力.元旦假期三天,长沙市共接待游客609.65万人次.数据“609.65万”用科学记数法表示为
A.0.60965×108 B.6.0965×107 C.60.965×106 D.6.0965×106
4.近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了护眼灯,其侧面示意图(台灯底座高度忽略不计)如图所示,其中BC⊥AB,ED∥AB,经使用发现,当∠DCB=140°时,台灯光线最佳.则此时∠EDC的度数为
A.130° B.120° C.110° D.100°
5.若有理数a、b、c在数轴上的位置如图所示,
则|a+b|+|c﹣a|=
A.b+c B.﹣b﹣c C.﹣2a﹣b+c D.b﹣c
6.如图,一个钟摆的摆长OA的长为a,当钟摆从最左侧摆到最右侧时,摆角∠AOB为2x,点C是AB的中点,OC与AB交于点D,则CD的长为
A.asin2x B.acos2x
C.a(1﹣sinx) D.a(1﹣cosx)
7.近几年,二维码逐渐进入了人们的生活,成为广大民众生活中不可或缺的一部分.小刚现将二维码打印在面积为200cm2的正方形纸片上,如图,为了估计黑色阴影部分的面积,他在纸内随机掷点,经过大量实验,发现点落在黑色阴影的频率稳定在0.6左右,则据此估计此二维码中黑色阴影的面积为
A.0.4cm2 B.0.6cm2 C.180cm2 D.120cm2
8.如图,在△ABC中,∠ABC=60°,∠C=45°,以点B为圆心,任意长为半径画弧,分别交BA、BC于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连结BP交AC于点D.若AB=2,则CD的长为
A. B. C. D.
9.已知点M(﹣2,y1),N(﹣1,y2)均在反比例函数的图象上,则y1与y2的大小关系为
A.y1>y2 B.y1=y2 C.y1<y2 D.y1≤y2
10.已知抛物线y=ax2+bx+c(a,b,c是常数)开口向下,过A(﹣1,0),B(m,0)两点,且1<m<2.下列四个结论:
①b>0; ②若时,则3a+2c<0;
③若点M(x1,y1),N(x2,y2),在抛物线上,x1<x2,且x1+x2>1,则y1>y2;
④当a ﹣1时,关于x的一元二次方程ax2+bx+c=1必有两个不相等的实数根.
其中结论正确的结论有
A.①③ B.①② C.③④ D.①③④
二、填空题(本大题共6个小题,每小题4分,共24分.请直接写答案.)
11.分解因式:m2﹣36=__________.
12.某学校开设了劳动教育课程,小明从感兴趣的“陶艺”“电工”“烹饪”3门课程中随机选择一门学习,每门课程被选中的可能性相等,小明恰好选中“陶艺”的概率为__________.
13.若关于x的一元二次方程ax2+bx+5=0(a≠0)的一个解是x=1,则2019﹣a﹣b的值是_________________.
14.《九章算术》中有这样一道题:“今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其大意为:今有一圆柱形木材埋在墙壁中,不知其大小.设其横截面为⊙O,用锯子去锯这个木材,锯口深AB为1寸,锯道长CD为1尺.由此可得这块圆柱形木材横截面的直径是___________尺.(注:1尺=10寸)
第14题图 第15题图 第16题图
15.在“探索一次函数y=kx+b的系数k,b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,0),B(1,2),C(3,3).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式y1=k1x+b1,y2=k2x+b2,y3=k3x+b3,请分别计算2k1+b1,2k2+b2,2k3+b3的值,其中最小的值为_________________.
16.平面直角坐标系中,C(0,4),K(2,0),A为x轴上一动点,连接AC,将AC绕A点顺时针旋转90°得到AB,当点A在x轴上运动,BK取最小值时,点B的坐标为_________________.
三、解答题(本大题共10小题,共86分,解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分6分)
计算:.
18.(本小题满分6分)
解不等式组,把解集在数轴上表示出来,并写出整数解.
19.(本小题满分6分)
如图,在 ABCD中,点E在边BC上,连接AE,过点C作CF⊥AD于点F,且AF=CE.请判断四边形AECF的形状,并说明理由.
20.(本小题满分8分)
如图所示是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平面AE垂直,AB=131厘米,真空集热管AB的斜面坡度为1:,另一根辅助支架DE=70厘米,∠CED=57°.
(参考数据:sin57°≈0.8,cos57°≈0.6)
(1)求垂直支架CE的长度.
(2)求水箱半径的长度.
21.(本小题满分8分)
为提高学生的爱国情感,某学校组织学生参加了“爱国知识答题”活动.该校随机抽取部分学生答题成绩进行统计,将成绩分为四个等级:A(优秀),B(良好),C(一般),D(不合格),并根据结果绘制成如图所示的两幅不完整的统计图.
根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取____________人,条形统计图中的m=____________;
(2)将条形统计图补充完整,在扇形统计图中,求C等所在扇形圆心角的度数;
(3)该校有1000名学生,估计该校学生答题成绩良好以上的有多少人;
(4)答题成绩为A等且表达能力较强的甲、乙、丙、丁四名学生中有两名男生两名女生,学校从中随机抽出两名学生去做“安全知识宣传员”,请用列表或画树状图的方法,求抽出的两名学生恰好都是男生的概率.
22.(本小题满分8分)
如图,AB为⊙O的直径,AC是⊙O的一条弦,作∠BAC的角平分线与⊙O相交于点D,过点D作DE⊥AC交AC的延长线上于点E,延长线段AB、ED交于点F,连接DA、DB.
(1)求证:DE是⊙O的切线;
(2)若AB=10,,求BF.
23.(本小题满分10分)
为推进全民健身设施建设,某体育中心准备改扩建一块运动场地.现有甲、乙两个工程队参与施工,具体信息如下:
信息一
工程队 每天施工面积(单位:m2) 每天施工费用(单位:元)
甲 x+300 3600
乙 x 2200
信息二
甲工程队施工1800m2所需天数与乙工程队施工1200m2所需天数相等.
(1)求x的值;
(2)该工程计划先由甲工程队单独施工若干天,再由乙工程队单独继续施工,两队共施工22天,且完成的施工面积不少于15000m2.该段时间内体育中心至少需要支付多少施工费用?
24.(本小题满分10分)
阅读与思考:下面是小亮同学的一篇数学日记,请仔细阅读并完成相应的任务.
今天是2023年12月4日(星期一),在下午数学活动课上,我们“腾飞”小组的同学参加了人教九年级下册19页“活动2”的探究活动.如图,取一根长100cm的匀质木杆,用细绳绑在木杆的中点O并将其吊起来,在中点O的左侧距离中点O25cm处挂一个重9.8N的物体,在中点O右侧用一个弹簧秤向下拉,使木杆处于水平状态,改变弹簧秤与中点O的距离l(单位:cm),看弹簧秤的示数F(单位,N)有什么变化.第一步,实验测量.改变弹簧秤与中点O的距离L,观察弹簧秤的示数F的值,并做好记录(共记录了7组数据).第二步,整理数据.第一组第二组第三组第四组第五组第六组第七组L/cm…5101420253540…F/N…4924.517.512.259.886.125…第三步,描点连线.以L的数值为横坐标,对应F的数值为纵坐标在平面直角坐标系中描出以表中数对为坐标的各点,并用平滑的曲线顺次连接这些点.在数据分析时,我发现一个数据有错误,重新测量计算后,证明了我的猜想正确,并修改了表中这个数据.实验结束后,大家都有很多收获,每人都撰写了日记.
任务:(1)你认为表中第几组数据是错误的?请把这组数据改正过来:
(2)在平面直角坐标系中,画出F与L的函数图象:
(3)这条曲线是反比例函数的一支吗?为什么?并直接写出F关于L的函数表达式;
(4)点(50,4.9)在这条曲线上吗?说明理由.
25.(本小题满分12分)
如图1,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0)与y轴交于点C.
(1)求抛物线的函数表达式.
(2)如图2,当点P从点B匀速运动到点O时,过点P作PF⊥AB交抛物线于点F,交直线BC于点E,连结CF.求S△CBF的最大值.
(3)若点P从点B匀速运动到点A时,点Q恰好从点C运动到点O,作点Q关于直线BC的对称点Q',当点Q'落在△CEF的一条边上时,请直接写出CQ的长度.
26.(本小题满分12分)
综合与实践:
问题背景:借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究.
如图1,在△ABC中,∠B=90°,AB=BC=4,分别取AB,AC的中点D,E,作△ADE.如图2所示,将△ADE绕点A逆时针旋转,连结BD,CE.
(1)探究发现
旋转过程中,线段BD和CE的长度存在怎样的数量关系?写出你的猜想,并证明.
(2)性质应用
如图3,当DE所在直线首次经过点B时,求CE的长.
(3)延伸思考
如图4,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,分别取AB,BC的中点D,E、作△BDE.将△BDE绕点B逆时针旋转,连接AD,CE.当边AB平分线段DE时,求tan∠ECB的值.
济南市2024年九年级学业水平考试
数学综合试题模拟参考答案
一、选择题(本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂写在答题卡上,每小题选对得4分,选错、不选或选出的答案超过一个均记0分,共40分)
1.B 2.B 3.D 4.A 5.B 6.D 7.D 8.B 9.C 10.D
二、填空题(本大题共6个小题,每小题4分,共24分.请直接写答案.)
11.(m﹣6)(m+6) 12. 13.2024
14.2.6 15.2 16.(3,﹣1)
三、解答题(本大题共10小题,共86分,解答应写出文字说明,证明过程或演算步骤.)
17.解:原式=11+22.
18.解:,
解不等式①得,x≤2,
解不等式②得,x>﹣1,
∴不等式组的解集是﹣1<x≤2,
在数轴上表示为
,
∴不等式组的整数解是:0,1,2.
19.解:四边形AECF是矩形,
理由:∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠D=∠B,
∵AF=CE,
∴AD﹣AF=CB﹣CE,
∴DF=BE,
在△CDF和△ABE中,
,
∴△CDF和≌△ABE(SAS),
∴CF=AE,
∴四边形AECF是平行四边形,
∵作CF⊥AD于点F,
∴∠AFC=90°,
∴四边形AECF是矩形.
20.解:(1)在Rt△DCE中,DE=70厘米,∠CED=57°,
∵cos∠CED,
∴CE=DE cos∠CED≈70×0.6=42(厘米),
答:支架CE的长度约为42厘米;
(2)设水箱半径的长度为x厘米,
在Rt△DCE中,DE=70厘米,∠CED=57°,
∵sin∠CED,
∴CD=DE sin∠CED≈70×0.8=56(厘米),
∵斜面AB坡度为1:,
∴tanA,
∴∠A=30°,
∵sinA,
∴,
解得:x=19,
经检验,x=19是原方程的根,
答:水箱半径的长度约为19厘米.
21.解:(1)50,7;
(2)由(1)知,m=7,
等级为A的有:50﹣16﹣15﹣7=12(人),
补充完整的条形统计图如图所示,
C等所在扇形圆心角的度数为:360°108°;
(3)1000×(24%+32%)
=1000×56%
=560(人),
即估计该校学生答题成绩良好以上的有560人;
(4)树状图如下所示:
由上可得,一共存在12种等可能性,其中抽出的两名学生恰好都是男生的可能性有2种,
∴抽出的两名学生恰好都是男生的概率为.
22.(1)证明:连接OD,
∵∠BAC 的角平分线与⊙O 交于点D,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴AC∥DO,
∵DE⊥AC,
∴∠E=90°,
∴∠ODF=∠E=90°,
∴OD⊥DE,
∵OD是⊙O的半径,OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=10,,
∴BD2,
过点D作 DM⊥AB于点M,
∵S△ABD,
∴DM4,
∴AM8,
设BF=x,
∵∠BAC 的角平分线与⊙O 交于点D,DE⊥AC,DM⊥AB,
∴DE=DM,
∴CD=BD,
在Rt△AED和Rt△AMD中,
,
Rt△AED≌Rt△AMD(HL),
∴AE=AM,
∵DM=4,
∴DE=DM=4,
∵AM=8
∴AE=AM=8,
∵∠F=∠F,∠ODF=∠E=90°,
∴△FDO∽△FEA,
∴,
∴,
∴x,
∴BF.
23.解:(1)根据题意得:,
解得:x=600,
经检验,x=600是所列方程的解,且符合题意.
答:x的值为600;
(2)设甲工程队施工m天,则乙工程队单独施工(22﹣m)天,
根据题意得:(600+300)m+600(22﹣m)≥15000,
解得:m≥6,
设该段时间内体育中心需要支付w元施工费用,则w=3600m+2200(22﹣m),
即w=1400m+48400,
∵1400>0,
∴w随m的增大而增大,
∴当m=6时,w取得最小值,最小值=1400×6+48400=56800.
答:该段时间内体育中心至少需要支付56800元施工费用.
24.解:(1)根据表中数据,可发现L与F的乘积为定值245,
所以第六组数据是错误的,
正确应该是:L=35时,F=7;
(2)画出F与L的函数图象如图:
(3)因为F、L都是正数,
所以这条曲线是反比例函数的一支,
因为 FL=245,
其函数表达式为:F;
(4)因为50×4.9=245,
∴点(50,4.9)在这条曲线上.
25.解:(1)将点A(﹣1,0),B(3,0)代入y=﹣x2+bx+c,
得,
解得,
∴抛物线的函数表达式为y=﹣x2+2x+3;
(2)把x=0代入y=﹣x2+2x+3,得y=3,
∴点C的坐标为(0,3),
设直线BC的解析式为y=kx+b,
把B(3,0),C(0,3)代入,
得,
解得,
∴直线BC的解析式为y=﹣x+3,
设点P的坐标为(m,0),
由过点P作PF⊥AB交抛物线于点F,交直线BC于点E,得E(m,﹣m+3),F(m,﹣m2+2m+3),
由点P从点B匀速运动到点,得点E和F均在第一象限,
∴EF=(﹣m2+2m+3)﹣(﹣m+3)=﹣m2+3m(0<m<3),
当时,EF取得最大值,
∵S△CBF=S△CEF+S△BEF,
∴S△CBF的最大值为;
(3).
26.解:(1)CE,理由如下:
∵∠B=90°,AB=BC,
∴ACAB,
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
∵,
∴△ABD∽△ACE,
∴,
∴CE;
(2)由(1)知:△ABD∽△ACE,
∴∠ABE=∠ACE,∠ADE=∠AEC,∠ADB=∠AEC,
∴点A、B、C、E共圆,
∴∠AEC+∠ABC=180°,∠BCE=∠BAC=45°,
∵∠ABC=90°,
∴∠ADB=∠AEC=90°,
∴∠AEB=45°,
∵AB=4,AD=2,
∴AEAD=2,
∴CE2;
(3)如图,
设AB与DE相交于点Q,作EF⊥BC于F,
∵△DBE∽△ABC,
∴∠BED=∠ACB,∠DBE=∠ABC=90°,
∵AB平分DE,
∴DQ=QE,
∴BQ=EQQE,
∴∠ABE=∠DEB=∠ACB,
∵∠ABE+∠CBE=90°,∠CBE+∠BEG=90°,
∴∠ABE=∠BEG,
∴∠BEG=∠ACB,
∴BG=BE sin∠BEG=3 sin∠ACB=3,
EG=BE cos∠BEG=3,
∴CG=BC﹣BG=6,
∴tan∠ECB.
同课章节目录
