18.1.2平行四边形的判定 课件(共28张PPT)
文档属性
| 名称 | 18.1.2平行四边形的判定 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 17:03:11 | ||
图片预览





文档简介
(共28张PPT)
18.1.3 平行四边形的判定
八年级下
人教版
1.探索并证明平行四边形的判定定理.
2.能熟练运用平行四边形的判定定理去计算和证明.
学习目标
重点
难点
平行四边形的性质有哪些?
平行四边形的对边相等,对角相等,对角线互相平分.
该怎样判定一个四边形是平行四边形呢?
新课引入
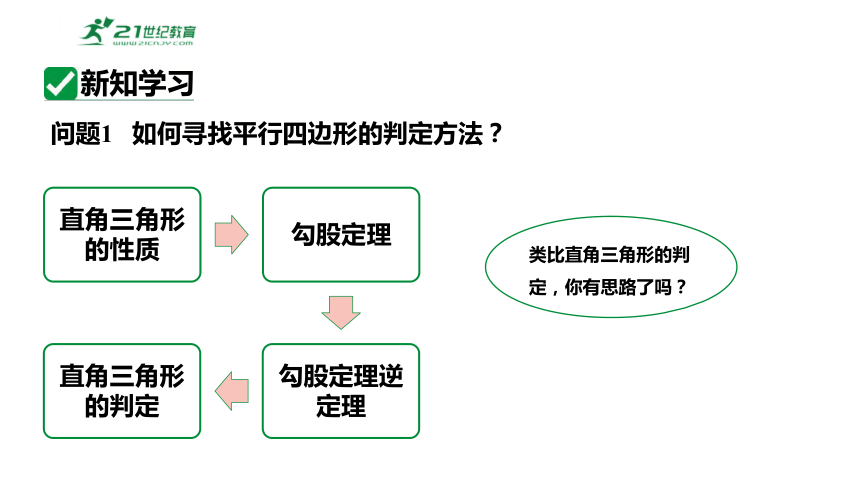
问题1 如何寻找平行四边形的判定方法?
类比直角三角形的判定,你有思路了吗?
新知学习
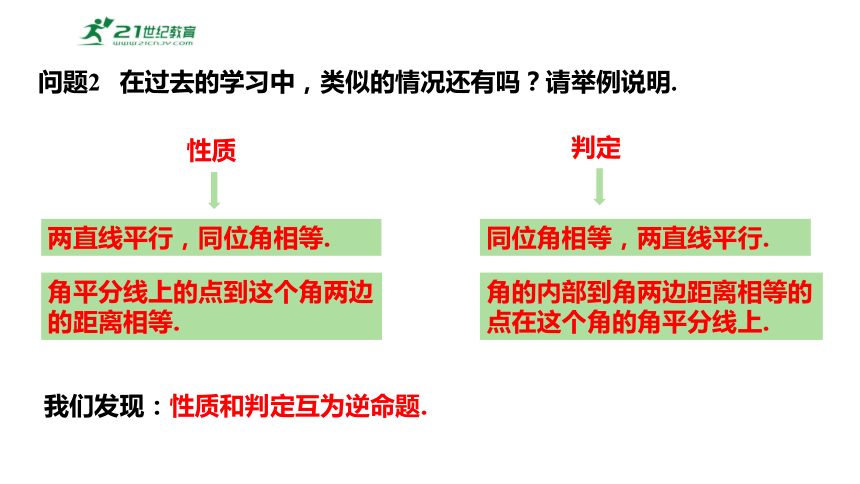
问题2 在过去的学习中,类似的情况还有吗?请举例说明.
两直线平行,同位角相等.
同位角相等,两直线平行.
角平分线上的点到这个角两边的距离相等.
角的内部到角两边距离相等的点在这个角的角平分线上.
我们发现:性质和判定互为逆命题.
性质
判定
平行四边形的性质 猜 想 (判 定)
对边相等
对角相等
对角线互相平分
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
逆向思考,提出猜想:
这些猜想正确吗?
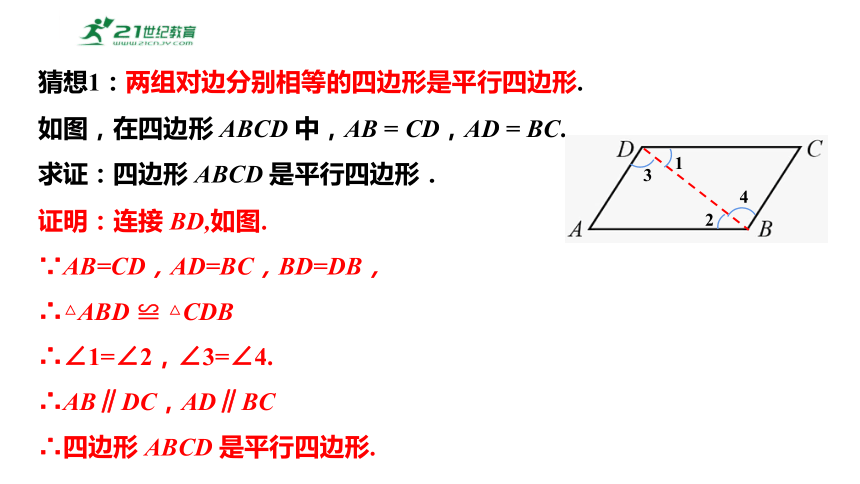
猜想1:两组对边分别相等的四边形是平行四边形.
如图,在四边形 ABCD 中,AB = CD,AD = BC.
求证:四边形 ABCD 是平行四边形.
证明:连接 BD,如图.
∵AB=CD,AD=BC,BD=DB,
∴△ABD ≌ △CDB
∴∠1=∠2,∠3=∠4.
∴AB∥DC,AD∥BC
∴四边形 ABCD 是平行四边形.
1
2
3
4
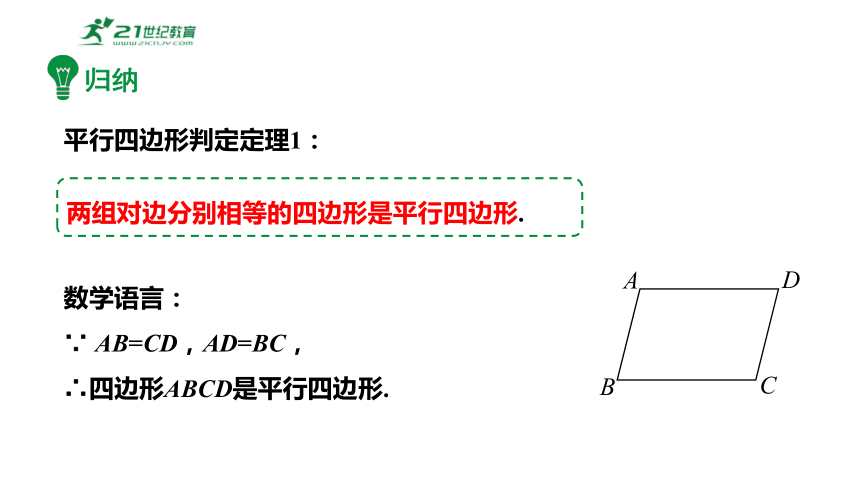
归纳
两组对边分别相等的四边形是平行四边形.
平行四边形判定定理1:
A
B
C
D
数学语言:
∵ AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
猜想2:两组对角分别相等的四边形是平行四边形.
如图,在四边形 ABCD 中,∠A = ∠C,∠B = ∠D.
求证:四边形 ABCD 是平行四边形.
证明:∵∠A + ∠B + ∠C + ∠D = 360°.
∠A = ∠C,∠B = ∠D,
∴∠A + ∠B = 180°,∠B + ∠C = 180°.
∴AD∥BC,AB∥DC.
∴四边形 ABCD 是平行四边形.
归纳
两组对角分别相等的四边形是平行四边形.
平行四边形判定定理2:
A
B
C
D
数学语言:
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
猜想3:对角线互相平分的四边形是平行四边形.
如图,在四边形 ABCD 中,AC,BD 相交于点 O,且 OA = OC,OB = OD. 求证:四边形 ABCD 是平行四边形.
证明:∵ OA = OC,OB = OD,
∠AOD = ∠COB
∴△AOD ≌ △COB
∴∠OAD = ∠OCB.
∴AD∥BC
同理 AB∥DC.
∴四边形 ABCD 是平行四边形.
归纳
对角线互相平分的四边形是平行四边形.
平行四边形判定定理3:
数学语言:
A
B
C
D
O
∵ OA=OC , OB=OD,
∴ 四边形ABCD是平行四边形.
由上我们知道,平行四边形的判定定理与相应的性质定理互为逆定理.也就是说,当定理的条件与结论互换以后,所得命题仍然成立.
这张图揭示了定义、性质、判定间的逻辑关系,提供了研究几何图形的一般思路.
例1 如图,□ABCD 的对角线 AC,BD 相交于点 O,E,F是 AC上的两点,并且 AE=CF. 求证:四边形 BFDE 是平行四边形.
A
B
C
D
O
E
F
分析:点E,F在平行四边形的对角线上,可考虑利用对角线互相平分来证明四边形BFDE是平行四边形.
证明:∵ 四边形 ABCD 是平行四边形,
∴ AO=CO, BO=DO.
∵ AE=CF,
∴ AO-AE=CO-CF, 即EO=FO.
又 BO=DO,
∴ 四边形BFDE是平行四边形.
A
B
C
D
O
E
F
变式 如图,□ABCD 的对角线 AC,BD 相交于点 O,点 E,F 分别在 AC 两侧的延长线上,且 AE=CF. 求证:四边形 BFDE 是平行四边形.
O
证明:∵四边形 ABCD 是平行四边形,
∴OA = OC,OB = OD,
∵AE = CF,OE = AO + AE,OF = OC + CF,
∴OE = OF,
又∵OB = OD,
∴四边形 BFDE 是平行四边形.
思考
我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢
猜想:一组对边平行且相等的四边形是平行四边形.
我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗
如图,在四边形 ABCD 中,AB = DC,AB∥DC.
求证:四边形 ABCD 是平行四边形.
证明:连接 AC,如图.
∵AB∥DC ∴∠1 = ∠2,
又 AB = DC,AC = AC
∴△ABC ≌△CDA
∴AD = BC
∴四边形 ABCD 的两组对边分别相等,它是平行四边形.
猜想:一组对边平行且相等的四边形是平行四边形.
A
B
C
D
1
2
归纳
一组对边平行且相等的四边形是平行四边形.
平行四边形判定定理4:
A
B
C
D
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形.
数学语言:
归纳
平行四边形的判定方法:
1. 定义:两组对边分别平行的四边形叫做平行四边形.
2. 判定定理:
(1) 两组对边分别相等的四边形是平行四边形.
(2) 两组对角分别相等的四边形是平行四边形.
(3) 对角线互相平分的四边形是平行四边形.
(4) 一组对边平行且相等的四边形是平行四边形.
例2 如图,在 □ABCD 中,E,F 分别是 AB,CD 的中点.
求证:四边形 EBFD 是平行四边形.
证明:∵四边形 ABCD 是平行四边形,
∴AB = CD,DF //EB,
又 DF = DC,EB = AB.
∴DF = EB,
∴四边形 EBFD 是平行四边形.
随堂练习
1. 如图是乐乐家中的鞋架及其侧面简易图,若AB=CD,AF=CE,∠B=∠D=90°,∠BAE=∠DCF.求证:四边形AECF为平行四边形.
第1题图
例 证明:在△ABE和△CDF中,
∴△ABE≌△CDF(ASA),
∴AE=CF,
又∵AF=CE,
∴四边形AECF为平行四边形.
第1题图
2.如图,已知在平行四边形ABCD中,AE,CF分别是∠DAB,∠BCD的平分线. 求证:四边形AFCE是平行四边形.
D
C
B
A
E
F
分析:已知AF∥CE,利用定义法来证明FC∥AE 进而证明平行四边形;也可通过两组对角分别相等来证明平行四边形.
又∵ AE,CF分别是∠DAB,∠BCD的平分线,
∴∠DAE=∠BAE=∠DCF=∠BCF.
证明:∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴四边形AFCE是平行四边形.
∵AD∥BC,
∴ ∠DFC=∠FCB,∠DAE=∠AEB,
∴ ∠AFC=∠AEC,
D
C
B
A
E
F
3.如图,分别以 Rt△ABC 的直角边 AC 及斜边 AB 向外作等边△ACD、等边△ABE. 且∠BAC = 30°,EF⊥AB,垂足为 F,连接 DF.
(1) 试说明 AC = EF;
解:(1) 在 Rt△ABC 中,∠BAC = 30°,∴BC = AB,
∵△ABE 是等边三角形,EF⊥AB,
∴AF = AB,∴BC = AF,
∵△ABE 是等边三角形,
∴AB = AE,∴Rt△FEA ≌ Rt△CAB (HL),
∴AC = EF.
(2) 求证:四边形 ADFE 是平行四边形.
证明:∵△ACD 是等边三角形,∴∠DAC = 60°,
∵∠BAC = 30°. ∴∠BAD = 90°,
∵EF⊥AB,∴∠AFE = 90°.
∴∠BAD = ∠AFE,
∴AD∥EF,
∵△ACD 是等边三角形,AC = AD,
∵AC = EF,∴AD = EF.
∴四边形 ADFE 是平行四边形.
判定一个四边形是平行四边形可从哪些角度思考?
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
从边考虑
从角考虑
从对角线考虑
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
课堂小结
18.1.3 平行四边形的判定
八年级下
人教版
1.探索并证明平行四边形的判定定理.
2.能熟练运用平行四边形的判定定理去计算和证明.
学习目标
重点
难点
平行四边形的性质有哪些?
平行四边形的对边相等,对角相等,对角线互相平分.
该怎样判定一个四边形是平行四边形呢?
新课引入
问题1 如何寻找平行四边形的判定方法?
类比直角三角形的判定,你有思路了吗?
新知学习
问题2 在过去的学习中,类似的情况还有吗?请举例说明.
两直线平行,同位角相等.
同位角相等,两直线平行.
角平分线上的点到这个角两边的距离相等.
角的内部到角两边距离相等的点在这个角的角平分线上.
我们发现:性质和判定互为逆命题.
性质
判定
平行四边形的性质 猜 想 (判 定)
对边相等
对角相等
对角线互相平分
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
逆向思考,提出猜想:
这些猜想正确吗?
猜想1:两组对边分别相等的四边形是平行四边形.
如图,在四边形 ABCD 中,AB = CD,AD = BC.
求证:四边形 ABCD 是平行四边形.
证明:连接 BD,如图.
∵AB=CD,AD=BC,BD=DB,
∴△ABD ≌ △CDB
∴∠1=∠2,∠3=∠4.
∴AB∥DC,AD∥BC
∴四边形 ABCD 是平行四边形.
1
2
3
4
归纳
两组对边分别相等的四边形是平行四边形.
平行四边形判定定理1:
A
B
C
D
数学语言:
∵ AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
猜想2:两组对角分别相等的四边形是平行四边形.
如图,在四边形 ABCD 中,∠A = ∠C,∠B = ∠D.
求证:四边形 ABCD 是平行四边形.
证明:∵∠A + ∠B + ∠C + ∠D = 360°.
∠A = ∠C,∠B = ∠D,
∴∠A + ∠B = 180°,∠B + ∠C = 180°.
∴AD∥BC,AB∥DC.
∴四边形 ABCD 是平行四边形.
归纳
两组对角分别相等的四边形是平行四边形.
平行四边形判定定理2:
A
B
C
D
数学语言:
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
猜想3:对角线互相平分的四边形是平行四边形.
如图,在四边形 ABCD 中,AC,BD 相交于点 O,且 OA = OC,OB = OD. 求证:四边形 ABCD 是平行四边形.
证明:∵ OA = OC,OB = OD,
∠AOD = ∠COB
∴△AOD ≌ △COB
∴∠OAD = ∠OCB.
∴AD∥BC
同理 AB∥DC.
∴四边形 ABCD 是平行四边形.
归纳
对角线互相平分的四边形是平行四边形.
平行四边形判定定理3:
数学语言:
A
B
C
D
O
∵ OA=OC , OB=OD,
∴ 四边形ABCD是平行四边形.
由上我们知道,平行四边形的判定定理与相应的性质定理互为逆定理.也就是说,当定理的条件与结论互换以后,所得命题仍然成立.
这张图揭示了定义、性质、判定间的逻辑关系,提供了研究几何图形的一般思路.
例1 如图,□ABCD 的对角线 AC,BD 相交于点 O,E,F是 AC上的两点,并且 AE=CF. 求证:四边形 BFDE 是平行四边形.
A
B
C
D
O
E
F
分析:点E,F在平行四边形的对角线上,可考虑利用对角线互相平分来证明四边形BFDE是平行四边形.
证明:∵ 四边形 ABCD 是平行四边形,
∴ AO=CO, BO=DO.
∵ AE=CF,
∴ AO-AE=CO-CF, 即EO=FO.
又 BO=DO,
∴ 四边形BFDE是平行四边形.
A
B
C
D
O
E
F
变式 如图,□ABCD 的对角线 AC,BD 相交于点 O,点 E,F 分别在 AC 两侧的延长线上,且 AE=CF. 求证:四边形 BFDE 是平行四边形.
O
证明:∵四边形 ABCD 是平行四边形,
∴OA = OC,OB = OD,
∵AE = CF,OE = AO + AE,OF = OC + CF,
∴OE = OF,
又∵OB = OD,
∴四边形 BFDE 是平行四边形.
思考
我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢
猜想:一组对边平行且相等的四边形是平行四边形.
我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗
如图,在四边形 ABCD 中,AB = DC,AB∥DC.
求证:四边形 ABCD 是平行四边形.
证明:连接 AC,如图.
∵AB∥DC ∴∠1 = ∠2,
又 AB = DC,AC = AC
∴△ABC ≌△CDA
∴AD = BC
∴四边形 ABCD 的两组对边分别相等,它是平行四边形.
猜想:一组对边平行且相等的四边形是平行四边形.
A
B
C
D
1
2
归纳
一组对边平行且相等的四边形是平行四边形.
平行四边形判定定理4:
A
B
C
D
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形.
数学语言:
归纳
平行四边形的判定方法:
1. 定义:两组对边分别平行的四边形叫做平行四边形.
2. 判定定理:
(1) 两组对边分别相等的四边形是平行四边形.
(2) 两组对角分别相等的四边形是平行四边形.
(3) 对角线互相平分的四边形是平行四边形.
(4) 一组对边平行且相等的四边形是平行四边形.
例2 如图,在 □ABCD 中,E,F 分别是 AB,CD 的中点.
求证:四边形 EBFD 是平行四边形.
证明:∵四边形 ABCD 是平行四边形,
∴AB = CD,DF //EB,
又 DF = DC,EB = AB.
∴DF = EB,
∴四边形 EBFD 是平行四边形.
随堂练习
1. 如图是乐乐家中的鞋架及其侧面简易图,若AB=CD,AF=CE,∠B=∠D=90°,∠BAE=∠DCF.求证:四边形AECF为平行四边形.
第1题图
例 证明:在△ABE和△CDF中,
∴△ABE≌△CDF(ASA),
∴AE=CF,
又∵AF=CE,
∴四边形AECF为平行四边形.
第1题图
2.如图,已知在平行四边形ABCD中,AE,CF分别是∠DAB,∠BCD的平分线. 求证:四边形AFCE是平行四边形.
D
C
B
A
E
F
分析:已知AF∥CE,利用定义法来证明FC∥AE 进而证明平行四边形;也可通过两组对角分别相等来证明平行四边形.
又∵ AE,CF分别是∠DAB,∠BCD的平分线,
∴∠DAE=∠BAE=∠DCF=∠BCF.
证明:∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴四边形AFCE是平行四边形.
∵AD∥BC,
∴ ∠DFC=∠FCB,∠DAE=∠AEB,
∴ ∠AFC=∠AEC,
D
C
B
A
E
F
3.如图,分别以 Rt△ABC 的直角边 AC 及斜边 AB 向外作等边△ACD、等边△ABE. 且∠BAC = 30°,EF⊥AB,垂足为 F,连接 DF.
(1) 试说明 AC = EF;
解:(1) 在 Rt△ABC 中,∠BAC = 30°,∴BC = AB,
∵△ABE 是等边三角形,EF⊥AB,
∴AF = AB,∴BC = AF,
∵△ABE 是等边三角形,
∴AB = AE,∴Rt△FEA ≌ Rt△CAB (HL),
∴AC = EF.
(2) 求证:四边形 ADFE 是平行四边形.
证明:∵△ACD 是等边三角形,∴∠DAC = 60°,
∵∠BAC = 30°. ∴∠BAD = 90°,
∵EF⊥AB,∴∠AFE = 90°.
∴∠BAD = ∠AFE,
∴AD∥EF,
∵△ACD 是等边三角形,AC = AD,
∵AC = EF,∴AD = EF.
∴四边形 ADFE 是平行四边形.
判定一个四边形是平行四边形可从哪些角度思考?
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
从边考虑
从角考虑
从对角线考虑
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
课堂小结
