18.2.3正方形 课件(共33张PPT)
文档属性
| 名称 | 18.2.3正方形 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 00:00:00 | ||
图片预览




文档简介
(共33张PPT)
18.2.3 正方形
八年级下
人教版
1. 理解正方形的概念,以及它与平行四边形、矩形、菱形之间的关系;
2. 能熟练运用正方形的性质和判定进行计算和证明.
学习目标
重点
难点
新课引入
正方形是我们熟悉的几何图形,它的边、角有什么特点?
正方形的四条边都相等,四个角都是直角.
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
两层含义
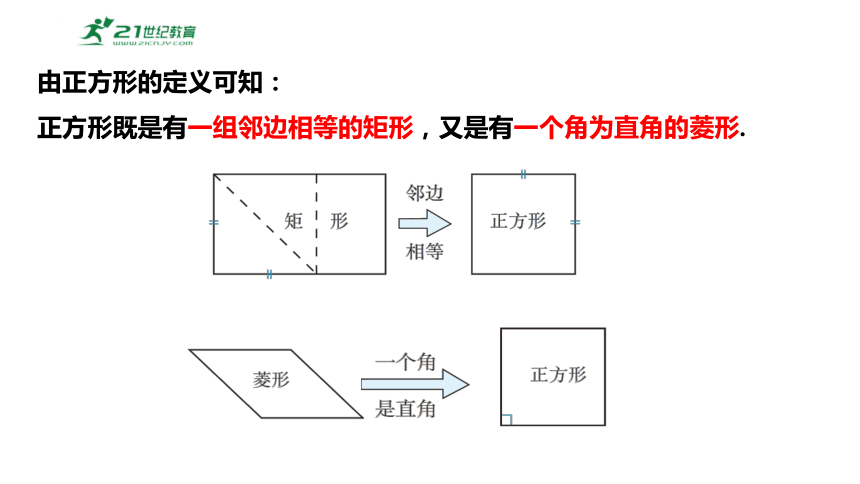
(1) 有一组邻边相等的平行四边形 (菱形)
(2) 并且有一个角是直角的平行四边形 (矩形)
新知学习
一 正方形的定义及其性质
由正方形的定义可知:
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.
思考
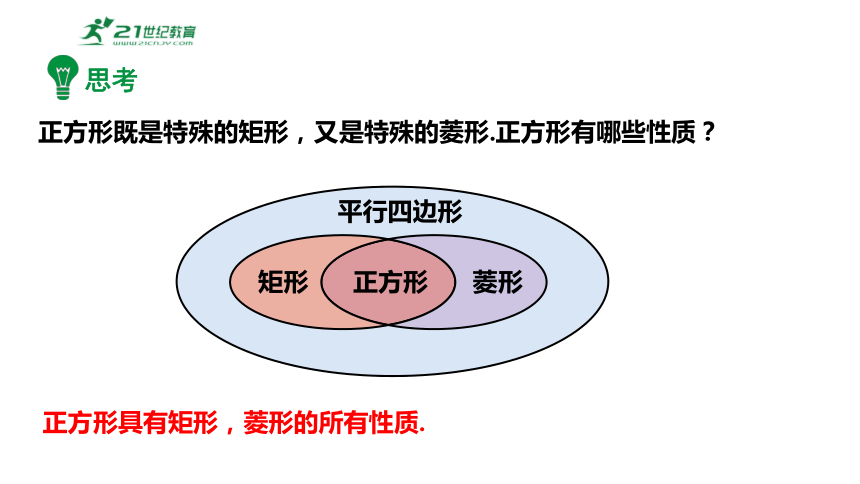
正方形既是特殊的矩形,又是特殊的菱形.正方形有哪些性质?
正方形具有矩形,菱形的所有性质.
平行四边形
矩形
菱形
正方形
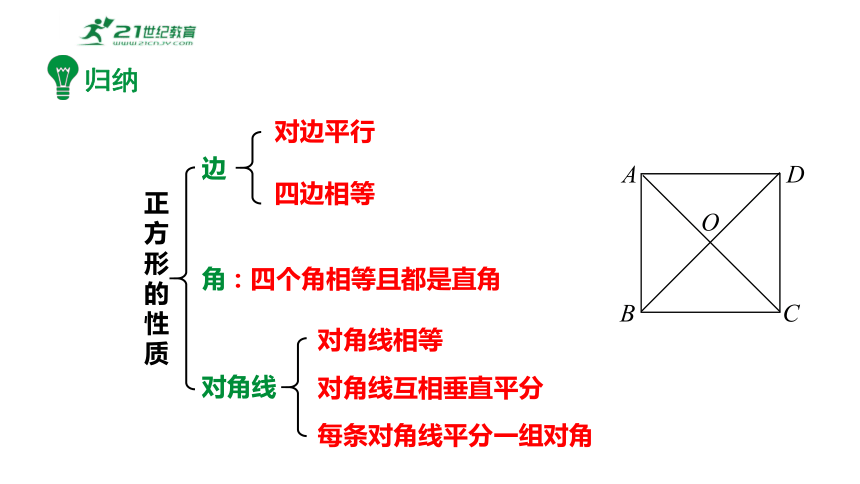
归纳
正方形的性质
边
对边平行
四边相等
角
对角线
对角线相等
对角线互相垂直平分
每条对角线平分一组对角
:四个角相等且都是直角
A
B
D
C
O
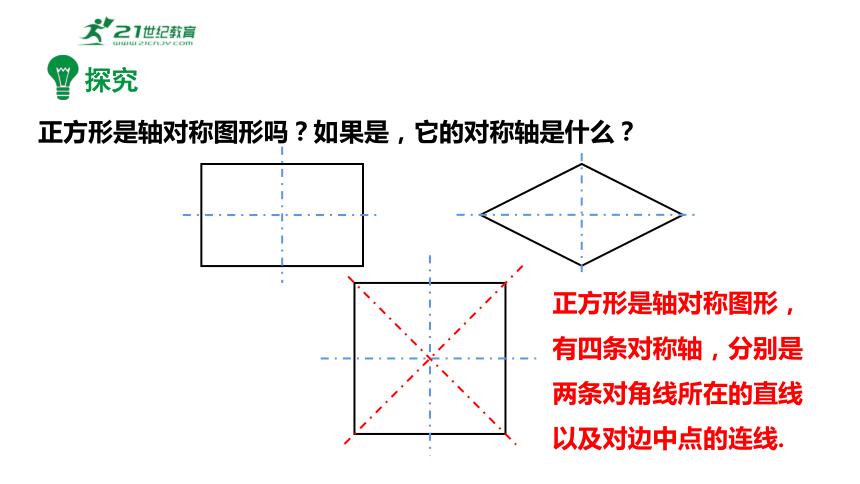
探究
正方形是轴对称图形吗?如果是,它的对称轴是什么?
正方形是轴对称图形,有四条对称轴,分别是两条对角线所在的直线以及对边中点的连线.
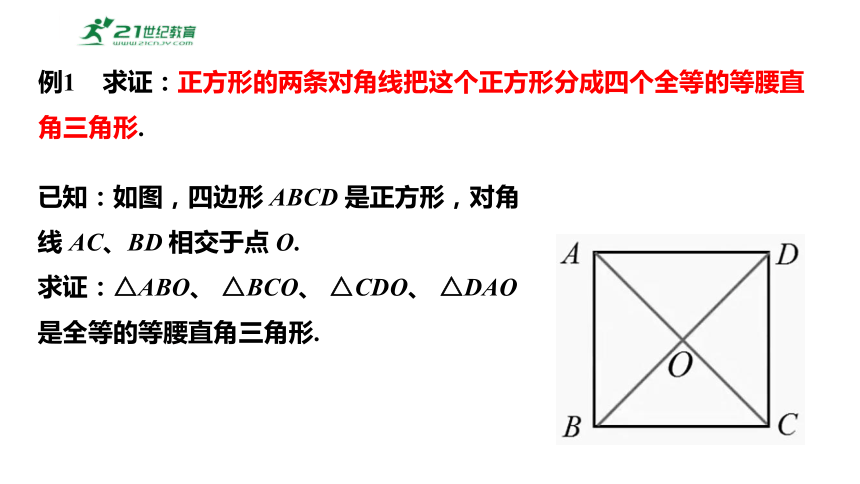
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形 ABCD 是正方形,对角线 AC、BD 相交于点 O.
求证:△ABO、 △BCO、 △CDO、 △DAO 是全等的等腰直角三角形.
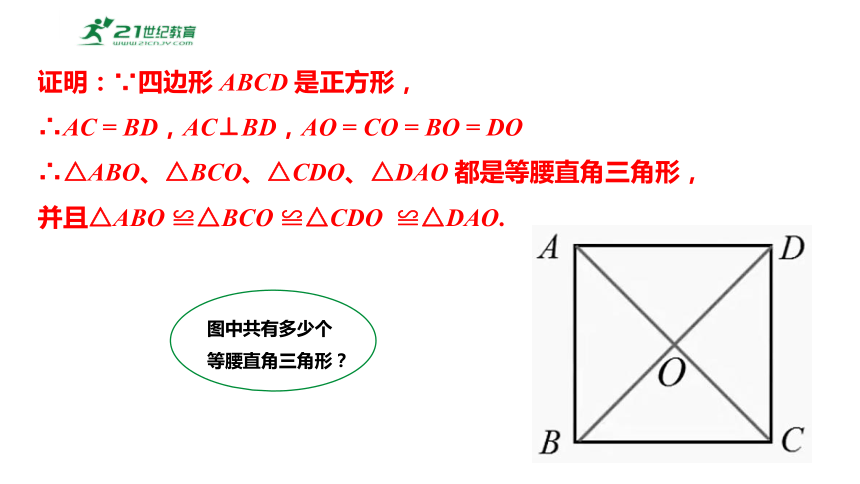
证明:∵四边形 ABCD 是正方形,
∴AC = BD,AC⊥BD,AO = CO = BO = DO
∴△ABO、△BCO、△CDO、△DAO 都是等腰直角三角形,
并且△ABO ≌△BCO ≌△CDO ≌△DAO.
图中共有多少个等腰直角三角形?
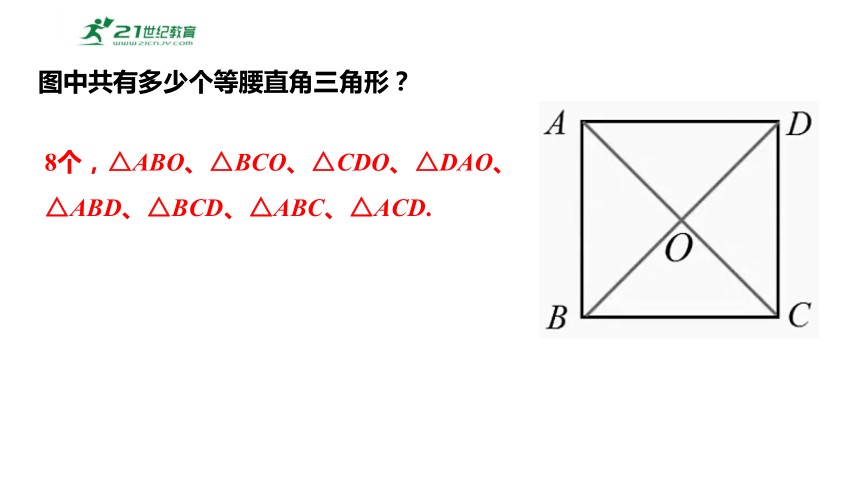
图中共有多少个等腰直角三角形?
8个,△ABO、△BCO、△CDO、△DAO、△ABD、△BCD、△ABC、△ACD.
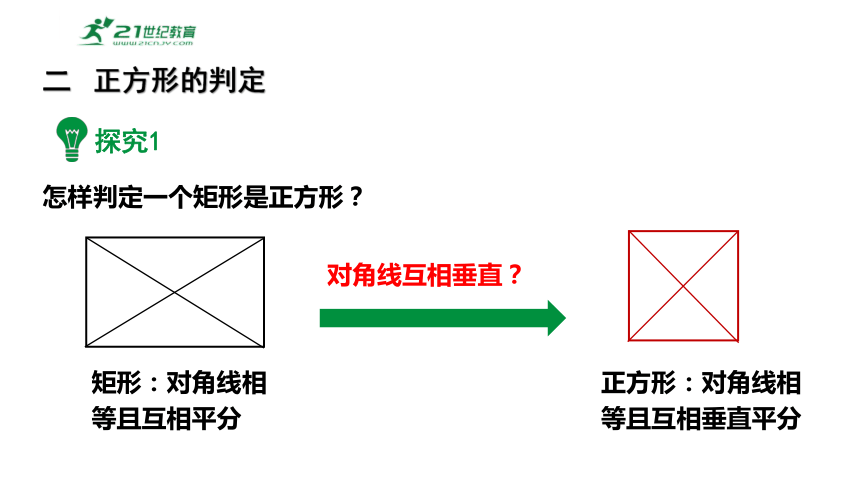
探究1
怎样判定一个矩形是正方形?
二 正方形的判定
矩形:对角线相等且互相平分
正方形:对角线相等且互相垂直平分
对角线互相垂直?
已知:在矩形ABCD中,AC⊥BD.
求证:四边形ABCD是正方形.
证明: ∵四边形ABCD是矩形,
A
B
D
C
O
∴OA=OB=OC=OD,∠BAD=90 .
∵AC⊥BD,
∴AC是线段BD的垂直平分线.
∴AB=BC=CD=DA,
∴四边形ABCD是正方形.
同理:BD是线段AC的垂直平分线,
数学语言:
在矩形ABCD中, ∵ AC⊥BD,
∴四边形ABCD是正方形.
A
B
D
C
O
归纳
对角线互相垂直的矩形是正方形.
通过以上证明,我们得到正方形的一个判定:
探究2
怎样判定一个矩形是正方形?
矩形:对边相等
且平行
正方形:四边相等且对边平行
邻边相等?
已知:在矩形ABCD中,AB=BC.
求证:四边形ABCD是正方形.
证明: ∵四边形ABCD是矩形,
A
B
D
C
∴∠B=90 ,四边形ABCD是平行四边形.
∵AB=BC,
∴四边形ABCD是正方形.
归纳
有一组邻边相等的矩形是正方形.
通过以上证明,我们得到正方形的一个判定:
数学语言:
在矩形ABCD中, ∵AB=BC,
∴四边形ABCD是正方形.
A
B
D
C
O
探究3
怎样判定一个菱形是正方形?
菱形:对角线垂直且互相平分
正方形:对角线相等且互相垂直平分
对角线相等?
已知:在菱形ABCD中,AC,BD是两条对角线,且 AC=BD.
求证:四边形ABCD是正方形.
证明: ∵四边形ABCD是菱形,
A
B
D
C
O
∴AB=BC=CD=DA,AC⊥BD.
∵AC=BD,
∴OA=OB=OC=OD,
∴△AOB ,△BOC是等腰直角三角形,
∴四边形ABCD是正方形.
∴∠ABC=90 ,
归纳
对角线相等的菱形是正方形.
通过以上证明,我们得到正方形的一个判定:
数学语言:
在菱形ABCD中, ∵ AC=BD,
∴四边形ABCD是正方形.
A
B
D
C
O
探究4
怎样判定一个菱形是正方形?
菱形:对角相等
正方形:四个角相等,都为90°
有一个角为直角?
已知:在菱形ABCD中,∠A=90 .
求证:四边形ABCD是正方形.
证明: ∵四边形ABCD是菱形,
A
B
D
C
∴AB=BC=CD=DA,
四边形ABCD是平行四边形,
∵∠A=90 ,
∴四边形ABCD是正方形.
归纳
有一个角是直角的菱形是正方形.
通过以上证明,我们得到正方形的一个判定:
数学语言:
在菱形ABCD中,∵ ∠A=90 ,
∴四边形ABCD是正方形.
A
B
D
C
O
一个角是直角
或对角线相等
一组邻边相等
或对角线相互垂直
一组邻边相等
或对角线相互垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
对角线相等且互相垂直
归纳
例2 下列各句判定正方形的说法是否正确?
(1) 有一个角是直角的菱形是正方形. ( )
(2) 有一组邻边相等的矩形是正方形. ( )
(3) 对角线相等的菱形是正方形. ( )
(4) 对角线互相垂直的矩形是正方形. ( )
(5) 对角线相等且互相垂直的四边形是正方形. ( )
√
√
√
√
×
对角线相等且互相垂直平分的四边形是正方形.
或者对角线相等且互相垂直的平行四边形是正方形.
随堂练习
B
A.对角线互相垂直平分
B.对角线相等
C.对角线平分一组对角
D.四边相等
1.正方形具有而菱形不具有的性质是( ).
D
A.对角互补
B.对角线相等
C.四个角相等
D.对角线互相垂直
2.正方形具有而矩形不具有的性质是( ).
3.在正方形 ABCD 中,AB = 12 cm,对角线 AC、BD 相交于 O,则△ABO 的周长是 (____________) cm.
分析:△ABO 是等腰直角三角形,AB = 12 cm,
利用勾股定理,可以求出 OA = OB = cm,
所以△ABO 的周长是 ( ) cm.
3.如图,四边形ABCD是一块正方形场地.小华和小芳在AB边上取定了一点 E,测量知,EC=30m,EB=10m. 这块场地的面积和对角线分别是多少?
∴在Rt△EBC中
m.
解:∵四边形ABCD是正方形, ∴∠B=90 .
∴AB=BC=CD=DA=m,
∴场地的面积为,
对角线的长为
4.如图,正方形 ABCD,直线l1过点A,直线l2过点C,且l1∥l2,过点D作PN⊥l1垂足为N,交l2于点P,过点B作QM⊥l1垂足为M,交l2于点Q.
求证:四边形PNMQ是正方形.
证明:PN⊥l1,QM⊥l1,
∴PN∥QM,∠PNM =∠QMN = 90°.
∵l1∥l2,即 PQ∥NM,
∴四边形 PQMN 是矩形.
∵四边形 ABCD 是正方形,
∴∠BAD =90°,AB = AD ,
∴∠BAM +∠DAN = 90°.
又∠ADN +∠DAN = 90°,
∴∠BAM =∠ADN.
∴△BAM ≌△ADN (AAS) .
∴AM = DN. 同理可证 AN = DP.
∴AM + AN = DN + DP,即 MN = PN.
∴矩形 PQMN 是正方形.
总结:先证出四边形PQMN 是矩形,再证明一组邻边相等 (MN = NP).
1. 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
2. 正方形既是特殊的矩形,又是特殊的菱形. 具有矩形,菱形的所有性质.
正方形的性质
边
对边平行
四边相等
角
对角线
对角线相等
对角线互相垂直平分
每条对角线平分一组对角
:四个角相等且都是直角
课堂小结
3. 正方形的判定.
一个角是直角
或对角线相等
一组邻边相等
或对角线相互垂直
一组邻边相等
或对角线相互垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
对角线相等且互相垂直
18.2.3 正方形
八年级下
人教版
1. 理解正方形的概念,以及它与平行四边形、矩形、菱形之间的关系;
2. 能熟练运用正方形的性质和判定进行计算和证明.
学习目标
重点
难点
新课引入
正方形是我们熟悉的几何图形,它的边、角有什么特点?
正方形的四条边都相等,四个角都是直角.
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
两层含义
(1) 有一组邻边相等的平行四边形 (菱形)
(2) 并且有一个角是直角的平行四边形 (矩形)
新知学习
一 正方形的定义及其性质
由正方形的定义可知:
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.
思考
正方形既是特殊的矩形,又是特殊的菱形.正方形有哪些性质?
正方形具有矩形,菱形的所有性质.
平行四边形
矩形
菱形
正方形
归纳
正方形的性质
边
对边平行
四边相等
角
对角线
对角线相等
对角线互相垂直平分
每条对角线平分一组对角
:四个角相等且都是直角
A
B
D
C
O
探究
正方形是轴对称图形吗?如果是,它的对称轴是什么?
正方形是轴对称图形,有四条对称轴,分别是两条对角线所在的直线以及对边中点的连线.
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形 ABCD 是正方形,对角线 AC、BD 相交于点 O.
求证:△ABO、 △BCO、 △CDO、 △DAO 是全等的等腰直角三角形.
证明:∵四边形 ABCD 是正方形,
∴AC = BD,AC⊥BD,AO = CO = BO = DO
∴△ABO、△BCO、△CDO、△DAO 都是等腰直角三角形,
并且△ABO ≌△BCO ≌△CDO ≌△DAO.
图中共有多少个等腰直角三角形?
图中共有多少个等腰直角三角形?
8个,△ABO、△BCO、△CDO、△DAO、△ABD、△BCD、△ABC、△ACD.
探究1
怎样判定一个矩形是正方形?
二 正方形的判定
矩形:对角线相等且互相平分
正方形:对角线相等且互相垂直平分
对角线互相垂直?
已知:在矩形ABCD中,AC⊥BD.
求证:四边形ABCD是正方形.
证明: ∵四边形ABCD是矩形,
A
B
D
C
O
∴OA=OB=OC=OD,∠BAD=90 .
∵AC⊥BD,
∴AC是线段BD的垂直平分线.
∴AB=BC=CD=DA,
∴四边形ABCD是正方形.
同理:BD是线段AC的垂直平分线,
数学语言:
在矩形ABCD中, ∵ AC⊥BD,
∴四边形ABCD是正方形.
A
B
D
C
O
归纳
对角线互相垂直的矩形是正方形.
通过以上证明,我们得到正方形的一个判定:
探究2
怎样判定一个矩形是正方形?
矩形:对边相等
且平行
正方形:四边相等且对边平行
邻边相等?
已知:在矩形ABCD中,AB=BC.
求证:四边形ABCD是正方形.
证明: ∵四边形ABCD是矩形,
A
B
D
C
∴∠B=90 ,四边形ABCD是平行四边形.
∵AB=BC,
∴四边形ABCD是正方形.
归纳
有一组邻边相等的矩形是正方形.
通过以上证明,我们得到正方形的一个判定:
数学语言:
在矩形ABCD中, ∵AB=BC,
∴四边形ABCD是正方形.
A
B
D
C
O
探究3
怎样判定一个菱形是正方形?
菱形:对角线垂直且互相平分
正方形:对角线相等且互相垂直平分
对角线相等?
已知:在菱形ABCD中,AC,BD是两条对角线,且 AC=BD.
求证:四边形ABCD是正方形.
证明: ∵四边形ABCD是菱形,
A
B
D
C
O
∴AB=BC=CD=DA,AC⊥BD.
∵AC=BD,
∴OA=OB=OC=OD,
∴△AOB ,△BOC是等腰直角三角形,
∴四边形ABCD是正方形.
∴∠ABC=90 ,
归纳
对角线相等的菱形是正方形.
通过以上证明,我们得到正方形的一个判定:
数学语言:
在菱形ABCD中, ∵ AC=BD,
∴四边形ABCD是正方形.
A
B
D
C
O
探究4
怎样判定一个菱形是正方形?
菱形:对角相等
正方形:四个角相等,都为90°
有一个角为直角?
已知:在菱形ABCD中,∠A=90 .
求证:四边形ABCD是正方形.
证明: ∵四边形ABCD是菱形,
A
B
D
C
∴AB=BC=CD=DA,
四边形ABCD是平行四边形,
∵∠A=90 ,
∴四边形ABCD是正方形.
归纳
有一个角是直角的菱形是正方形.
通过以上证明,我们得到正方形的一个判定:
数学语言:
在菱形ABCD中,∵ ∠A=90 ,
∴四边形ABCD是正方形.
A
B
D
C
O
一个角是直角
或对角线相等
一组邻边相等
或对角线相互垂直
一组邻边相等
或对角线相互垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
对角线相等且互相垂直
归纳
例2 下列各句判定正方形的说法是否正确?
(1) 有一个角是直角的菱形是正方形. ( )
(2) 有一组邻边相等的矩形是正方形. ( )
(3) 对角线相等的菱形是正方形. ( )
(4) 对角线互相垂直的矩形是正方形. ( )
(5) 对角线相等且互相垂直的四边形是正方形. ( )
√
√
√
√
×
对角线相等且互相垂直平分的四边形是正方形.
或者对角线相等且互相垂直的平行四边形是正方形.
随堂练习
B
A.对角线互相垂直平分
B.对角线相等
C.对角线平分一组对角
D.四边相等
1.正方形具有而菱形不具有的性质是( ).
D
A.对角互补
B.对角线相等
C.四个角相等
D.对角线互相垂直
2.正方形具有而矩形不具有的性质是( ).
3.在正方形 ABCD 中,AB = 12 cm,对角线 AC、BD 相交于 O,则△ABO 的周长是 (____________) cm.
分析:△ABO 是等腰直角三角形,AB = 12 cm,
利用勾股定理,可以求出 OA = OB = cm,
所以△ABO 的周长是 ( ) cm.
3.如图,四边形ABCD是一块正方形场地.小华和小芳在AB边上取定了一点 E,测量知,EC=30m,EB=10m. 这块场地的面积和对角线分别是多少?
∴在Rt△EBC中
m.
解:∵四边形ABCD是正方形, ∴∠B=90 .
∴AB=BC=CD=DA=m,
∴场地的面积为,
对角线的长为
4.如图,正方形 ABCD,直线l1过点A,直线l2过点C,且l1∥l2,过点D作PN⊥l1垂足为N,交l2于点P,过点B作QM⊥l1垂足为M,交l2于点Q.
求证:四边形PNMQ是正方形.
证明:PN⊥l1,QM⊥l1,
∴PN∥QM,∠PNM =∠QMN = 90°.
∵l1∥l2,即 PQ∥NM,
∴四边形 PQMN 是矩形.
∵四边形 ABCD 是正方形,
∴∠BAD =90°,AB = AD ,
∴∠BAM +∠DAN = 90°.
又∠ADN +∠DAN = 90°,
∴∠BAM =∠ADN.
∴△BAM ≌△ADN (AAS) .
∴AM = DN. 同理可证 AN = DP.
∴AM + AN = DN + DP,即 MN = PN.
∴矩形 PQMN 是正方形.
总结:先证出四边形PQMN 是矩形,再证明一组邻边相等 (MN = NP).
1. 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
2. 正方形既是特殊的矩形,又是特殊的菱形. 具有矩形,菱形的所有性质.
正方形的性质
边
对边平行
四边相等
角
对角线
对角线相等
对角线互相垂直平分
每条对角线平分一组对角
:四个角相等且都是直角
课堂小结
3. 正方形的判定.
一个角是直角
或对角线相等
一组邻边相等
或对角线相互垂直
一组邻边相等
或对角线相互垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
对角线相等且互相垂直
