平均数(教学设计)人教版四年级下册数学
文档属性
| 名称 | 平均数(教学设计)人教版四年级下册数学 |

|
|
| 格式 | doc | ||
| 文件大小 | 782.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-12 00:00:00 | ||
图片预览



文档简介
《平均数》教学设计
一、教学内容解析
平均数是一个重要的刻画数据集中趋势的统计量,既可以用它来反映一组数据的一般情况,也可以用它进行不同组数据的比较。用平均数表示一组数据的情况,有直观、简明的特点,但也有自身的缺点,容易受极端数据的影响。
平均数是在第一学段已经理解了平均分及除法运算含义的基础上教学的。平均数的概念与学过的平均分的意义是不完全一样的。平均数具有虚拟性。
教材通过“移多补少”的方式使学生直观理解什么是平均数,再利用平均分的意义,使学生进一步明白:求几个数据的平均数,就相当于把这些数据的总和平均分成几份。由此,总结出求平均数的一般方法,实现从直观到抽象的过渡。
与实验教材相比,修订教材更加突出其统计意义。通过“两队人数不同,不能用总数比较”这一个思维的矛盾,促进学生进一步理解平均数的意义,进而发现运用平均数作比较的必要性。教学重点:理解平均数的意义,掌握求平均数的计算方法。
二、教学目标
1、会用“移多补少”和计算的方法求平均数,能用自己的语言解释平均数的实际意义,进而体会平均数的作用。
2、能在具体情境中根据平均数作出简单的判断,发展数据分析观念。
3、在解决问题的过程中培养提出问题、解决问题的能力,丰富对平均数的特点的认识。
三、教学重难点
理解平均数的统计意义。
四、教学过程
(一)体会平均数的作用,探索平均数的求法。
师:学校生活丰富多彩,每个班进行了踢毽子比赛,这是三个小组的比赛成绩。哪个小组的成绩好?
第一组(10 11 7 8)
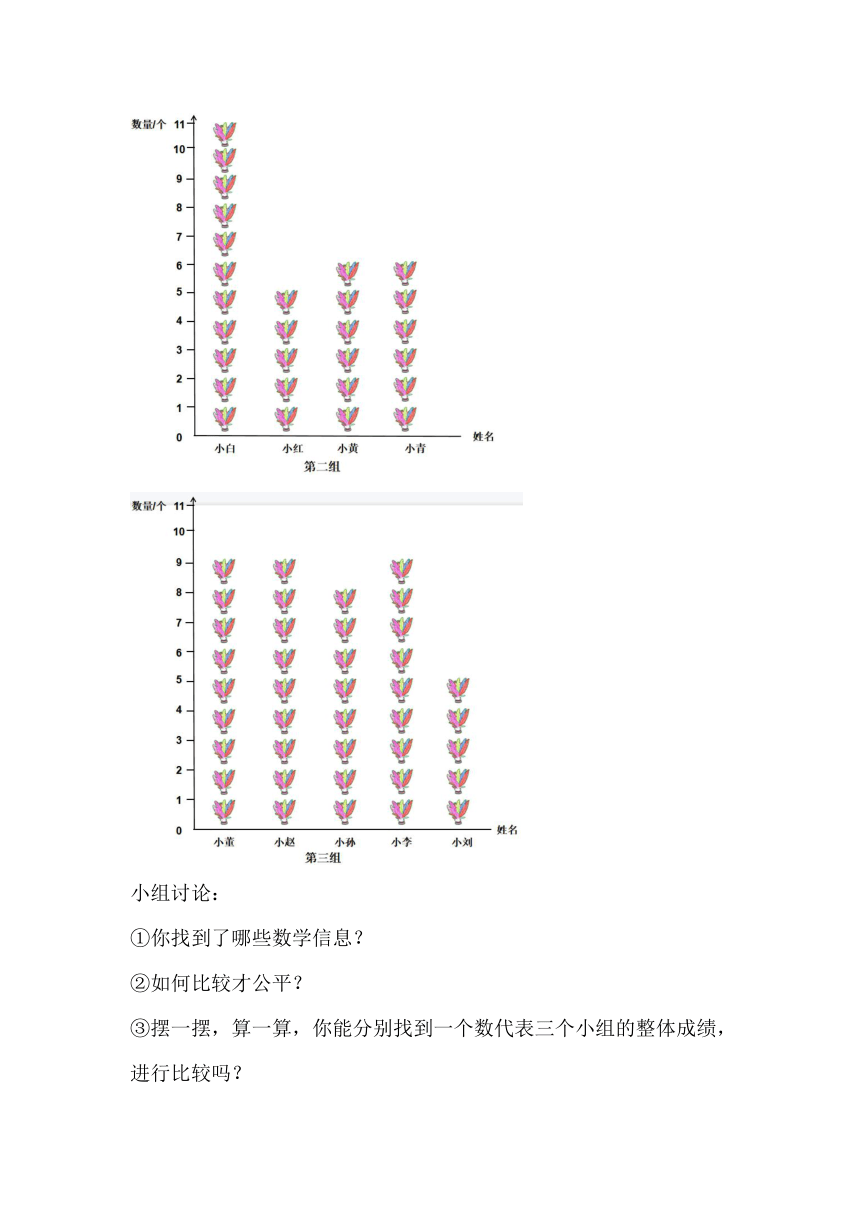
第二组(11 5 6 6)
第三组(9 9 8 9 5)
(象形统计图)
小组讨论:
①你找到了哪些数学信息?
②如何比较才公平?
③摆一摆,算一算,你能分别找到一个数代表三个小组的整体成绩,进行比较吗?
预设:
①矛盾冲突:
人数相等的情形,学生发现比较总数就可以
人数不等的情形,产生比较总数不公平的问题
②探索方法:
a.摆一摆,用“移多补少”的方法直观操作:
(象形统计图)
b.算一算,用“求和平分”的方法抽象计算:
第一组: (10+11+7+8)÷4
=36÷4
=9
第二组:(11+5+6+6)÷4
=28÷4
=7
第三组:(9+9+8+9+5)÷5
=40÷5
=8
师:请认真观察,在“移多补少”过程中,什么没变?与算式的每一步有什么联系?
预设:在“移多补少”过程中,总个数、人数没变,算式中括号里就是总个数,除数就是人数,也就是平均分成几份。
师:这两种方法有什么相同点?
预设:都是使原来几个不同的数变得同样多。
师:这样得到的数就是这组数据的平均数。(板书课题)
(二)丰富学生对平均数特点的认识
1、体会平均数的区间及虚拟性。
师:观察一下,平均数与这组每个数据比较,你发现了什么?
预设:①在最大数与最小数之间。(区间)
②第三组中,平均数与小红的个数相同,都是8,表示的意义一样吗?(平均数具有虚拟性,不是实际的数量,代表一组数据的整体情况)
2、发展数感,体会平均数的敏感性。
师:如果第一小组增加一个人,平均数会怎样?
预设:比平均数大,平均数会增大;比平均数小,平均数会减小;和平均数相等,平均数不变。(平均数随着数据的变化而变化)
师:增加的这个同学的成绩是4个,平均数大约在什么位置?可以怎么计算?
(10+11+7+8+4)÷5
=40÷5
=8
(三)
1、已知平均数和部分数据,求未知数据。
师:这是第四小组的成绩。你知道这个同学的成绩吗?
(条形统计图 8 12 5 ? 平均数9)
预设:
①通过“移多补少”的方法,发现12比9多3格,8比9少1格,5比9少4格,一共少5格,所以,应该比9多2格,是11。
②逆向思考,列式计算:
4×9-8-12-5=11,先求总数,依次减去前三位同学的成绩。
2、体会平均数容易受极端数据影响。
师:蛋糕店最近5天,平均每天销售12个草莓蛋糕,想一想这5天可能分别销售多少个草莓蛋糕?明天做多少草莓蛋糕合适呢?
预设:学生猜测的每个数据比较接近12,有多有少。12个比较合适。
师:如果是这种情况呢?画一画,有什么感受?明天该做多少个草莓蛋糕呢?
(条形统计图:7 6 8 9 ?)
预设:出现极端数据,第五天的数据特别大,平均数不能代表这一组数据的整体情况。准备12个不合适。
(四)回顾新知,梳理总结
师:通过这节课的学习,你有什么收获?
预设:①认识了平均数。
②求平均数的方法。
③平均数的特点。
一、教学内容解析
平均数是一个重要的刻画数据集中趋势的统计量,既可以用它来反映一组数据的一般情况,也可以用它进行不同组数据的比较。用平均数表示一组数据的情况,有直观、简明的特点,但也有自身的缺点,容易受极端数据的影响。
平均数是在第一学段已经理解了平均分及除法运算含义的基础上教学的。平均数的概念与学过的平均分的意义是不完全一样的。平均数具有虚拟性。
教材通过“移多补少”的方式使学生直观理解什么是平均数,再利用平均分的意义,使学生进一步明白:求几个数据的平均数,就相当于把这些数据的总和平均分成几份。由此,总结出求平均数的一般方法,实现从直观到抽象的过渡。
与实验教材相比,修订教材更加突出其统计意义。通过“两队人数不同,不能用总数比较”这一个思维的矛盾,促进学生进一步理解平均数的意义,进而发现运用平均数作比较的必要性。教学重点:理解平均数的意义,掌握求平均数的计算方法。
二、教学目标
1、会用“移多补少”和计算的方法求平均数,能用自己的语言解释平均数的实际意义,进而体会平均数的作用。
2、能在具体情境中根据平均数作出简单的判断,发展数据分析观念。
3、在解决问题的过程中培养提出问题、解决问题的能力,丰富对平均数的特点的认识。
三、教学重难点
理解平均数的统计意义。
四、教学过程
(一)体会平均数的作用,探索平均数的求法。
师:学校生活丰富多彩,每个班进行了踢毽子比赛,这是三个小组的比赛成绩。哪个小组的成绩好?
第一组(10 11 7 8)
第二组(11 5 6 6)
第三组(9 9 8 9 5)
(象形统计图)
小组讨论:
①你找到了哪些数学信息?
②如何比较才公平?
③摆一摆,算一算,你能分别找到一个数代表三个小组的整体成绩,进行比较吗?
预设:
①矛盾冲突:
人数相等的情形,学生发现比较总数就可以
人数不等的情形,产生比较总数不公平的问题
②探索方法:
a.摆一摆,用“移多补少”的方法直观操作:
(象形统计图)
b.算一算,用“求和平分”的方法抽象计算:
第一组: (10+11+7+8)÷4
=36÷4
=9
第二组:(11+5+6+6)÷4
=28÷4
=7
第三组:(9+9+8+9+5)÷5
=40÷5
=8
师:请认真观察,在“移多补少”过程中,什么没变?与算式的每一步有什么联系?
预设:在“移多补少”过程中,总个数、人数没变,算式中括号里就是总个数,除数就是人数,也就是平均分成几份。
师:这两种方法有什么相同点?
预设:都是使原来几个不同的数变得同样多。
师:这样得到的数就是这组数据的平均数。(板书课题)
(二)丰富学生对平均数特点的认识
1、体会平均数的区间及虚拟性。
师:观察一下,平均数与这组每个数据比较,你发现了什么?
预设:①在最大数与最小数之间。(区间)
②第三组中,平均数与小红的个数相同,都是8,表示的意义一样吗?(平均数具有虚拟性,不是实际的数量,代表一组数据的整体情况)
2、发展数感,体会平均数的敏感性。
师:如果第一小组增加一个人,平均数会怎样?
预设:比平均数大,平均数会增大;比平均数小,平均数会减小;和平均数相等,平均数不变。(平均数随着数据的变化而变化)
师:增加的这个同学的成绩是4个,平均数大约在什么位置?可以怎么计算?
(10+11+7+8+4)÷5
=40÷5
=8
(三)
1、已知平均数和部分数据,求未知数据。
师:这是第四小组的成绩。你知道这个同学的成绩吗?
(条形统计图 8 12 5 ? 平均数9)
预设:
①通过“移多补少”的方法,发现12比9多3格,8比9少1格,5比9少4格,一共少5格,所以,应该比9多2格,是11。
②逆向思考,列式计算:
4×9-8-12-5=11,先求总数,依次减去前三位同学的成绩。
2、体会平均数容易受极端数据影响。
师:蛋糕店最近5天,平均每天销售12个草莓蛋糕,想一想这5天可能分别销售多少个草莓蛋糕?明天做多少草莓蛋糕合适呢?
预设:学生猜测的每个数据比较接近12,有多有少。12个比较合适。
师:如果是这种情况呢?画一画,有什么感受?明天该做多少个草莓蛋糕呢?
(条形统计图:7 6 8 9 ?)
预设:出现极端数据,第五天的数据特别大,平均数不能代表这一组数据的整体情况。准备12个不合适。
(四)回顾新知,梳理总结
师:通过这节课的学习,你有什么收获?
预设:①认识了平均数。
②求平均数的方法。
③平均数的特点。
