17.4一元二次方程根与系数的关系 课件(共17张PPT)
文档属性
| 名称 | 17.4一元二次方程根与系数的关系 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1019.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 17:03:05 | ||
图片预览





文档简介
(共17张PPT)
17.4 一元二次程
与系数的关系
八年级下
沪科版
1. 理解一元二次方程根与系数的关系;
2. 了解一元二次方程根与系数的关系的简单应用.
学习目标
重点
难点
韦达是法国十六世纪最有影响的数学家之一.他是第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步.韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”).
韦达在欧洲被尊称为“代数学之父”.
韦达(1540-1603)
新课引入
探究
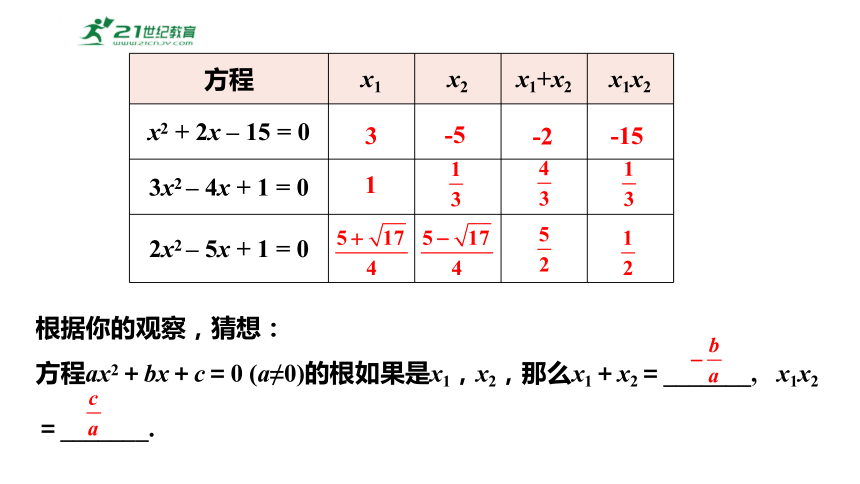
在前面17.2节中,我们学过,一元二次方程的每一个根都可由它的各项系数通过运算得到.
进一步,你是否注意到每个方程中的两根之间的关系?两根之和
(x1 + x2)、两根之积(x1x2)与该方程的各项系数之间有怎样的关系?填写下表,然后观察根与系数的关系:
新知学习
方程 x1 x2 x1+x2 x1x2
x2 + 2x – 15 = 0
3x2 – 4x + 1 = 0
2x2 – 5x + 1 = 0
3
-5
-2
-15
1
根据你的观察,猜想:
方程ax2+bx+c=0 (a≠0)的根如果是x1,x2,那么x1+x2=_______, x1x2
=_______.
你能证明上面的猜想吗?
我们知道,一元二次方程ax2+bx+c=0 (a≠0)的两根为:
归纳
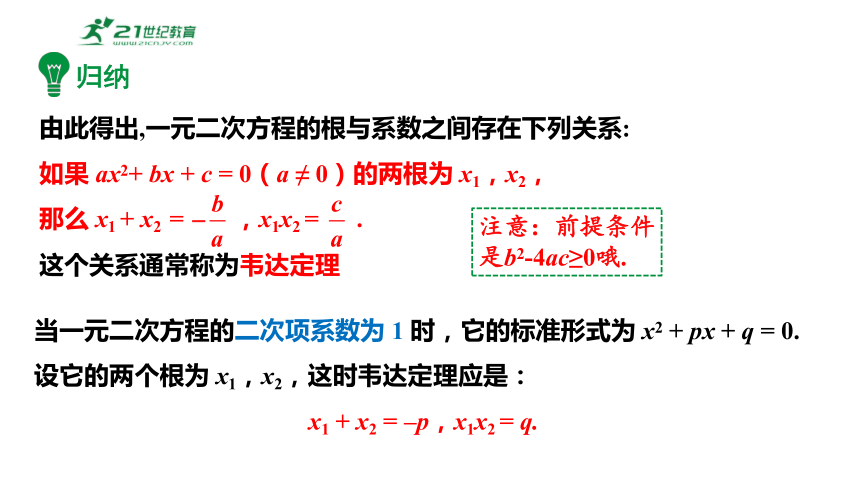
由此得出,一元二次方程的根与系数之间存在下列关系:
如果 ax2+ bx + c = 0(a ≠ 0)的两根为 x1,x2,
那么 x1 + x2 = ,x1x2 = .
这个关系通常称为韦达定理
当一元二次方程的二次项系数为 1 时,它的标准形式为 x2 + px + q = 0. 设它的两个根为 x1,x2,这时韦达定理应是:
x1 + x2 = –p,x1x2 = q.
注意:前提条件
是b2-4ac≥0哦.
例1 不解方程,求出方程的两根之和与两根之积:
(1) x2 + 3x - 5 = 0;
(2)2x2 - 3x - 5 = 0.
解: (1) 设两根为 x1、x2,由上述二次项系数为 1 的一元二次方程根与系数的关系,可得
x1 + x2 = -3,x1·x2 = -5.
解:(2) 方程两边同除以 2,得
设两根为 x1、x2,可得
例 2 已知关于 x 的方程 2x2 + kx – 4 = 0 的一个根是 –4,求它的另一个根及 k 的值.
解 设方程的另一个根是 x2,则
解方程组,得
答:方程的另一个根为 ,k 的值为 7.
已知一根,利用根与系数的关系求方程中待定字母的值的策略:
已知方程的一根求另一根,可以直接将一根代入方程中求出待定字母的值,然后再解方程求另一根.
也可以直接利用根与系数的关系求另一根及待定字母的值.
方法总结:
例 3 方程 2x2 – 3x + 1 = 0 的两个根记作x1,x2,不解方程,求出下列式
子的值:
(1)x1 – x2
解 (1)由韦达定理,得 x1 + x2 = , x1x2 = .
(x1 – x2)2 =(x1 + x2)2 – 4x1x2
∴ x1 – x2 =
(2)x12+ x22
解 (2)由韦达定理,得 x1 + x2 = , x1x2 = .
∴ x12+ x22=(x1 + x2)2 – 2x1x2
=( ) 2-2× =
(3)
解 (3)由韦达定理,得 x1 + x2 = , x1x2 = .
∴
=3
与两根和、两根积相关的常用变形公式
1.关于x的一元二次方程x2+2x-2m+1=0的两实数根之积为负,则实数m的取值范围是_________.
m>
2.已知一元二次方程 ax2 + bx + c = 0 ( a ≠ 0,b2 - 4ac≥0 ) 的两个根是 m,n ,那么下列关系式中正确的是 .
(1) am2 + bm + c = 0;(2) an2 + bn + c = 0;(3) m + n = - ;
(4) an2 + bm + c = 0;(5) am2 + bn+c=0;(6) mn = .
(1)(2)(3)(6)
随堂练习
x1x2=-(-2m+1)=2m-1<0
有两个相等的实根或有两个不相等的实根
8
3.如图是小明班级的长方形黑板,黑板的长与宽是一元二次方程x2-mx+3.36=0的两个根,已知黑板的宽为1.2 m,则这块黑板的周长为________m.
4. 已知关于 x 的一元二次方程 x2 - (2m - 2)x + m2 - 2m = 0 的两实数根为x1,x2,且 x12+x22 = 10,求 m 的值.
解:由题意可知 Δ = ( 2m - 2 )2 - 4(m - 2m) = 4 > 0,
∴无论 m 取任何值,方程有两个不相等的实数根.
∵x1 + x2 = 2m - 2, x1x2 = m - 2m,
∴x12 + x22 = (x1 + x2)2 - 2x1x2 = 10,
∴(2m - 2)2 - 2(m2 - 2m) = 10,
∴m2 - 2m - 3 = 0,
∴m = -1或 m = 3.
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
一元二次方程
的根与系数
的关系
内容
应用
课堂小结
17.4 一元二次程
与系数的关系
八年级下
沪科版
1. 理解一元二次方程根与系数的关系;
2. 了解一元二次方程根与系数的关系的简单应用.
学习目标
重点
难点
韦达是法国十六世纪最有影响的数学家之一.他是第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步.韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”).
韦达在欧洲被尊称为“代数学之父”.
韦达(1540-1603)
新课引入
探究
在前面17.2节中,我们学过,一元二次方程的每一个根都可由它的各项系数通过运算得到.
进一步,你是否注意到每个方程中的两根之间的关系?两根之和
(x1 + x2)、两根之积(x1x2)与该方程的各项系数之间有怎样的关系?填写下表,然后观察根与系数的关系:
新知学习
方程 x1 x2 x1+x2 x1x2
x2 + 2x – 15 = 0
3x2 – 4x + 1 = 0
2x2 – 5x + 1 = 0
3
-5
-2
-15
1
根据你的观察,猜想:
方程ax2+bx+c=0 (a≠0)的根如果是x1,x2,那么x1+x2=_______, x1x2
=_______.
你能证明上面的猜想吗?
我们知道,一元二次方程ax2+bx+c=0 (a≠0)的两根为:
归纳
由此得出,一元二次方程的根与系数之间存在下列关系:
如果 ax2+ bx + c = 0(a ≠ 0)的两根为 x1,x2,
那么 x1 + x2 = ,x1x2 = .
这个关系通常称为韦达定理
当一元二次方程的二次项系数为 1 时,它的标准形式为 x2 + px + q = 0. 设它的两个根为 x1,x2,这时韦达定理应是:
x1 + x2 = –p,x1x2 = q.
注意:前提条件
是b2-4ac≥0哦.
例1 不解方程,求出方程的两根之和与两根之积:
(1) x2 + 3x - 5 = 0;
(2)2x2 - 3x - 5 = 0.
解: (1) 设两根为 x1、x2,由上述二次项系数为 1 的一元二次方程根与系数的关系,可得
x1 + x2 = -3,x1·x2 = -5.
解:(2) 方程两边同除以 2,得
设两根为 x1、x2,可得
例 2 已知关于 x 的方程 2x2 + kx – 4 = 0 的一个根是 –4,求它的另一个根及 k 的值.
解 设方程的另一个根是 x2,则
解方程组,得
答:方程的另一个根为 ,k 的值为 7.
已知一根,利用根与系数的关系求方程中待定字母的值的策略:
已知方程的一根求另一根,可以直接将一根代入方程中求出待定字母的值,然后再解方程求另一根.
也可以直接利用根与系数的关系求另一根及待定字母的值.
方法总结:
例 3 方程 2x2 – 3x + 1 = 0 的两个根记作x1,x2,不解方程,求出下列式
子的值:
(1)x1 – x2
解 (1)由韦达定理,得 x1 + x2 = , x1x2 = .
(x1 – x2)2 =(x1 + x2)2 – 4x1x2
∴ x1 – x2 =
(2)x12+ x22
解 (2)由韦达定理,得 x1 + x2 = , x1x2 = .
∴ x12+ x22=(x1 + x2)2 – 2x1x2
=( ) 2-2× =
(3)
解 (3)由韦达定理,得 x1 + x2 = , x1x2 = .
∴
=3
与两根和、两根积相关的常用变形公式
1.关于x的一元二次方程x2+2x-2m+1=0的两实数根之积为负,则实数m的取值范围是_________.
m>
2.已知一元二次方程 ax2 + bx + c = 0 ( a ≠ 0,b2 - 4ac≥0 ) 的两个根是 m,n ,那么下列关系式中正确的是 .
(1) am2 + bm + c = 0;(2) an2 + bn + c = 0;(3) m + n = - ;
(4) an2 + bm + c = 0;(5) am2 + bn+c=0;(6) mn = .
(1)(2)(3)(6)
随堂练习
x1x2=-(-2m+1)=2m-1<0
有两个相等的实根或有两个不相等的实根
8
3.如图是小明班级的长方形黑板,黑板的长与宽是一元二次方程x2-mx+3.36=0的两个根,已知黑板的宽为1.2 m,则这块黑板的周长为________m.
4. 已知关于 x 的一元二次方程 x2 - (2m - 2)x + m2 - 2m = 0 的两实数根为x1,x2,且 x12+x22 = 10,求 m 的值.
解:由题意可知 Δ = ( 2m - 2 )2 - 4(m - 2m) = 4 > 0,
∴无论 m 取任何值,方程有两个不相等的实数根.
∵x1 + x2 = 2m - 2, x1x2 = m - 2m,
∴x12 + x22 = (x1 + x2)2 - 2x1x2 = 10,
∴(2m - 2)2 - 2(m2 - 2m) = 10,
∴m2 - 2m - 3 = 0,
∴m = -1或 m = 3.
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
一元二次方程
的根与系数
的关系
内容
应用
课堂小结
