18.2勾股定理的逆定理 课件(共26张PPT)
文档属性
| 名称 | 18.2勾股定理的逆定理 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
18.2 勾股定理的逆定理
八年级下
沪科版
1.理解勾股定理逆定理的具体内容.
2.能利用勾股定理的逆定理判断一个三角形是直角三角形.
3.掌握勾股数的应用.
学习目标
重点
难点
难点
在古代,人类还没有发明出直角尺、圆规、量角器等作图工具,人们是怎么画直角三角形的呢?
古埃及人在建造金字塔的时候,就面对这样一个问题:该如何得到一个直角?
不借助任何工具,你能画出一个直角吗?
新课引入
据说,几千年前的古埃及人就已经知道,在一根绳子上连续打上等距离的13个结,然后,用钉子将第1个与第13个结钉在一起,拉紧绳子, 再在第4个和第8个结处各钉上一个钉子,如图. 这样围成的三角形中,最长边所对的角就是直角.
新知学习
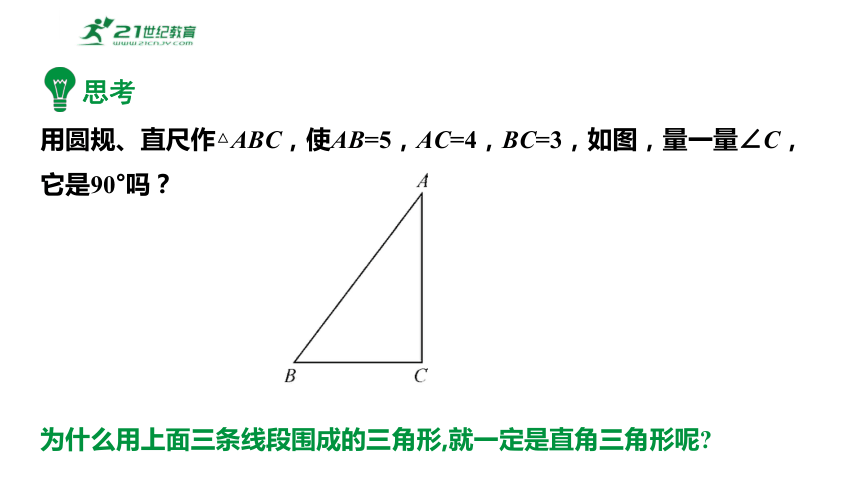
用圆规、直尺作△ABC,使AB=5,AC=4,BC=3,如图,量一量∠C,它是90°吗?
为什么用上面三条线段围成的三角形,就一定是直角三角形呢
思考
这个问题意味着,如果围成的三角形的三边长分别为3,4,5,它们满足关系“32+42=52”,那么围成的三角形是直角三角形.
画画看,如果三角形的三边长分别为2.5 cm,6 cm,6.5 cm,它们满足关系“2.52+62=6.52”,画出的三角形是直角三角形吗
换成三边分别为4 cm,7.5 cm,8. 5 cm,再试一试.
画出的三角形是直角三角形.
画出的三角形也是直角三角形.
由上面几个例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
你能证明吗?
△ABC≌ △ A′B′C′
?
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
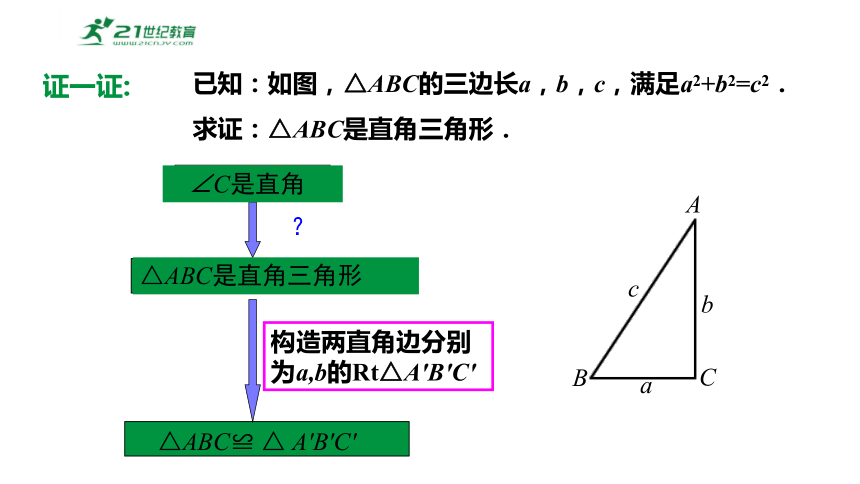
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
证一证:
证明:如图,作Rt△A′B′C′,使∠C′=90°,A′C′=b,B′C′=a,
∴△ABC≌ △A′B′C′(SSS),
∴∠C= ∠C′=90° , 即△ABC是直角三角形.
则
A
C
a
B
b
c
归纳
勾股定理的逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
符号语言:
∵a2 + b2 = c2 ,
∴∠C = 90°.
A
B
C
a
b
c
例1 根据下列三角形的三边a,b,c的值,判断△ABC是不是直角三角形. 如果是,指出哪条边所对的角是直角.
(1)a=7,b=24,c=25;
解:(1)∵最大边是c=25,c2=625,
a2+b2=72 +242 =625 ,
∴ a2+b2=c2
∴△ABC是直角三角形,最大边c所对的角是直角.
(2)a=7,b=8,c =11.
(2) ∵最大边是c=11,c2=121,
a2+b2=72 +82 =113 ,
∴ a2+b2 ≠ c2
∴△ABC不是直角三角形 .
方法总结:1. 勾股定理的逆定理是判定直角三角形的一个依据,在判定时不能说“在直角三角形中”“直角边”“斜边”,因为还没有确定是直角三角形 .
2.a2+b2=c2 只是一种表现形式,满足a2=b2+c2或b2=a2+c2的也是直角三角形,只是这时a或 b 为斜边 .
利用边的关系判定直角三角形的步骤
(1) “找”: 找出三角形三边中的最长边 .
(2) “算”: 计算其他两边的平方和与最长边的平方 .
(3) “判”: 若两者相等,则这个三角形是直角三角形,否则不是 .
归纳
例2 已知:在△ABC中,三条边长分别为a=n2 – 1,b=2n,c=n2+1(n>1,n为正整数).求证:△ABC为直角三角形.
证明 ∵a2+b2=(n2 – 1)2+(2n)2
= n4 – 2n2+1+4n2
= n4+2n2+1
= (n2+1)2=c2
∴△ABC为直角三角形.(勾股定理的逆定理)
像这样能构成直角三角形的三条边的三个整数,你知道叫做什么吗
1.勾股数 能够成为直角三角形三条边长度的三个正整数,叫做勾股数 .
2.勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方 .
归纳
3. 判别一组数是否为勾股数的一般步骤
(1)“看”: 看是不是三个正整数 .
(2)“找”: 找最大数 .
(3)“算”: 计算最大数的平方与两个较小数的平方和 .
(4)“判”: 若两者相等,则这三个数是一组勾股数,否则,不是一组勾股数 .
例3 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,
CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:连接BD.在Rt△ABD中,
由勾股定理得 BD2=AB2+AD2,
∴BD=5m.
又∵CD=12cm,BC=13cm,
∴BC2=CD2+BD2,△BDC是直角三角形.
∴S四边形ABCD=SRt△BCD - SRt△ABD
= BD·CD - AB·AD=24 (cm2).
C
B
A
D
归纳
求不规则图形的面积解题思路:
用割补法,将不规则图形转化成规则图形,再求解。
C
B
A
D
补:
A
D
B
C
割:
勾股定理与其逆定理的关系
定理 勾股定理 勾股定理的逆定理
区别 (1)勾股定理是以“一个三角形是直角三角形”为条件,进而得到这个直角三角形三边长的关系,即 a2+b2=c2( c 为斜边长);
(2)勾股定理是根据直角三角形探求边的关系,体现了由形到数的转化 (1)勾股定理的逆定理是以“一个三角形的三边长 a, b, c 满足 a2+b2=c2”为条件,进而得到这个三角形为直角三角形;
(2)勾股定理的逆定理是由三角形的三边关系探求三角形的形状,体现了由数到形的转化
联系 勾股定理和勾股定理的逆定理的条件和结论相反,勾股定理是直角三角形的性质,而其逆定理是直角三角形的判定,勾股定理及其逆定理都与直角三角形有关 1.下列四组数中,不是勾股数的一组是( )
A.5,12,13 B.3,4,5 C.6,8,10 D.6,7,8
D
2. 一个三角形的三边的长分别是 15cm,20cm,25cm,则这个三角形的面积是 ( ) cm2.
A. 250 B. 150 C. 200 D. 不能确定
B
随堂练习
∵15 +20 =25
∴这个三角形为直角三角形,斜边长为25cm,直角边分别为15cm,20cm
∴三角形面积=15×20÷2=150cm2
3. 如图,在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为________.
16π
A
B
C
17
15
AB=8
4.如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
A
D
B
C
3
4
13
12
解:连接AC.
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
A
D
B
C
3
4
13
12
5. 一艘在海上朝正北方向航行的轮船,在航行 240 海里时方位仪坏了,凭经验,船长指挥船左转 90°,继续航行 70 海里,则距出发地 250 海里,你能判断船转弯后,是否沿正西方向行驶?
A
B
C
北
解:船转弯后,是沿正西方向航行的. 理由如下:
由题意画出相应的图形,依题意可知:
AB = 240 海里,BC = 70 海里,AC = 250 海里.
在△ABC 中
AC2 - AB2 = 2502 - 2402
= 4900 = 702 = BC2
即,AB2 + BC2 = AC2,所以△ABC 是直角三角形,且∠ABC = 90°.
所以,是沿正西方向航行的.
答:船转弯后,是沿正西方向航行的.
A
B
C
北
勾股定理的逆定理
勾股定理的逆定理:
如果三角形的三边长 a,b,c 满足a2+b2=c2,
那么这个三角形是直角三角形.
勾股数:满足 a2+b2=c2 的三个正整数
课堂小结
18.2 勾股定理的逆定理
八年级下
沪科版
1.理解勾股定理逆定理的具体内容.
2.能利用勾股定理的逆定理判断一个三角形是直角三角形.
3.掌握勾股数的应用.
学习目标
重点
难点
难点
在古代,人类还没有发明出直角尺、圆规、量角器等作图工具,人们是怎么画直角三角形的呢?
古埃及人在建造金字塔的时候,就面对这样一个问题:该如何得到一个直角?
不借助任何工具,你能画出一个直角吗?
新课引入
据说,几千年前的古埃及人就已经知道,在一根绳子上连续打上等距离的13个结,然后,用钉子将第1个与第13个结钉在一起,拉紧绳子, 再在第4个和第8个结处各钉上一个钉子,如图. 这样围成的三角形中,最长边所对的角就是直角.
新知学习
用圆规、直尺作△ABC,使AB=5,AC=4,BC=3,如图,量一量∠C,它是90°吗?
为什么用上面三条线段围成的三角形,就一定是直角三角形呢
思考
这个问题意味着,如果围成的三角形的三边长分别为3,4,5,它们满足关系“32+42=52”,那么围成的三角形是直角三角形.
画画看,如果三角形的三边长分别为2.5 cm,6 cm,6.5 cm,它们满足关系“2.52+62=6.52”,画出的三角形是直角三角形吗
换成三边分别为4 cm,7.5 cm,8. 5 cm,再试一试.
画出的三角形是直角三角形.
画出的三角形也是直角三角形.
由上面几个例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
你能证明吗?
△ABC≌ △ A′B′C′
?
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
证一证:
证明:如图,作Rt△A′B′C′,使∠C′=90°,A′C′=b,B′C′=a,
∴△ABC≌ △A′B′C′(SSS),
∴∠C= ∠C′=90° , 即△ABC是直角三角形.
则
A
C
a
B
b
c
归纳
勾股定理的逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
符号语言:
∵a2 + b2 = c2 ,
∴∠C = 90°.
A
B
C
a
b
c
例1 根据下列三角形的三边a,b,c的值,判断△ABC是不是直角三角形. 如果是,指出哪条边所对的角是直角.
(1)a=7,b=24,c=25;
解:(1)∵最大边是c=25,c2=625,
a2+b2=72 +242 =625 ,
∴ a2+b2=c2
∴△ABC是直角三角形,最大边c所对的角是直角.
(2)a=7,b=8,c =11.
(2) ∵最大边是c=11,c2=121,
a2+b2=72 +82 =113 ,
∴ a2+b2 ≠ c2
∴△ABC不是直角三角形 .
方法总结:1. 勾股定理的逆定理是判定直角三角形的一个依据,在判定时不能说“在直角三角形中”“直角边”“斜边”,因为还没有确定是直角三角形 .
2.a2+b2=c2 只是一种表现形式,满足a2=b2+c2或b2=a2+c2的也是直角三角形,只是这时a或 b 为斜边 .
利用边的关系判定直角三角形的步骤
(1) “找”: 找出三角形三边中的最长边 .
(2) “算”: 计算其他两边的平方和与最长边的平方 .
(3) “判”: 若两者相等,则这个三角形是直角三角形,否则不是 .
归纳
例2 已知:在△ABC中,三条边长分别为a=n2 – 1,b=2n,c=n2+1(n>1,n为正整数).求证:△ABC为直角三角形.
证明 ∵a2+b2=(n2 – 1)2+(2n)2
= n4 – 2n2+1+4n2
= n4+2n2+1
= (n2+1)2=c2
∴△ABC为直角三角形.(勾股定理的逆定理)
像这样能构成直角三角形的三条边的三个整数,你知道叫做什么吗
1.勾股数 能够成为直角三角形三条边长度的三个正整数,叫做勾股数 .
2.勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方 .
归纳
3. 判别一组数是否为勾股数的一般步骤
(1)“看”: 看是不是三个正整数 .
(2)“找”: 找最大数 .
(3)“算”: 计算最大数的平方与两个较小数的平方和 .
(4)“判”: 若两者相等,则这三个数是一组勾股数,否则,不是一组勾股数 .
例3 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,
CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:连接BD.在Rt△ABD中,
由勾股定理得 BD2=AB2+AD2,
∴BD=5m.
又∵CD=12cm,BC=13cm,
∴BC2=CD2+BD2,△BDC是直角三角形.
∴S四边形ABCD=SRt△BCD - SRt△ABD
= BD·CD - AB·AD=24 (cm2).
C
B
A
D
归纳
求不规则图形的面积解题思路:
用割补法,将不规则图形转化成规则图形,再求解。
C
B
A
D
补:
A
D
B
C
割:
勾股定理与其逆定理的关系
定理 勾股定理 勾股定理的逆定理
区别 (1)勾股定理是以“一个三角形是直角三角形”为条件,进而得到这个直角三角形三边长的关系,即 a2+b2=c2( c 为斜边长);
(2)勾股定理是根据直角三角形探求边的关系,体现了由形到数的转化 (1)勾股定理的逆定理是以“一个三角形的三边长 a, b, c 满足 a2+b2=c2”为条件,进而得到这个三角形为直角三角形;
(2)勾股定理的逆定理是由三角形的三边关系探求三角形的形状,体现了由数到形的转化
联系 勾股定理和勾股定理的逆定理的条件和结论相反,勾股定理是直角三角形的性质,而其逆定理是直角三角形的判定,勾股定理及其逆定理都与直角三角形有关 1.下列四组数中,不是勾股数的一组是( )
A.5,12,13 B.3,4,5 C.6,8,10 D.6,7,8
D
2. 一个三角形的三边的长分别是 15cm,20cm,25cm,则这个三角形的面积是 ( ) cm2.
A. 250 B. 150 C. 200 D. 不能确定
B
随堂练习
∵15 +20 =25
∴这个三角形为直角三角形,斜边长为25cm,直角边分别为15cm,20cm
∴三角形面积=15×20÷2=150cm2
3. 如图,在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为________.
16π
A
B
C
17
15
AB=8
4.如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
A
D
B
C
3
4
13
12
解:连接AC.
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
A
D
B
C
3
4
13
12
5. 一艘在海上朝正北方向航行的轮船,在航行 240 海里时方位仪坏了,凭经验,船长指挥船左转 90°,继续航行 70 海里,则距出发地 250 海里,你能判断船转弯后,是否沿正西方向行驶?
A
B
C
北
解:船转弯后,是沿正西方向航行的. 理由如下:
由题意画出相应的图形,依题意可知:
AB = 240 海里,BC = 70 海里,AC = 250 海里.
在△ABC 中
AC2 - AB2 = 2502 - 2402
= 4900 = 702 = BC2
即,AB2 + BC2 = AC2,所以△ABC 是直角三角形,且∠ABC = 90°.
所以,是沿正西方向航行的.
答:船转弯后,是沿正西方向航行的.
A
B
C
北
勾股定理的逆定理
勾股定理的逆定理:
如果三角形的三边长 a,b,c 满足a2+b2=c2,
那么这个三角形是直角三角形.
勾股数:满足 a2+b2=c2 的三个正整数
课堂小结
