19.1多边形内角和 课件(共37张PPT)
文档属性
| 名称 | 19.1多边形内角和 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 17:03:05 | ||
图片预览








文档简介
(共37张PPT)
19.1 多边形内角和
八年级下
沪科版
1.了解多边形、正多边形及多边形的边、顶点、内角、对角线的概念;
会用表示顶点的字母表示多边形.
2.探索、总结并掌握多边形的内角和、外角和定理.
3.了解四边形具有不稳定性.
学习目标
重点
重点
新知学习
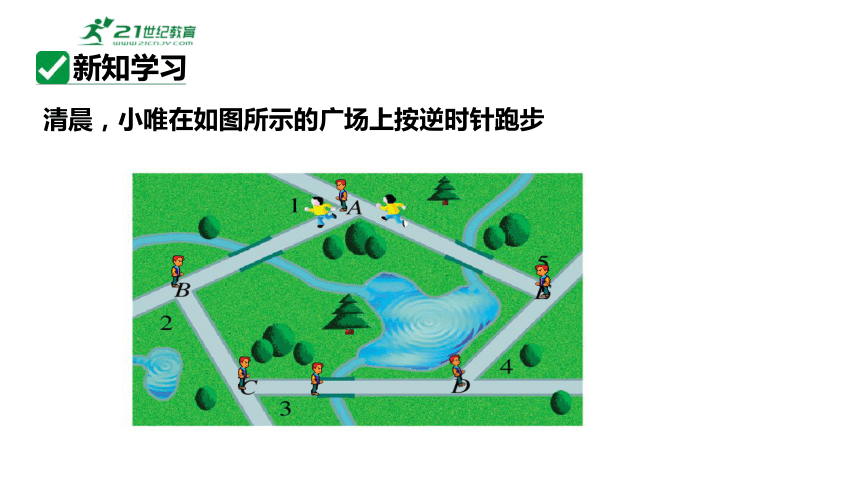
清晨,小唯在如图所示的广场上按逆时针跑步
问题2 观察小明跑步的过程,类比三角形的概念,你能说出什么是多边形吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
问题1 什么是三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
思考
问题3比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?怎样命名多边形呢?
这是因为三角形中的三个顶点肯定都在同一个平面内,而四点,五点,甚至更多的点就有可能不在同一个平面内.
问题4 根据图示,类比三角形的有关概念,说明什么是多边形的顶点、边、内角、外角.
相关概念:
1.组成多边形的线段叫做多边形的边.
2.相邻两边的公共端点叫做多边形的顶点.
3.多边形中相邻两边组成的角叫做多边形的内角,简称多边形的角;
4.在顶点处一边与另一边的延长线所组成的角叫做多边形的外角.
5.多边形中连接不相邻的两个顶点的线段,叫做多边形的对角线 .
6
线段 AC 是五边形 ABCDE 的一条对角线,多边形的对角线通常用虚线表示.
三角形
六边形
四边形
八边形
…
五边形
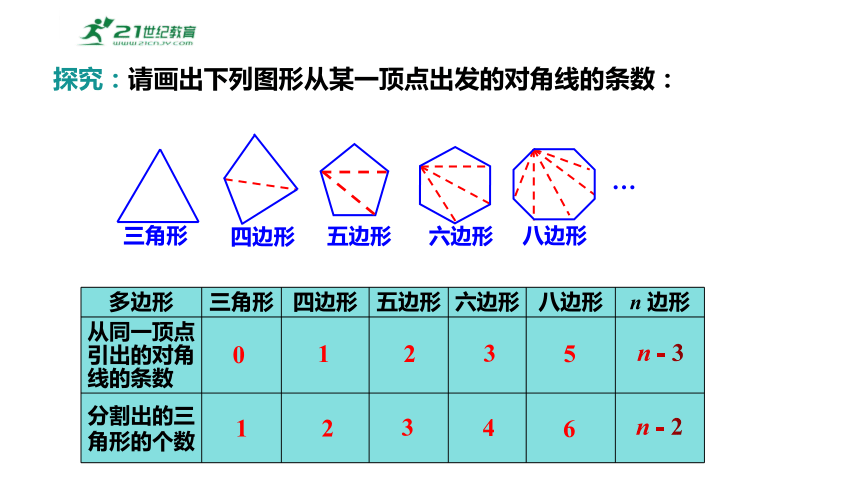
探究:请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n 边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n - 3
1
2
3
4
6
n - 2
从 n (n≥3) 边形的一个顶点可以作出 (n - 3) 条对角线.
将多边形分成 (n - 2) 个三角形.
n (n≥3) 边形共有对角线 条.
总结:
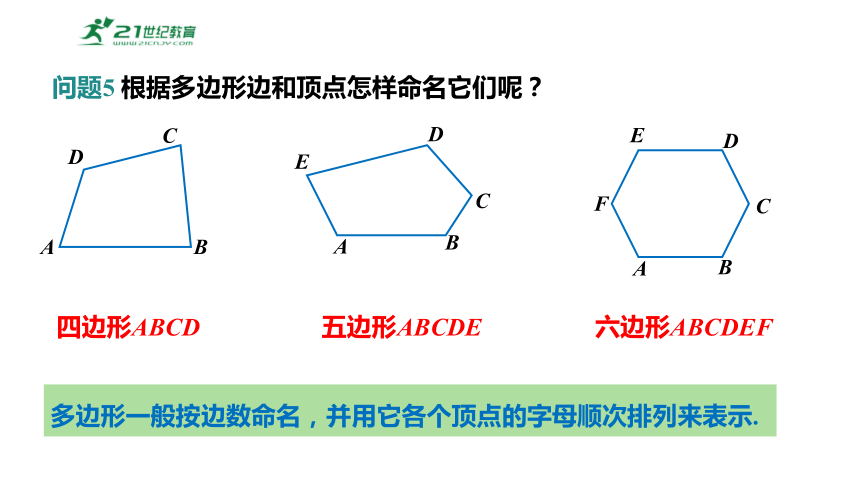
多边形一般按边数命名,并用它各个顶点的字母顺次排列来表示.
四边形ABCD
五边形ABCDE
六边形ABCDEF
问题5 根据多边形边和顶点怎样命名它们呢?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
问题6 请同学们用量角器和直尺度量一下问题二中的三幅图片中的边和内角有什么不同?
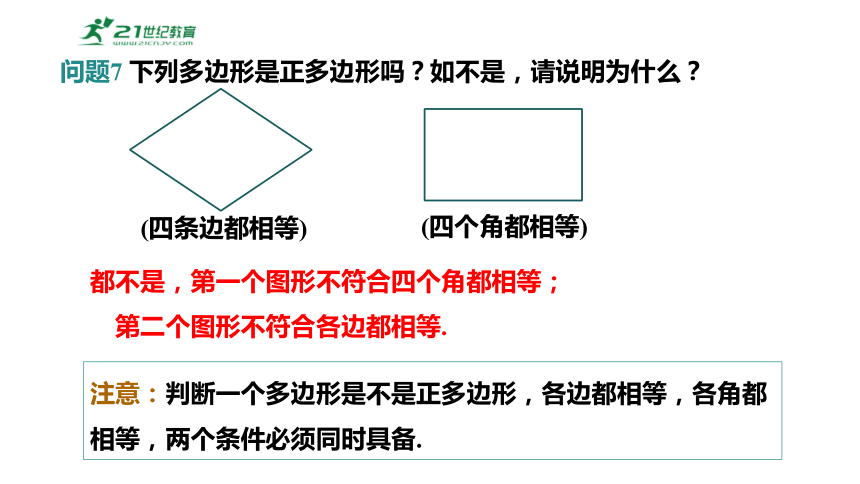
多边形中,如果各条边都相等,各个内角都相等,这样的多边形叫做正多边形 .
图(1)(2)中的边和内角不全相等,图(3)的边和内角都相等
问题7 下列多边形是正多边形吗?如不是,请说明为什么?
(四条边都相等)
(四个角都相等)
都不是,第一个图形不符合四个角都相等;
第二个图形不符合各边都相等.
注意:判断一个多边形是不是正多边形,各边都相等,各角都相等,两个条件必须同时具备.
问题8 请分别画出下列两个图形各边所在的直线,你能得到什么结论?
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形就是凸多边形,如图(1).
而图(2)所示的图形就不是凸多边形.
(1)
(2)
本教科书中所研究的都是凸多边形.
A
B
C
D
A
B
C
D
探究
问题2 你知道长方形和正方形的内角和是多少度吗?
问题1 三角形的内角和是多少度?
三角形内角和是 180°.
都是 360°.
问题3 猜想任意四边形的内角和是多少度?
猜想:四边形 ABCD 的内角和是 360°.
问题4 你能用以前学过的知识证明一下你的结论吗?
A
B
C
D
如图,连接AC,能推得四边形的内角和吗
这里的AC是四边形ABCD的一条对角线.
四边形的内角和等于两个三角形内角和之和:
180°×2 = 360°
方法1:
该四边形被分成三个三角形,
所以四边形 ABCD 的内角和为
180°×3 - (∠AEB+∠AED+∠CED)
= 180°×3 - 180°
= 360°.
方法2:
如图,在 BC 边上任取一点 E,连接 AE,DE,能推得四边形内角和吗
A
B
C
D
E
方法3:
如图,在四边形内任取一点О,连接OA,OB,OC, OD,也能推得四边形内角和吗
四边形的内角和等于 4 个三角形内角和之和,减去一个圆周角:
180°×4 - 360° = 360°
A
B
C
D
E
A
B
C
D
P
如图,在四边形外任取一点 P,连接 PA、PB、PC、PD 将四边形变成有一个公共顶点的四个三角形.
所以四边形 ABCD 的内角和为
180°×3 - 180° = 360°.
结论: 四边形的内角和为360°.
方法4:
以上这四种方法都运用了转化的思想,把四边形分割成三角形,转化为已学的三角形内角和进行求解.
多边形的问题也可以通过添加辅助线转化为三角形问题来解决.
问题5 你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗
A
C
D
E
B
A
B
C
D
E
F
内角和为 180°×3 = 540°.
内角和为 180°×4 = 720°.
边数 图形 从多边形的一顶点引出的对角线条数 分割出的三角形个数 多边形内角和
三角形
四边形
五边形
六边形
···
n 边形
···
0
n - 3
1
2
3
1
2
3
4
n - 2
( n -2 )·180°
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
···
···
···
由特殊到一般
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
外部
转化思想
多边形的内角和公式
n 边形的内角和等于 (n - 2)×180°.
总结
小唯每跑完一圈,身体转过的角度之和是多少?
思考
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角. (如图所示:∠1,∠2,∠3,∠4,∠5)
在多边形的每个顶点处取一个外角,它们的和叫做多边形的外角和.
如图,在五边形的每个顶点处各取一个外角.
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:五个外角加上它们分别相邻的五个内角和是多少?
互补
5×180° = 900°
五边形的外角和
= 360°.
= 5个平角和
-五边形内角和
= 5×180°
-(5-2) × 180°
结论:五边形的外角和等于 360°.
问题3:这五个平角和与五边形的内角和、外角和有什么关系?
归纳
定理: n 边形的外角和等于 360°(n 为不小于 3 的整数).
注意:多边形的外角和与边数无关
问题4: 一个n边形的外角和是多少度?
五边形的外角和=180°×5-五边形内角和=360°
六边形的外角和=180°×6-六边形内角和=360°
问题5:你能推导出正n边形的内角与外角公式吗?
n 边形的内角和等于(n-2)·180°,所以
每个内角等于 ;
每个外角等于 .
正n边形的每个内角都相等,每个外角也都相等.
活动的铁栅栏门,正是由于四边形可以变动,所以它可以拉开,也可以收拢.
用来固定相机的三脚架,三角形不能变动,所以调整好高度就不会动了.
请你根据生活中的多边形讨论多边形的物体稳定吗?
讨论
三角形的三边一旦确定,其形状和大小就确定了,所以三角形具有稳定性;四边形各条边的长确定后,其形状不能确定,因此四边形具有不稳定性
归纳
1. 下列多边形中,不是凸多边形的是( )
A
B
C
D
B
随堂练习
2. 一个多边形从一个顶点可引对角线 3 条,这个多边形
的内角和等于( )
A. 360° B. 540° C. 720° D. 900°
C
4. 过八边形的一个顶点画对角线,把这个八边形分成 个三角形.
6
3.如图,将两个相同的正六边形螺母摆放在桌面上,则∠1的度数为____°.
60
6.已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
解:设这个多边形的内角为7x °,外角为2x°,
根据题意得:
7x+2x=180,
解得: x=20.
即每个内角是140 °,每个外角是40 °.
360÷40 °=9.
答:这个多边形是九边形.
7. 一个多边形的内角和为 1800°,截去一个角后,求得到的多边形的内角和.
解:∵ 1800÷180=10,
∴ 原多边形边数为10+2=12.
∵ 一个多边形截去一个内角后,边数可能减 1,可能不变,也可能加 1,
∴ 新多边形的边数可能是 11,12,13.
∴ 新多边形的内角和可能是 1620°,1800°,1980°.
能力提升:如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7 的度数.
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形的内角和
=540°.
8
9
多边形的概念
定义
在平面内,由若干条 同一条直线上的线段首尾顺次相接组成的封闭图形叫做多边形.
相关
概念
1. 叫做多边形的边.
2. 叫做多边形的顶点.
3. 叫做多边形的内角,简称多边形的角;
4. 叫做多边形的外角.
5. 叫做多边形的对角线 .
正多边形
如果 ,这样的多边形叫做正多边形 .
课堂小结
不在
组成多边形的线段
相邻两边的公共端点
多边形中相邻两边组成的角
在顶点处一边与另一边的延长线所组成的角
多边形中连接不相邻的两个顶点的线段,
各条边都相等,各个内角都相等
多边形的性质
内角和计算公式
(n - 2)×180°(n≥3,且为整数)
外角和
多边形的外角和等于 .
特别注意:与边数无关
正多边形
内角= ,外角=
四边形
具有
不稳定性
360°
19.1 多边形内角和
八年级下
沪科版
1.了解多边形、正多边形及多边形的边、顶点、内角、对角线的概念;
会用表示顶点的字母表示多边形.
2.探索、总结并掌握多边形的内角和、外角和定理.
3.了解四边形具有不稳定性.
学习目标
重点
重点
新知学习
清晨,小唯在如图所示的广场上按逆时针跑步
问题2 观察小明跑步的过程,类比三角形的概念,你能说出什么是多边形吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
问题1 什么是三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
思考
问题3比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?怎样命名多边形呢?
这是因为三角形中的三个顶点肯定都在同一个平面内,而四点,五点,甚至更多的点就有可能不在同一个平面内.
问题4 根据图示,类比三角形的有关概念,说明什么是多边形的顶点、边、内角、外角.
相关概念:
1.组成多边形的线段叫做多边形的边.
2.相邻两边的公共端点叫做多边形的顶点.
3.多边形中相邻两边组成的角叫做多边形的内角,简称多边形的角;
4.在顶点处一边与另一边的延长线所组成的角叫做多边形的外角.
5.多边形中连接不相邻的两个顶点的线段,叫做多边形的对角线 .
6
线段 AC 是五边形 ABCDE 的一条对角线,多边形的对角线通常用虚线表示.
三角形
六边形
四边形
八边形
…
五边形
探究:请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n 边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n - 3
1
2
3
4
6
n - 2
从 n (n≥3) 边形的一个顶点可以作出 (n - 3) 条对角线.
将多边形分成 (n - 2) 个三角形.
n (n≥3) 边形共有对角线 条.
总结:
多边形一般按边数命名,并用它各个顶点的字母顺次排列来表示.
四边形ABCD
五边形ABCDE
六边形ABCDEF
问题5 根据多边形边和顶点怎样命名它们呢?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
问题6 请同学们用量角器和直尺度量一下问题二中的三幅图片中的边和内角有什么不同?
多边形中,如果各条边都相等,各个内角都相等,这样的多边形叫做正多边形 .
图(1)(2)中的边和内角不全相等,图(3)的边和内角都相等
问题7 下列多边形是正多边形吗?如不是,请说明为什么?
(四条边都相等)
(四个角都相等)
都不是,第一个图形不符合四个角都相等;
第二个图形不符合各边都相等.
注意:判断一个多边形是不是正多边形,各边都相等,各角都相等,两个条件必须同时具备.
问题8 请分别画出下列两个图形各边所在的直线,你能得到什么结论?
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形就是凸多边形,如图(1).
而图(2)所示的图形就不是凸多边形.
(1)
(2)
本教科书中所研究的都是凸多边形.
A
B
C
D
A
B
C
D
探究
问题2 你知道长方形和正方形的内角和是多少度吗?
问题1 三角形的内角和是多少度?
三角形内角和是 180°.
都是 360°.
问题3 猜想任意四边形的内角和是多少度?
猜想:四边形 ABCD 的内角和是 360°.
问题4 你能用以前学过的知识证明一下你的结论吗?
A
B
C
D
如图,连接AC,能推得四边形的内角和吗
这里的AC是四边形ABCD的一条对角线.
四边形的内角和等于两个三角形内角和之和:
180°×2 = 360°
方法1:
该四边形被分成三个三角形,
所以四边形 ABCD 的内角和为
180°×3 - (∠AEB+∠AED+∠CED)
= 180°×3 - 180°
= 360°.
方法2:
如图,在 BC 边上任取一点 E,连接 AE,DE,能推得四边形内角和吗
A
B
C
D
E
方法3:
如图,在四边形内任取一点О,连接OA,OB,OC, OD,也能推得四边形内角和吗
四边形的内角和等于 4 个三角形内角和之和,减去一个圆周角:
180°×4 - 360° = 360°
A
B
C
D
E
A
B
C
D
P
如图,在四边形外任取一点 P,连接 PA、PB、PC、PD 将四边形变成有一个公共顶点的四个三角形.
所以四边形 ABCD 的内角和为
180°×3 - 180° = 360°.
结论: 四边形的内角和为360°.
方法4:
以上这四种方法都运用了转化的思想,把四边形分割成三角形,转化为已学的三角形内角和进行求解.
多边形的问题也可以通过添加辅助线转化为三角形问题来解决.
问题5 你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗
A
C
D
E
B
A
B
C
D
E
F
内角和为 180°×3 = 540°.
内角和为 180°×4 = 720°.
边数 图形 从多边形的一顶点引出的对角线条数 分割出的三角形个数 多边形内角和
三角形
四边形
五边形
六边形
···
n 边形
···
0
n - 3
1
2
3
1
2
3
4
n - 2
( n -2 )·180°
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
···
···
···
由特殊到一般
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
外部
转化思想
多边形的内角和公式
n 边形的内角和等于 (n - 2)×180°.
总结
小唯每跑完一圈,身体转过的角度之和是多少?
思考
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角. (如图所示:∠1,∠2,∠3,∠4,∠5)
在多边形的每个顶点处取一个外角,它们的和叫做多边形的外角和.
如图,在五边形的每个顶点处各取一个外角.
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:五个外角加上它们分别相邻的五个内角和是多少?
互补
5×180° = 900°
五边形的外角和
= 360°.
= 5个平角和
-五边形内角和
= 5×180°
-(5-2) × 180°
结论:五边形的外角和等于 360°.
问题3:这五个平角和与五边形的内角和、外角和有什么关系?
归纳
定理: n 边形的外角和等于 360°(n 为不小于 3 的整数).
注意:多边形的外角和与边数无关
问题4: 一个n边形的外角和是多少度?
五边形的外角和=180°×5-五边形内角和=360°
六边形的外角和=180°×6-六边形内角和=360°
问题5:你能推导出正n边形的内角与外角公式吗?
n 边形的内角和等于(n-2)·180°,所以
每个内角等于 ;
每个外角等于 .
正n边形的每个内角都相等,每个外角也都相等.
活动的铁栅栏门,正是由于四边形可以变动,所以它可以拉开,也可以收拢.
用来固定相机的三脚架,三角形不能变动,所以调整好高度就不会动了.
请你根据生活中的多边形讨论多边形的物体稳定吗?
讨论
三角形的三边一旦确定,其形状和大小就确定了,所以三角形具有稳定性;四边形各条边的长确定后,其形状不能确定,因此四边形具有不稳定性
归纳
1. 下列多边形中,不是凸多边形的是( )
A
B
C
D
B
随堂练习
2. 一个多边形从一个顶点可引对角线 3 条,这个多边形
的内角和等于( )
A. 360° B. 540° C. 720° D. 900°
C
4. 过八边形的一个顶点画对角线,把这个八边形分成 个三角形.
6
3.如图,将两个相同的正六边形螺母摆放在桌面上,则∠1的度数为____°.
60
6.已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
解:设这个多边形的内角为7x °,外角为2x°,
根据题意得:
7x+2x=180,
解得: x=20.
即每个内角是140 °,每个外角是40 °.
360÷40 °=9.
答:这个多边形是九边形.
7. 一个多边形的内角和为 1800°,截去一个角后,求得到的多边形的内角和.
解:∵ 1800÷180=10,
∴ 原多边形边数为10+2=12.
∵ 一个多边形截去一个内角后,边数可能减 1,可能不变,也可能加 1,
∴ 新多边形的边数可能是 11,12,13.
∴ 新多边形的内角和可能是 1620°,1800°,1980°.
能力提升:如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7 的度数.
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形的内角和
=540°.
8
9
多边形的概念
定义
在平面内,由若干条 同一条直线上的线段首尾顺次相接组成的封闭图形叫做多边形.
相关
概念
1. 叫做多边形的边.
2. 叫做多边形的顶点.
3. 叫做多边形的内角,简称多边形的角;
4. 叫做多边形的外角.
5. 叫做多边形的对角线 .
正多边形
如果 ,这样的多边形叫做正多边形 .
课堂小结
不在
组成多边形的线段
相邻两边的公共端点
多边形中相邻两边组成的角
在顶点处一边与另一边的延长线所组成的角
多边形中连接不相邻的两个顶点的线段,
各条边都相等,各个内角都相等
多边形的性质
内角和计算公式
(n - 2)×180°(n≥3,且为整数)
外角和
多边形的外角和等于 .
特别注意:与边数无关
正多边形
内角= ,外角=
四边形
具有
不稳定性
360°
