19.3.3 正方形课件 (共37张PPT)
文档属性
| 名称 | 19.3.3 正方形课件 (共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 17:03:05 | ||
图片预览




文档简介
(共37张PPT)
19.3.3 正方形
八年级下
沪科版
1. 理解正方形的概念,以及它与平行四边形、矩形、菱形之间的关系;
2. 能熟练运用正方形的性质和判定进行计算和证明.
学习目标
重点
难点
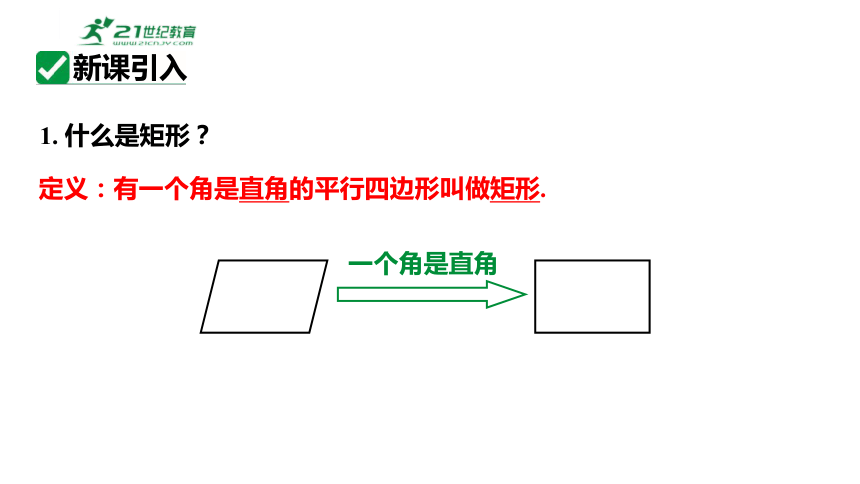
1. 什么是矩形?
定义:有一个角是直角的平行四边形叫做矩形.
一个角是直角
新课引入
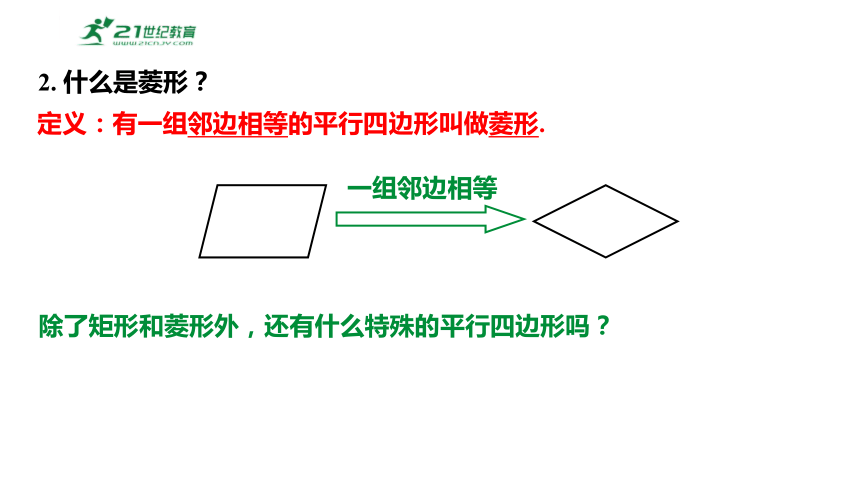
2. 什么是菱形?
定义:有一组邻边相等的平行四边形叫做菱形.
一组邻边相等
除了矩形和菱形外,还有什么特殊的平行四边形吗?
正方形是我们所熟悉的图形,如图是魔方的一个面.你认为正方形是本节所学的哪种图形的特例,为什么
一 正方形的性质
新知学习
矩 形
〃
〃
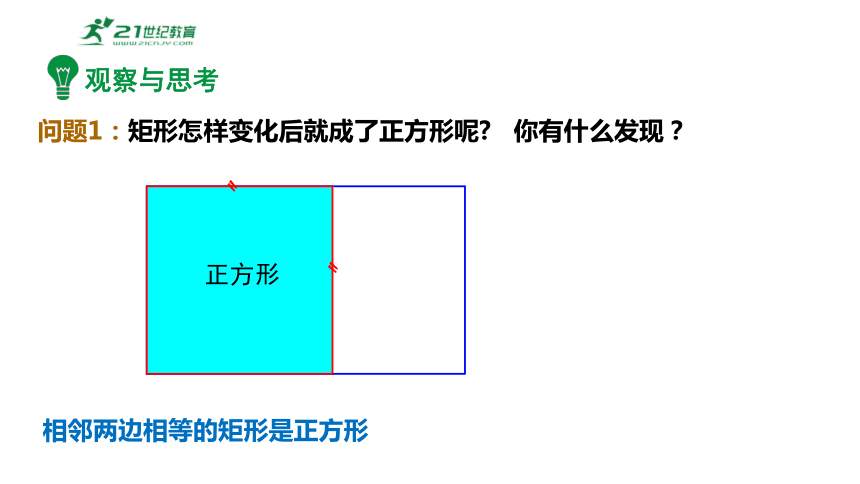
问题1:矩形怎样变化后就成了正方形呢 你有什么发现?
正方形
观察与思考
相邻两边相等的矩形是正方形
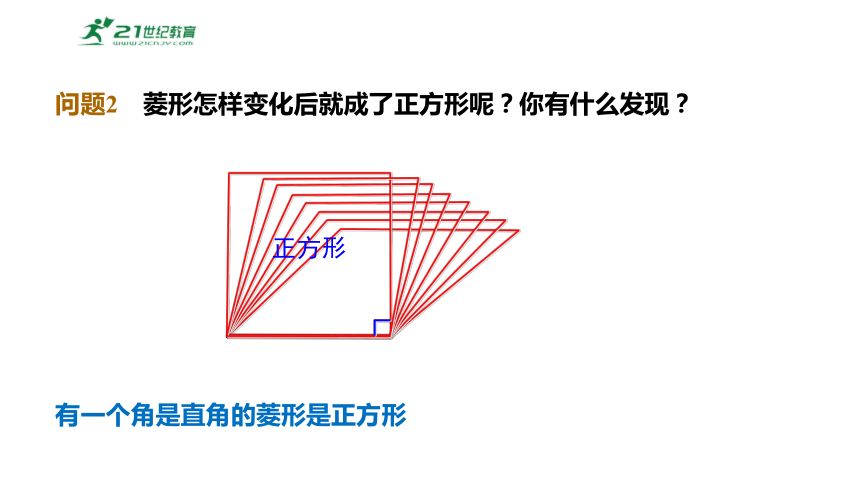
问题2 菱形怎样变化后就成了正方形呢?你有什么发现?
正方形
有一个角是直角的菱形是正方形
1.正方形的定义:
归纳
有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
两层含义
(1) 有一个角是直角的平行四边形 (矩形)
(2) 有一组邻边相等的平行四边形 (菱形)
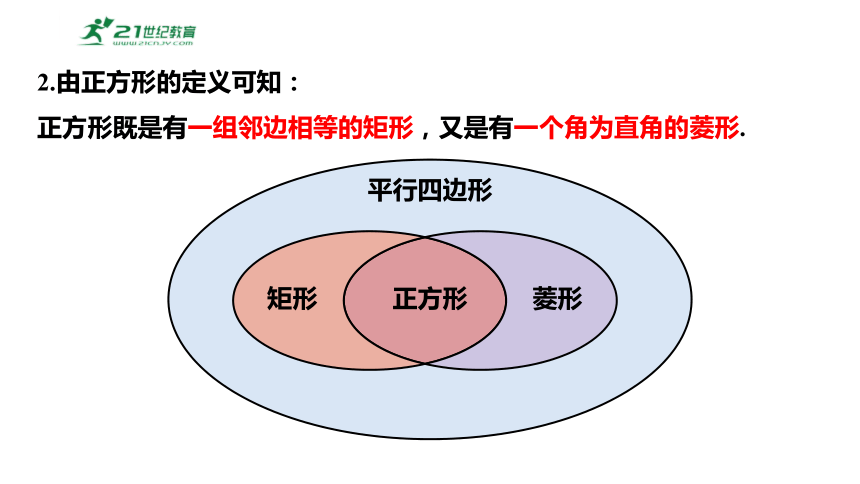
平行四边形
矩形
菱形
正方形
2.由正方形的定义可知:
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.
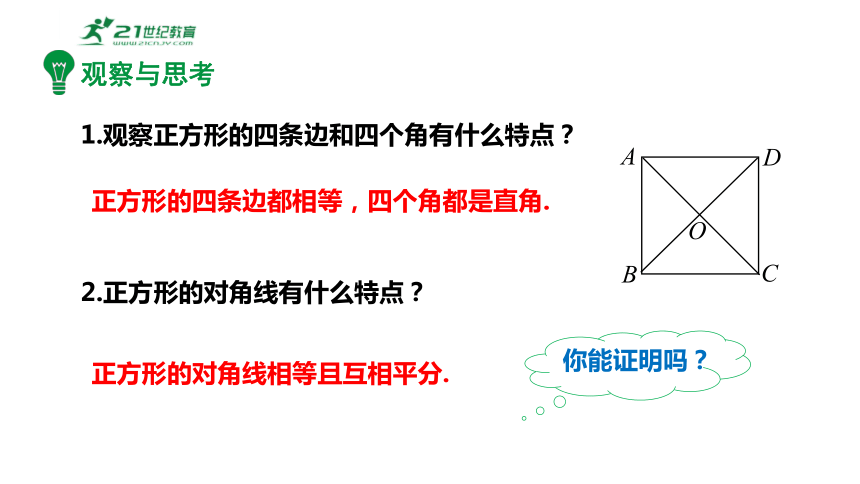
观察与思考
1.观察正方形的四条边和四个角有什么特点?
2.正方形的对角线有什么特点?
A
B
C
D
O
正方形的四条边都相等,四个角都是直角.
正方形的对角线相等且互相平分.
你能证明吗?
已知:如图,四边形 ABCD 是正方形.
求证:正方形 ABCD 四边相等,四个角都是直角.
A
B
C
D
证明:∵ 四边形 ABCD 是正方形.
∴∠A = 90°,AB = AD (正方形的定义).
又∵ 正方形是平行四边形,
∴ 正方形是矩形 (矩形的定义),
正方形是菱形 (菱形的定义).
∴∠A =∠B =∠C =∠D = 90°,
AB = BC = CD = AD.
正方形的四条边都相等,四个角都是直角.
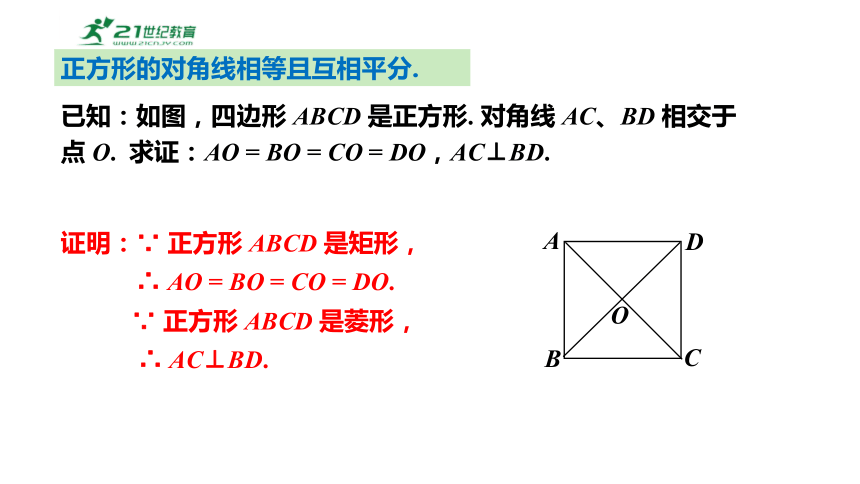
已知:如图,四边形 ABCD 是正方形. 对角线 AC、BD 相交于点 O. 求证:AO = BO = CO = DO,AC⊥BD.
A
B
C
D
O
证明:∵ 正方形 ABCD 是矩形,
∴ AO = BO = CO = DO.
∵ 正方形 ABCD 是菱形,
∴ AC⊥BD.
正方形的对角线相等且互相平分.
思考
正方形既是特殊的矩形,又是特殊的菱形.
正方形有哪些性质?
正方形具有矩形,菱形的所有性质.
归纳
正方形的性质
边
对边平行
四边相等
角
对角线
对角线相等且互相垂直平分
每条对角线平分一组对角
:四个角相等且都是直角
A
B
D
C
O
思考
正方形是中心对称图形吗?是轴对称图形吗?.
正方形既是中心对称图形,又是轴对称图形,它有4条对称轴.
A
B
C
D
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形 ABCD 是正方形,对角线 AC、BD 相交于点 O.
求证:△ABO、 △BCO、 △CDO、 △DAO 是全等的等腰直角三角形.
证明:∵四边形 ABCD 是正方形,
∴AC = BD,AC⊥BD,AO = CO = BO = DO
∴△ABO、△BCO、△CDO、△DAO 都是等腰直角三角形,
并且△ABO ≌△BCO ≌△CDO ≌△DAO.
图中共有多少个等腰直角三角形?
图中共有多少个等腰直角三角形?
8个,△ABO、△BCO、△CDO、△DAO、△ABD、△BCD、△ABC、△ACD.
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
二 正方形的判定
活动
已知:如图,在矩形 ABCD 中,AC,DB 是它的两条对
角线,AC⊥DB.
求证:四边形 ABCD 是正方形.
证明:∵ 四边形 ABCD 是矩形,
∴ AO = CO = BO = DO,∠ADC = 90°.
∵ AC⊥DB,
∴ AD = AB = BC = CD.
∴ 四边形 ABCD 是正方形.
对角线互相垂直的矩形是正方形.
A
B
C
D
O
证一证:
数学语言:
在矩形ABCD中, ∵ AC⊥BD,
∴四边形ABCD是正方形.
A
B
D
C
O
归纳
对角线互相垂直的矩形是正方形.
通过以上证明,我们得到正方形的一个判定:
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状,量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
已知:如图,在菱形 ABCD 中,对角线 AC = DB.
求证:四边形 ABCD 是正方形.
证明:∵ 四边形 ABCD 是菱形,
∴ AB = BC = CD = AD,AC⊥DB.
∵ AC = DB,
∴ AO = BO = CO = DO.
∴△AOD,△AOB,△COD,△BOC 是等腰直角三角形.
∴∠DAB =∠ABC =∠BCD =∠ADC = 90°.
∴ 四边形 ABCD 是正方形.
对角线相等的菱形是正方形.
A
B
C
D
O
证一证:
归纳
对角线相等的菱形是正方形.
通过以上证明,我们得到正方形的一个判定:
数学语言:
在菱形ABCD中, ∵ AC=BD,
∴四边形ABCD是正方形.
A
B
D
C
O
一个角是直角
或对角线相等
一组邻边相等
或对角线相互垂直
一组邻边相等
或对角线相互垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
对角线相等且互相垂直
归纳
正方形判定的几条途径
拓展
顺次连接菱形各边中点能得到怎样的特殊平行四边形?
顺次连接菱形各边中点得到正方形.
例 如图,点 A′,B′,C′,D′ 分别是正方形 ABCD 四条边上的点,并且 AA′ = BB′ = CC′ = DD′.
求证:四边形 A′B′C′D′ 是正方形.
证明 因为四边形ABCD是正方形,所以
AB = BC = CD = DA.
又∵ AA′ = BB′ = CC′ = DD′,
∴ D′A=A′B = B′C = C′D.
∵∠A=∠B=∠C=∠D= 90°,
∴△AA′D′ ≌ △BB′A′ ≌△CC′B′ ≌△DD′C′.
∴A′B′ = B′C′= C′D′= D′A′,
即四边形 A′B′C′D′ 是菱形.
又 ∵∠1=∠3,∠1+∠2= 90°,
∴∠2+∠3= 90°,
∴∠D′A′B′= 90°.
所以四边形 A′B′C′D′ 是正方形.
1.下列各句判定正方形的说法是否正确?
(1) 有一个角是直角的菱形是正方形. ( )
(2) 有一组邻边相等的矩形是正方形. ( )
(3) 对角线相等的菱形是正方形. ( )
(4) 对角线互相垂直的矩形是正方形. ( )
(5) 对角线相等且互相垂直的四边形是正方形. ( )
√
√
√
√
×
对角线相等且互相垂直平分的四边形是正方形.
随堂练习
2.如图,是小明家客厅地面铺设的瓷砖图案,其中四边形ABCD是正方形,阴影部分是四个全等的菱形.已知菱形的两条对角线长分别为48 cm,20 cm,则图中空白部分的面积为_______cm2.
2688
3. 已知:如图,在△ABC中,AB=AC,D是BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC 边的中点,
∴BD=CD,
∴△BED≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,
∴四边形DFAE是矩形.
∵△BED≌△CFD,
∴DE=DF,∴矩形DFAE是正方形.
(2)若∠A=90°,求证:四边形DFAE是正方形.
证明:PN⊥l1,QM⊥l1,
∴∠PNM =∠QMN = 90°,
∴∠PNM +∠OMN = 180°,
∴PN∥QM.
∵l1∥l2,即 PQ∥NM,
∴四边形 POMN 是矩形.
4.已知:如图,四边形ABCD是正方形,分别过点A、C两点l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点
求证:四边形PQMN是正方形.
∵四边形 ABCD 是正方形,
∴∠BAD =∠ADC = 90°,AB = AD = DC,
∴∠BAM +∠DAN = 90°.
又∠AND +∠DAN = 90°,
∴∠BAM =∠ADN.
∴△BAM ≌△ADN (AAS) .
∴AM = DN. 同理可证 AN = DP.
∴AM + AN = DN + DP,即 MN = PN.
∴四边形 PQMN 是正方形.
总结:先证出四边形PQMN 是矩形,再证明一组邻边相等 (MN = NP).
1. 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
2. 正方形既是特殊的矩形,又是特殊的菱形. 具有矩形,菱形的所有性质.
正方形的性质
边
对边平行
四边相等
角
对角线
对角线相等且互相垂直平分
每条对角线平分一组对角
:四个角相等且都是直角
课堂小结
3. 正方形的判定.
一个角是直角
或对角线相等
一组邻边相等
或对角线相互垂直
一组邻边相等
或对角线相互垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
对角线相等且互相垂直
19.3.3 正方形
八年级下
沪科版
1. 理解正方形的概念,以及它与平行四边形、矩形、菱形之间的关系;
2. 能熟练运用正方形的性质和判定进行计算和证明.
学习目标
重点
难点
1. 什么是矩形?
定义:有一个角是直角的平行四边形叫做矩形.
一个角是直角
新课引入
2. 什么是菱形?
定义:有一组邻边相等的平行四边形叫做菱形.
一组邻边相等
除了矩形和菱形外,还有什么特殊的平行四边形吗?
正方形是我们所熟悉的图形,如图是魔方的一个面.你认为正方形是本节所学的哪种图形的特例,为什么
一 正方形的性质
新知学习
矩 形
〃
〃
问题1:矩形怎样变化后就成了正方形呢 你有什么发现?
正方形
观察与思考
相邻两边相等的矩形是正方形
问题2 菱形怎样变化后就成了正方形呢?你有什么发现?
正方形
有一个角是直角的菱形是正方形
1.正方形的定义:
归纳
有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
两层含义
(1) 有一个角是直角的平行四边形 (矩形)
(2) 有一组邻边相等的平行四边形 (菱形)
平行四边形
矩形
菱形
正方形
2.由正方形的定义可知:
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.
观察与思考
1.观察正方形的四条边和四个角有什么特点?
2.正方形的对角线有什么特点?
A
B
C
D
O
正方形的四条边都相等,四个角都是直角.
正方形的对角线相等且互相平分.
你能证明吗?
已知:如图,四边形 ABCD 是正方形.
求证:正方形 ABCD 四边相等,四个角都是直角.
A
B
C
D
证明:∵ 四边形 ABCD 是正方形.
∴∠A = 90°,AB = AD (正方形的定义).
又∵ 正方形是平行四边形,
∴ 正方形是矩形 (矩形的定义),
正方形是菱形 (菱形的定义).
∴∠A =∠B =∠C =∠D = 90°,
AB = BC = CD = AD.
正方形的四条边都相等,四个角都是直角.
已知:如图,四边形 ABCD 是正方形. 对角线 AC、BD 相交于点 O. 求证:AO = BO = CO = DO,AC⊥BD.
A
B
C
D
O
证明:∵ 正方形 ABCD 是矩形,
∴ AO = BO = CO = DO.
∵ 正方形 ABCD 是菱形,
∴ AC⊥BD.
正方形的对角线相等且互相平分.
思考
正方形既是特殊的矩形,又是特殊的菱形.
正方形有哪些性质?
正方形具有矩形,菱形的所有性质.
归纳
正方形的性质
边
对边平行
四边相等
角
对角线
对角线相等且互相垂直平分
每条对角线平分一组对角
:四个角相等且都是直角
A
B
D
C
O
思考
正方形是中心对称图形吗?是轴对称图形吗?.
正方形既是中心对称图形,又是轴对称图形,它有4条对称轴.
A
B
C
D
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形 ABCD 是正方形,对角线 AC、BD 相交于点 O.
求证:△ABO、 △BCO、 △CDO、 △DAO 是全等的等腰直角三角形.
证明:∵四边形 ABCD 是正方形,
∴AC = BD,AC⊥BD,AO = CO = BO = DO
∴△ABO、△BCO、△CDO、△DAO 都是等腰直角三角形,
并且△ABO ≌△BCO ≌△CDO ≌△DAO.
图中共有多少个等腰直角三角形?
图中共有多少个等腰直角三角形?
8个,△ABO、△BCO、△CDO、△DAO、△ABD、△BCD、△ABC、△ACD.
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
二 正方形的判定
活动
已知:如图,在矩形 ABCD 中,AC,DB 是它的两条对
角线,AC⊥DB.
求证:四边形 ABCD 是正方形.
证明:∵ 四边形 ABCD 是矩形,
∴ AO = CO = BO = DO,∠ADC = 90°.
∵ AC⊥DB,
∴ AD = AB = BC = CD.
∴ 四边形 ABCD 是正方形.
对角线互相垂直的矩形是正方形.
A
B
C
D
O
证一证:
数学语言:
在矩形ABCD中, ∵ AC⊥BD,
∴四边形ABCD是正方形.
A
B
D
C
O
归纳
对角线互相垂直的矩形是正方形.
通过以上证明,我们得到正方形的一个判定:
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状,量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
已知:如图,在菱形 ABCD 中,对角线 AC = DB.
求证:四边形 ABCD 是正方形.
证明:∵ 四边形 ABCD 是菱形,
∴ AB = BC = CD = AD,AC⊥DB.
∵ AC = DB,
∴ AO = BO = CO = DO.
∴△AOD,△AOB,△COD,△BOC 是等腰直角三角形.
∴∠DAB =∠ABC =∠BCD =∠ADC = 90°.
∴ 四边形 ABCD 是正方形.
对角线相等的菱形是正方形.
A
B
C
D
O
证一证:
归纳
对角线相等的菱形是正方形.
通过以上证明,我们得到正方形的一个判定:
数学语言:
在菱形ABCD中, ∵ AC=BD,
∴四边形ABCD是正方形.
A
B
D
C
O
一个角是直角
或对角线相等
一组邻边相等
或对角线相互垂直
一组邻边相等
或对角线相互垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
对角线相等且互相垂直
归纳
正方形判定的几条途径
拓展
顺次连接菱形各边中点能得到怎样的特殊平行四边形?
顺次连接菱形各边中点得到正方形.
例 如图,点 A′,B′,C′,D′ 分别是正方形 ABCD 四条边上的点,并且 AA′ = BB′ = CC′ = DD′.
求证:四边形 A′B′C′D′ 是正方形.
证明 因为四边形ABCD是正方形,所以
AB = BC = CD = DA.
又∵ AA′ = BB′ = CC′ = DD′,
∴ D′A=A′B = B′C = C′D.
∵∠A=∠B=∠C=∠D= 90°,
∴△AA′D′ ≌ △BB′A′ ≌△CC′B′ ≌△DD′C′.
∴A′B′ = B′C′= C′D′= D′A′,
即四边形 A′B′C′D′ 是菱形.
又 ∵∠1=∠3,∠1+∠2= 90°,
∴∠2+∠3= 90°,
∴∠D′A′B′= 90°.
所以四边形 A′B′C′D′ 是正方形.
1.下列各句判定正方形的说法是否正确?
(1) 有一个角是直角的菱形是正方形. ( )
(2) 有一组邻边相等的矩形是正方形. ( )
(3) 对角线相等的菱形是正方形. ( )
(4) 对角线互相垂直的矩形是正方形. ( )
(5) 对角线相等且互相垂直的四边形是正方形. ( )
√
√
√
√
×
对角线相等且互相垂直平分的四边形是正方形.
随堂练习
2.如图,是小明家客厅地面铺设的瓷砖图案,其中四边形ABCD是正方形,阴影部分是四个全等的菱形.已知菱形的两条对角线长分别为48 cm,20 cm,则图中空白部分的面积为_______cm2.
2688
3. 已知:如图,在△ABC中,AB=AC,D是BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC 边的中点,
∴BD=CD,
∴△BED≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,
∴四边形DFAE是矩形.
∵△BED≌△CFD,
∴DE=DF,∴矩形DFAE是正方形.
(2)若∠A=90°,求证:四边形DFAE是正方形.
证明:PN⊥l1,QM⊥l1,
∴∠PNM =∠QMN = 90°,
∴∠PNM +∠OMN = 180°,
∴PN∥QM.
∵l1∥l2,即 PQ∥NM,
∴四边形 POMN 是矩形.
4.已知:如图,四边形ABCD是正方形,分别过点A、C两点l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点
求证:四边形PQMN是正方形.
∵四边形 ABCD 是正方形,
∴∠BAD =∠ADC = 90°,AB = AD = DC,
∴∠BAM +∠DAN = 90°.
又∠AND +∠DAN = 90°,
∴∠BAM =∠ADN.
∴△BAM ≌△ADN (AAS) .
∴AM = DN. 同理可证 AN = DP.
∴AM + AN = DN + DP,即 MN = PN.
∴四边形 PQMN 是正方形.
总结:先证出四边形PQMN 是矩形,再证明一组邻边相等 (MN = NP).
1. 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
2. 正方形既是特殊的矩形,又是特殊的菱形. 具有矩形,菱形的所有性质.
正方形的性质
边
对边平行
四边相等
角
对角线
对角线相等且互相垂直平分
每条对角线平分一组对角
:四个角相等且都是直角
课堂小结
3. 正方形的判定.
一个角是直角
或对角线相等
一组邻边相等
或对角线相互垂直
一组邻边相等
或对角线相互垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
对角线相等且互相垂直
