20.1数据的频数分布 课件(共24张PPT)
文档属性
| 名称 | 20.1数据的频数分布 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 982.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 17:03:05 | ||
图片预览







文档简介
(共24张PPT)
20.1 数据的频数分布
八年级下
沪科版
1.理解频数、频率等概念,会对一组数据进行统计,列出相应的频数分布表,并制作频数直方图.
2.能根据统计结果作出合理的判断和预测,并能解决简单的实际问题,体会统计对决策的作用.
学习目标
重点
难点
我们学习过哪几种统计图,它们在描述数据时分别具有怎样的特点?
条形统计图 (表示每个项目的具体数目)
扇形统计图 (表示各部分在总体中所占的百分比)
折线统计图 (反映事物的变化趋势)
有了上述这些方法是否就能够处理所有关于数据的工作了呢?
新课引入
问题1 某校学生在假期进行“空气质量调查”的课题研究时,他们从当地的气象部门提供的今年上半年的资料中,随意抽取30天的空气综合污染指数,数据如下:
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
新知学习
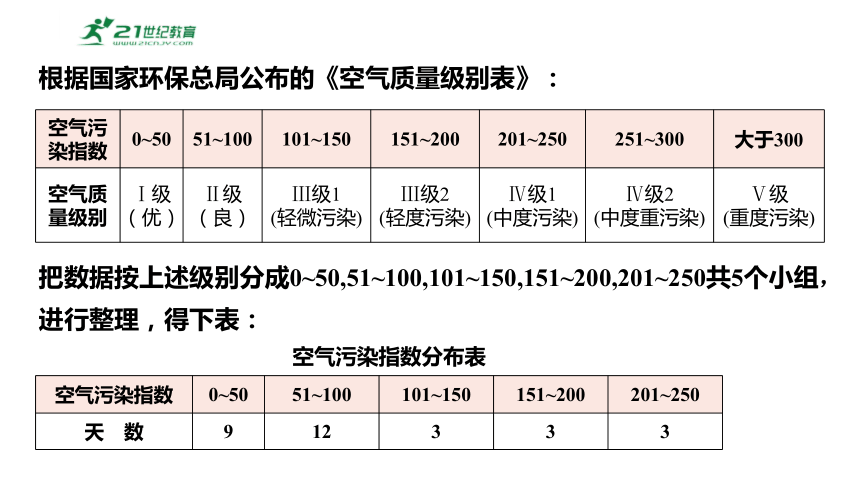
根据国家环保总局公布的《空气质量级别表》:
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级 (优) Ⅱ级 (良) Ⅲ级1 (轻微污染) Ⅲ级2 (轻度污染) Ⅳ级1 (中度污染) Ⅳ级2 (中度重污染) Ⅴ级
(重度污染)
把数据按上述级别分成0~50,51~100,101~150,151~200,201~250共5个小组,进行整理,得下表:
空气污染指数 0~50 51~100 101~150 151~200 201~250
天 数 9 12 3 3 3
空气污染指数分布表
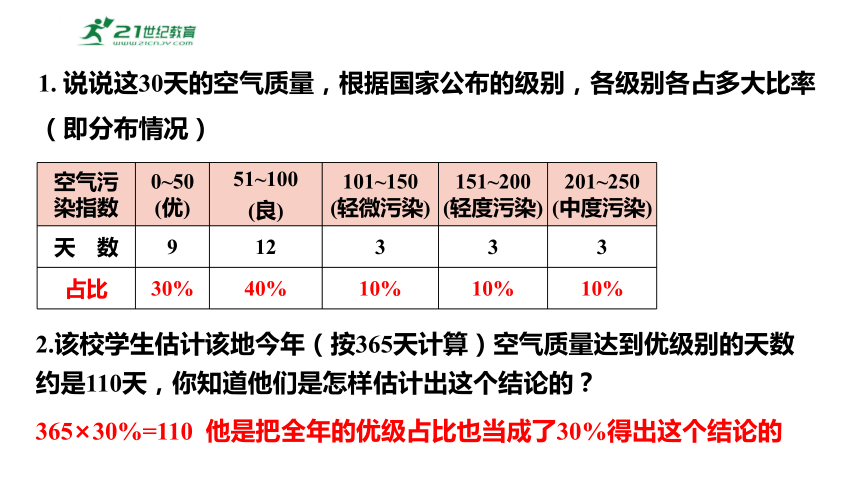
1. 说说这30天的空气质量,根据国家公布的级别,各级别各占多大比率(即分布情况)
2.该校学生估计该地今年(按365天计算)空气质量达到优级别的天数约是110天,你知道他们是怎样估计出这个结论的?
空气污染指数 0~50(优) 51~100 (良) 101~150(轻微污染) 151~200(轻度污染) 201~250(中度污染)
天 数 9 12 3 3 3
占比 30% 40% 10% 10% 10%
365×30%=110 他是把全年的优级占比也当成了30%得出这个结论的
启示我们:面对量大的数据,要想从中获取所需信息,常常先要选择好合适的统计表、图.把相差不大的数据放在一起,进行适当分组(例如,这里按空气质量级别分组),然后统计出落在各个小组内数据的个数,并借助表格将分组结果及各组数据的个数进行整理,这样,便反映出这批数据的分布规律.
3.前面分析数据分布的方法能够给我们什么启发?
问题2 某校体卫组想对该校八年级全体学生一周内平均每天参加课外锻炼的时间(单位:min)有所了解,从中随机抽査了40名学生,结果如下
40, 21 , 35, 24, 40, 38, 23, 52, 35, 62,
36, 15, 51, 45, 42, 40, 32, 43, 36, 34,
53, 38, 40, 39, 32, 45, 40, 50, 45, 40,
50, 26, 45, 40, 45, 35, 40, 42, 45, 40.
为了解这批数据反映的情况,可以对它进行怎样的分析呢?
(1)计算这批数据中的最大数与最小数的差.
数据中的最大数:62
数据中的最小数:15
两者之差为:62-15=47
由此可知这组数据的变动范围
说明每天参加课外锻炼的时间变化范围是47.
(2)决定组距和组数.
组距是指每个小组的两个端点间的距离.将这批数据分组.如果每组组距相同,并取组距为8 ,那么
组数=
即把数据分成 6 组.
注意:这里组数算出来是小于6的分数,因此要将数据分成6组.
这里组数和组距分别是6和8.
(3)决定分点.
将数据按照8min的组距分组,从15开始分成15~23,23~31,31~39,39~47,47~55,55~63这6组,我们发现数据23,39正好落在分点上,不好决定他们究竟属于哪一组
为了避免数据落在分点上,一般地把表示分点的数比原数据多取一位小数,并把第一组的起点定为比最小的数据稍小一点的数.
如把第一组的起点定为14.5,这样所分的6个组是:
14.5~22.5, 22.5~30.5, 30.5~38.5,
38.5~46.5, 46.5~54.4, 54.5~62.5
(4)列频数分布表.
我们把一批数据中落在某个小组内数据的个数称为这个组的频数
通常用选举时唱票的方法,对落在各个小组内的数据个数进行记录,
算出每一个小组的频数,并制成频数分布表.
如果一批数据共有n个,而其中某一组数据是m个,那么 就是该组数据在这批数据中出现的频率.
40 名学生平均每天锻炼时间频数分布表
分组 频数统计 频数
14.5~22.5 2
22.5~30.5 3
30.5~38.5 10
38.5~46.5 19
46.5~54.5 5
54.5~62.5 1
合计 40
分组时,要注意使每个数据只落在一个组内,各小组的频数之
和等于数据总数.
(5)画频数直方图.
画出相互垂直的两条直线,用横轴表示分组情况,纵轴表示频数,绘出相应的长方形条,就得到了频数直方图.
频数直方图与前面所学的条形统计图比较相似,两者有什么区别和联系?
思考
(1)联系——用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况.
例 某校从七年级中任意抽取一个班,该班学生身高(单位:cm)的频数分布如表所示:
分组 136.5~141.5 141.5~146.5 146.5~151.5 151.5~156.5 156.5~161.5 161.5~166.5 166.5~171.5 171.5~176.5 合计
频数 1 4 10 15 9 8 2 1 50
根据所给表回答:
(1)身高在161.5cm以上的学生有多少?占全班人数的百分之几?
(2)估计该校七年级全体400名新生中,身高161.5cm以上的约有多少人?
解:(1)身高在161.5cm以上的学生有
8+2+1=11(人)
占全班人数的22%
(2)估计该校七年级全体400名新生中,身高161.5cm
以上的约有 400×22%=88(人)
分组 136.5~141.5 141.5~146.5 146.5~151.5 151.5~156.5 156.5~161.5 161.5~166.5 166.5~171.5 171.5~176.5 合计
频数 1 4 10 15 9 8 2 1 50
(1)计算这批数据中的最大数与最小数的差.
(2)决定组距和组数.
(3)决定分点.
(4)列频数分布表.
(5)画频数直方图.
数据处理的一般步骤:
归纳
1.一次数学测试后,某班 40 名学生的成绩被分为 5 组,第 1~4 组的频数分别为 12,10,6,8,则第 5 组的频率是( )
A.0.1
B.0.2
C.0.3
D.0.4
A
随堂练习
第5组的频数:40-12-10-6-8=4
第五组的频率: =0.1
2.如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元 B.10~15元
C.15~20元 D.20~25元
C
3.中学生每天的睡眠时间应不少于8小时.某校为了解学生每天的睡眠时长,随机抽取了部分学生进行调查,并将调查结果整理成如下的频数直方图,若该校有800名学生,则睡眠时间不足的学生有_______人.
320
4.为了解某中学九年级300名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果(单位: cm)如下:
175 161 171 176 167 181 161 173 171 177
179 172 165 157 173 173 166 177 169 181
下表是根据上述数据填写的表格的一部分.
(1)请填写表中未完成的部分;
(2)该校九年级男学生身高在171.5 cm~176.5 cm范围内的人数为多少?
6
25%
(2)解:300×30%=90(人)
∴该校九年级男学生身高在171.5 cm~176.5 cm范围内的人数为90人.
(1)计算这批数据中的最大数与最小数的差.
(2)决定组距和组数.
(3)决定分点.
(4)列频数分布表.
(5)画频数直方图.
数据处理的一般步骤:
课堂小结
20.1 数据的频数分布
八年级下
沪科版
1.理解频数、频率等概念,会对一组数据进行统计,列出相应的频数分布表,并制作频数直方图.
2.能根据统计结果作出合理的判断和预测,并能解决简单的实际问题,体会统计对决策的作用.
学习目标
重点
难点
我们学习过哪几种统计图,它们在描述数据时分别具有怎样的特点?
条形统计图 (表示每个项目的具体数目)
扇形统计图 (表示各部分在总体中所占的百分比)
折线统计图 (反映事物的变化趋势)
有了上述这些方法是否就能够处理所有关于数据的工作了呢?
新课引入
问题1 某校学生在假期进行“空气质量调查”的课题研究时,他们从当地的气象部门提供的今年上半年的资料中,随意抽取30天的空气综合污染指数,数据如下:
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
新知学习
根据国家环保总局公布的《空气质量级别表》:
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级 (优) Ⅱ级 (良) Ⅲ级1 (轻微污染) Ⅲ级2 (轻度污染) Ⅳ级1 (中度污染) Ⅳ级2 (中度重污染) Ⅴ级
(重度污染)
把数据按上述级别分成0~50,51~100,101~150,151~200,201~250共5个小组,进行整理,得下表:
空气污染指数 0~50 51~100 101~150 151~200 201~250
天 数 9 12 3 3 3
空气污染指数分布表
1. 说说这30天的空气质量,根据国家公布的级别,各级别各占多大比率(即分布情况)
2.该校学生估计该地今年(按365天计算)空气质量达到优级别的天数约是110天,你知道他们是怎样估计出这个结论的?
空气污染指数 0~50(优) 51~100 (良) 101~150(轻微污染) 151~200(轻度污染) 201~250(中度污染)
天 数 9 12 3 3 3
占比 30% 40% 10% 10% 10%
365×30%=110 他是把全年的优级占比也当成了30%得出这个结论的
启示我们:面对量大的数据,要想从中获取所需信息,常常先要选择好合适的统计表、图.把相差不大的数据放在一起,进行适当分组(例如,这里按空气质量级别分组),然后统计出落在各个小组内数据的个数,并借助表格将分组结果及各组数据的个数进行整理,这样,便反映出这批数据的分布规律.
3.前面分析数据分布的方法能够给我们什么启发?
问题2 某校体卫组想对该校八年级全体学生一周内平均每天参加课外锻炼的时间(单位:min)有所了解,从中随机抽査了40名学生,结果如下
40, 21 , 35, 24, 40, 38, 23, 52, 35, 62,
36, 15, 51, 45, 42, 40, 32, 43, 36, 34,
53, 38, 40, 39, 32, 45, 40, 50, 45, 40,
50, 26, 45, 40, 45, 35, 40, 42, 45, 40.
为了解这批数据反映的情况,可以对它进行怎样的分析呢?
(1)计算这批数据中的最大数与最小数的差.
数据中的最大数:62
数据中的最小数:15
两者之差为:62-15=47
由此可知这组数据的变动范围
说明每天参加课外锻炼的时间变化范围是47.
(2)决定组距和组数.
组距是指每个小组的两个端点间的距离.将这批数据分组.如果每组组距相同,并取组距为8 ,那么
组数=
即把数据分成 6 组.
注意:这里组数算出来是小于6的分数,因此要将数据分成6组.
这里组数和组距分别是6和8.
(3)决定分点.
将数据按照8min的组距分组,从15开始分成15~23,23~31,31~39,39~47,47~55,55~63这6组,我们发现数据23,39正好落在分点上,不好决定他们究竟属于哪一组
为了避免数据落在分点上,一般地把表示分点的数比原数据多取一位小数,并把第一组的起点定为比最小的数据稍小一点的数.
如把第一组的起点定为14.5,这样所分的6个组是:
14.5~22.5, 22.5~30.5, 30.5~38.5,
38.5~46.5, 46.5~54.4, 54.5~62.5
(4)列频数分布表.
我们把一批数据中落在某个小组内数据的个数称为这个组的频数
通常用选举时唱票的方法,对落在各个小组内的数据个数进行记录,
算出每一个小组的频数,并制成频数分布表.
如果一批数据共有n个,而其中某一组数据是m个,那么 就是该组数据在这批数据中出现的频率.
40 名学生平均每天锻炼时间频数分布表
分组 频数统计 频数
14.5~22.5 2
22.5~30.5 3
30.5~38.5 10
38.5~46.5 19
46.5~54.5 5
54.5~62.5 1
合计 40
分组时,要注意使每个数据只落在一个组内,各小组的频数之
和等于数据总数.
(5)画频数直方图.
画出相互垂直的两条直线,用横轴表示分组情况,纵轴表示频数,绘出相应的长方形条,就得到了频数直方图.
频数直方图与前面所学的条形统计图比较相似,两者有什么区别和联系?
思考
(1)联系——用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况.
例 某校从七年级中任意抽取一个班,该班学生身高(单位:cm)的频数分布如表所示:
分组 136.5~141.5 141.5~146.5 146.5~151.5 151.5~156.5 156.5~161.5 161.5~166.5 166.5~171.5 171.5~176.5 合计
频数 1 4 10 15 9 8 2 1 50
根据所给表回答:
(1)身高在161.5cm以上的学生有多少?占全班人数的百分之几?
(2)估计该校七年级全体400名新生中,身高161.5cm以上的约有多少人?
解:(1)身高在161.5cm以上的学生有
8+2+1=11(人)
占全班人数的22%
(2)估计该校七年级全体400名新生中,身高161.5cm
以上的约有 400×22%=88(人)
分组 136.5~141.5 141.5~146.5 146.5~151.5 151.5~156.5 156.5~161.5 161.5~166.5 166.5~171.5 171.5~176.5 合计
频数 1 4 10 15 9 8 2 1 50
(1)计算这批数据中的最大数与最小数的差.
(2)决定组距和组数.
(3)决定分点.
(4)列频数分布表.
(5)画频数直方图.
数据处理的一般步骤:
归纳
1.一次数学测试后,某班 40 名学生的成绩被分为 5 组,第 1~4 组的频数分别为 12,10,6,8,则第 5 组的频率是( )
A.0.1
B.0.2
C.0.3
D.0.4
A
随堂练习
第5组的频数:40-12-10-6-8=4
第五组的频率: =0.1
2.如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元 B.10~15元
C.15~20元 D.20~25元
C
3.中学生每天的睡眠时间应不少于8小时.某校为了解学生每天的睡眠时长,随机抽取了部分学生进行调查,并将调查结果整理成如下的频数直方图,若该校有800名学生,则睡眠时间不足的学生有_______人.
320
4.为了解某中学九年级300名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果(单位: cm)如下:
175 161 171 176 167 181 161 173 171 177
179 172 165 157 173 173 166 177 169 181
下表是根据上述数据填写的表格的一部分.
(1)请填写表中未完成的部分;
(2)该校九年级男学生身高在171.5 cm~176.5 cm范围内的人数为多少?
6
25%
(2)解:300×30%=90(人)
∴该校九年级男学生身高在171.5 cm~176.5 cm范围内的人数为90人.
(1)计算这批数据中的最大数与最小数的差.
(2)决定组距和组数.
(3)决定分点.
(4)列频数分布表.
(5)画频数直方图.
数据处理的一般步骤:
课堂小结
