16.2.2分式的加减 课件(共29张PPT)
文档属性
| 名称 | 16.2.2分式的加减 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 18:04:33 | ||
图片预览







文档简介
(共29张PPT)
16.2.2 分式的加减
八年级下
华师版
1.掌握分式的加减运算法则并运用其进行计算.
2.能够进行同分母和异分母的分式加减法运算.
3.理解分式的混合运算顺序,并能正确进行分式的混合运算.
重点
学习目标
难点
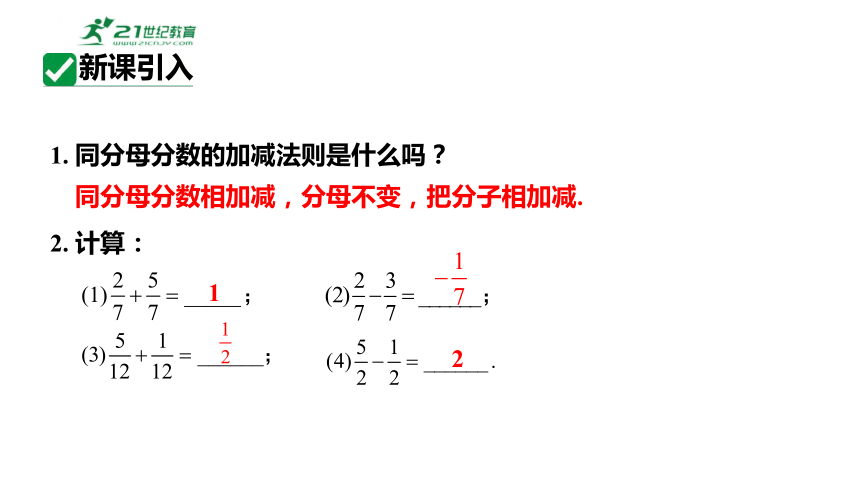
新课引入
1. 同分母分数的加减法则是什么吗?
1
2. 计算:
2
同分母分数相加减,分母不变,把分子相加减.
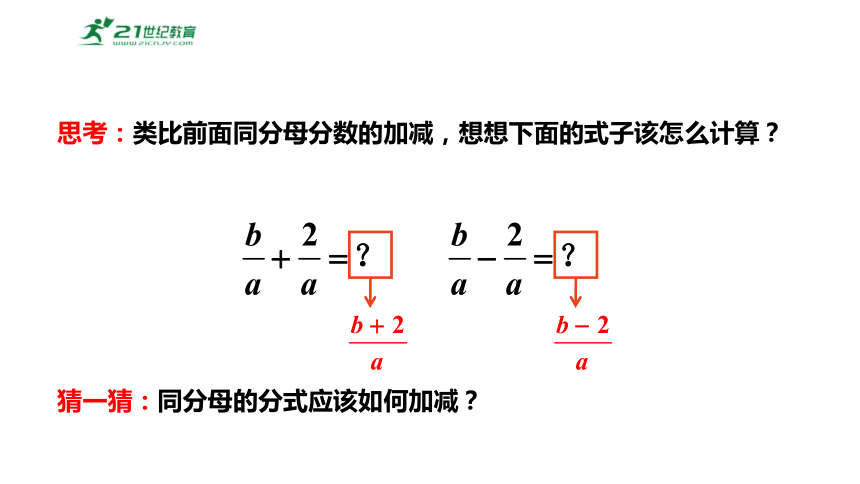
思考:类比前面同分母分数的加减,想想下面的式子该怎么计算?
猜一猜:同分母的分式应该如何加减?
同分母的分式相加减,分母不变,分子相加减.
上述法则可用式子表示为:
一、同分母分式的加减
新知学习
计算:
例1
解:
方法总结:
如果所得结果不是最简分式,应该通过约分进行化简.
解:(1)原式
例2 计算:
(2)
解:(2)
温馨提示
分母相同,而分子是多项式,分子相加减时要把分子看作一个整体,先用括号括起来,再进行加减,能分解因式的要先分解因式,最后结果要进行约分化简.
解:
例3 计算:
方法总结:
分母互为相反数时,要先化为同分母分式,再进行计算.
问题:
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数的加减
异分母分数相加减,先通分,
变为同分母的分数,再加减.
请思考 ( ), ( ).
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
类比:异分母的分式应该如何加减
异分母的分式相加减,先通分,变为同分母的分式,然后再加减.
上述法则可用式子表示为:
二、异分母分式的加减
分析:这里两个分式的分母不同,要先通分.为此,先找出它们的最简公分母.注意到x2-16=(x+4)(x-4),所以最简公分母是(x+4)(x-4).
计算:
例4
解:
例5 计算:
解:原式
解:原式
温馨提示
当分子、分母是多项式时,首先要进行因式分解;如果计算结果不是最简的,一定要进行约分将其化为最简分式或整式.
计算:
例6
解:原式
方法总结:
分式与整式相加减时,可把整式部分看成分母为1的式子,然后进行异分母分式的加减.
分式加减运算的一般步骤:
(1)将分母进行因式分解,确定最简公分母;
(2)通分,将异分母分式化为同分母分式;
(3)分母不变,分子相加减;
(4)整理分子成积的形式
(5)约分,化为最简分式或整式
方法总结
三、分式的混合运算
例7:计算
算乘方,除法变乘法.
约分,做乘法.
同分母分式相减.
解:原式=
计算
解:原式=
通分,除法变乘法.
约分,去括号.
乘方,因式分解.
1. 观察运算类型.
2. 确定运算顺序:
①先乘方,再乘除,最后加减,有括号要先算括号里面的.
②识别出能因式分解的多项式,并知道何时需要因式分解.
3. 书写计算过程:书写清晰,不跳步.
温馨提示
四、分式的化简求值
例8 先化简 ,再求值: ,其中 .
解:原式=
当 时,原式
解:原式
解:原式
随堂练习
1.计算:
解:原式
解:原式
解:原式
解:
2.混合运算:
(2)
解:原式
解:原式
当a= +1时,原式= +1-1= .
3. 先化简,再求值 :(1- ) ÷ ,其中a= +1.
1.同分母的分式相加减,分母不变,分子相加减.
2.异分母的分式相加减,先通分,变为同分母的分式,然后再加减.
1.分式的分子和分母是多项式时,在进行运算时要适时添加括号
2.整式和分式之间进行加减运算时,则要把整式看成分母是1的分式,以便通分
3.异分母分式进行加减运算需要先通分,关键是确定最简公分母
分式的加减
注意
加减法运算
课堂小结
16.2.2 分式的加减
八年级下
华师版
1.掌握分式的加减运算法则并运用其进行计算.
2.能够进行同分母和异分母的分式加减法运算.
3.理解分式的混合运算顺序,并能正确进行分式的混合运算.
重点
学习目标
难点
新课引入
1. 同分母分数的加减法则是什么吗?
1
2. 计算:
2
同分母分数相加减,分母不变,把分子相加减.
思考:类比前面同分母分数的加减,想想下面的式子该怎么计算?
猜一猜:同分母的分式应该如何加减?
同分母的分式相加减,分母不变,分子相加减.
上述法则可用式子表示为:
一、同分母分式的加减
新知学习
计算:
例1
解:
方法总结:
如果所得结果不是最简分式,应该通过约分进行化简.
解:(1)原式
例2 计算:
(2)
解:(2)
温馨提示
分母相同,而分子是多项式,分子相加减时要把分子看作一个整体,先用括号括起来,再进行加减,能分解因式的要先分解因式,最后结果要进行约分化简.
解:
例3 计算:
方法总结:
分母互为相反数时,要先化为同分母分式,再进行计算.
问题:
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数的加减
异分母分数相加减,先通分,
变为同分母的分数,再加减.
请思考 ( ), ( ).
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
类比:异分母的分式应该如何加减
异分母的分式相加减,先通分,变为同分母的分式,然后再加减.
上述法则可用式子表示为:
二、异分母分式的加减
分析:这里两个分式的分母不同,要先通分.为此,先找出它们的最简公分母.注意到x2-16=(x+4)(x-4),所以最简公分母是(x+4)(x-4).
计算:
例4
解:
例5 计算:
解:原式
解:原式
温馨提示
当分子、分母是多项式时,首先要进行因式分解;如果计算结果不是最简的,一定要进行约分将其化为最简分式或整式.
计算:
例6
解:原式
方法总结:
分式与整式相加减时,可把整式部分看成分母为1的式子,然后进行异分母分式的加减.
分式加减运算的一般步骤:
(1)将分母进行因式分解,确定最简公分母;
(2)通分,将异分母分式化为同分母分式;
(3)分母不变,分子相加减;
(4)整理分子成积的形式
(5)约分,化为最简分式或整式
方法总结
三、分式的混合运算
例7:计算
算乘方,除法变乘法.
约分,做乘法.
同分母分式相减.
解:原式=
计算
解:原式=
通分,除法变乘法.
约分,去括号.
乘方,因式分解.
1. 观察运算类型.
2. 确定运算顺序:
①先乘方,再乘除,最后加减,有括号要先算括号里面的.
②识别出能因式分解的多项式,并知道何时需要因式分解.
3. 书写计算过程:书写清晰,不跳步.
温馨提示
四、分式的化简求值
例8 先化简 ,再求值: ,其中 .
解:原式=
当 时,原式
解:原式
解:原式
随堂练习
1.计算:
解:原式
解:原式
解:原式
解:
2.混合运算:
(2)
解:原式
解:原式
当a= +1时,原式= +1-1= .
3. 先化简,再求值 :(1- ) ÷ ,其中a= +1.
1.同分母的分式相加减,分母不变,分子相加减.
2.异分母的分式相加减,先通分,变为同分母的分式,然后再加减.
1.分式的分子和分母是多项式时,在进行运算时要适时添加括号
2.整式和分式之间进行加减运算时,则要把整式看成分母是1的分式,以便通分
3.异分母分式进行加减运算需要先通分,关键是确定最简公分母
分式的加减
注意
加减法运算
课堂小结
