16.4零指数幂与负整数指数幂 课件(共26张PPT)
文档属性
| 名称 | 16.4零指数幂与负整数指数幂 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
16.4 零指数幂与负整数指数幂
八年级下
华师版
1.理解零次幂及负整数指数幂的性质并应用其解决问题.
2.能灵活运用整数指数幂的运算性质进行相关计算.
3.能用科学记数法表示绝对值较小的数.
学习目标
重点
难点
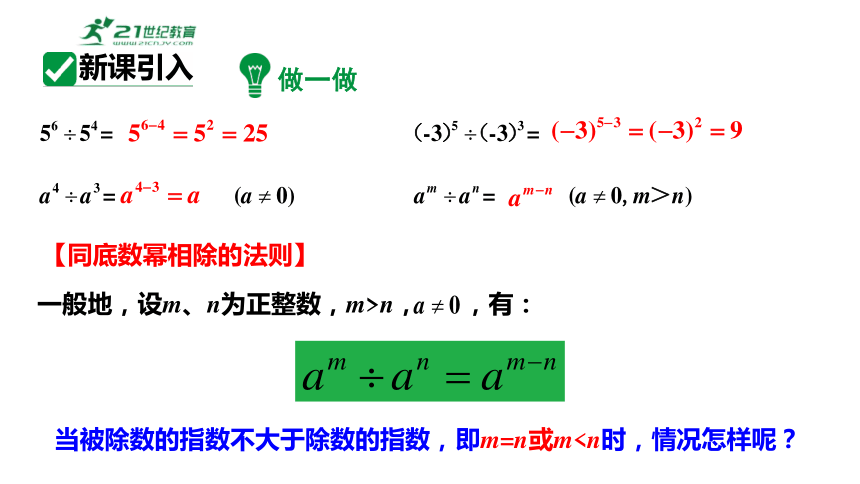
做一做
【同底数幂相除的法则】
当被除数的指数不大于除数的指数,即m=n或m一般地,设m、n为正整数,m>n, ,有:
新课引入
……
结论:
【同底数幂的除法法则】
【除法的意义】
……
1
1
1
一、零指数幂
新知学习
任何不等于零的数的零次幂都等于1.
理解
1.底数不为零,这是先决条件,不能忽略;00没有意义.
2.不管底数a是多么复杂的数或多项式,只要它不为零,那么a0的结果总是1.
( )
( )
×
√
√
√
√
例1 判断下列说法是否正确:
( )
( )
( )
例2 已知(2x-3)0=1,则x的取值范围是( )
A.x> B.x< C.x= D.x≠
D
根据零指数幂的意义,可得2x-3≠0,即x≠
方法总结:
零次幂有意义的条件是底数不等于0,所以解决有关零次幂的意义类型的题目时,可列出关于底数不等于0的式子求解即可.
例3 若(x-1)x+1=1,求x的值.
解:①当x+1=0,即x=-1时,原式=(-2)0=1;
②当x-1=1,x=2时,原式=13=1;
③当x-1=-1,x=0时,0+1=1不是偶数.故舍去.
故x=-1或2.
方法总结:
乘方的结果为1,可分为三种情况:不为零的数的零次幂等于1;1的任何次幂都等于1;-1的偶次幂等于1,即在底数不等于0的情况下考虑指数等于0;考虑底数等于1或-1.
……
结论:
【同底数幂的除法法则】
【除法的意义】
……
二、负整数指数幂
任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数
理解
1.负整指数幂成立的先决条件仍是底数不为零.
2.避免出现类似5-2=-25这样的错误.
例4 计算:
例5 用小数表示下列各数:
针对训练
计算:
解:
方法总结:
关键是理解负整数指数幂的意义,依次计算出结果.当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数(简称:底倒指反).
引入负整数指数和0指数后,正整数指数幂的其他几条运算性质能否推广到m、n是任意整数的情形
以am an=am+n这条性质为例:
(3)(a b)n= an bn (m,n是整数)
(1)am an=am+n(m,n是整数)
(2)(am)n=am n(m,n是整数)
(6)当a≠0,a0=1(a≠0)
三、整数指数幂运算性质
(5)
例6 计算:(1) (2)
复习回顾:
绝对值大于10的数记成a×10n的形式,其中1≤ |a| <10,n是正整数.
四、科学记数法
1. 864000可以写成 .
8.64×105
B
2.用科学记数法表示2130000,正确的是( )
A.21.3×105
B.2.13×106
C.0.213×107
D.213×104
怎样把0.0000864用科学记数法表示?
想一想
1.计算机的存储器完成一次存储的时间一般以百万分之一秒或十亿分之一秒为单位.
我们的周围还有很多很小的数
2.存在于生物体内的某种细胞的直径约为百万分之一米,即1微米.
3.人的头发丝的直径大约为0.000 07米,这个数已经很小了,但还有更小的如纳米,1纳米 = 十亿分之一米 .
指数与运算结果中0的个数有什么关系?你发现了什么规律
10的-n次幂,在1前面有______个0.
计算:
0.1
0.01
0.001
0.0001
0.00001
n
例如:
0.00001=_______; 0.0000001=_______.
观察
所以, 0.0000864=8.64 ×0.00001=8.64 ×10-5.
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成a×10- n的形式,其中n是正整数,1≤ |a| <10.
绝对值较大的数表示成a×10n的形式
绝对值较小的数表示成a×10- n的形式
科学记数法
例7 用科学记数法表示下列各数:
(1)0.00528 (2)-6341700
(3)-0.000002967 (4)22255300000
解:
(1)0.00528=5.28×10-3
(2)-6341700=-6.3417×106
(4)22255300000=2.22553×1010
(3)-0.000002967=-2.967×10-6
温馨提示
1.n等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面这个零).
2.用科学计数法表示一个负数时,不要忘了前面带“-”号.
3.表示一个有单位的数时,结果也要带单位.
随堂练习
1.若 则a、b、c、d从小到大依次排列的是( )
A.aB.dC.bD.cC
2.若 ,试求 的值.
解:1 mm =10-3 m,1 nm =10-9 m.
答:1 nm3 的空间可以放1018个1 nm3 的物体.
3. 纳米(nm)是非常小的长度单位,1 nm =10-9 m.把1 nm3 的物体放到乒乓球上,就如同把乒乓球放到地球上.1 mm3 的空间可以放多少个1 nm3 的物体(物体之间的间隙忽略不计)?
任何不等于零的数的零次幂都等于1.
即:当a≠0时,a0=1.
绝对值小于1的数可以用科学记数法表示成a×10-n的形式,其中n是正整数,1≤ |a| <10.
零指数幂与
负整数指数幂
科学计数法
负整数指数幂
零指数幂
任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数.
即:
课堂小结
16.4 零指数幂与负整数指数幂
八年级下
华师版
1.理解零次幂及负整数指数幂的性质并应用其解决问题.
2.能灵活运用整数指数幂的运算性质进行相关计算.
3.能用科学记数法表示绝对值较小的数.
学习目标
重点
难点
做一做
【同底数幂相除的法则】
当被除数的指数不大于除数的指数,即m=n或m
新课引入
……
结论:
【同底数幂的除法法则】
【除法的意义】
……
1
1
1
一、零指数幂
新知学习
任何不等于零的数的零次幂都等于1.
理解
1.底数不为零,这是先决条件,不能忽略;00没有意义.
2.不管底数a是多么复杂的数或多项式,只要它不为零,那么a0的结果总是1.
( )
( )
×
√
√
√
√
例1 判断下列说法是否正确:
( )
( )
( )
例2 已知(2x-3)0=1,则x的取值范围是( )
A.x> B.x< C.x= D.x≠
D
根据零指数幂的意义,可得2x-3≠0,即x≠
方法总结:
零次幂有意义的条件是底数不等于0,所以解决有关零次幂的意义类型的题目时,可列出关于底数不等于0的式子求解即可.
例3 若(x-1)x+1=1,求x的值.
解:①当x+1=0,即x=-1时,原式=(-2)0=1;
②当x-1=1,x=2时,原式=13=1;
③当x-1=-1,x=0时,0+1=1不是偶数.故舍去.
故x=-1或2.
方法总结:
乘方的结果为1,可分为三种情况:不为零的数的零次幂等于1;1的任何次幂都等于1;-1的偶次幂等于1,即在底数不等于0的情况下考虑指数等于0;考虑底数等于1或-1.
……
结论:
【同底数幂的除法法则】
【除法的意义】
……
二、负整数指数幂
任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数
理解
1.负整指数幂成立的先决条件仍是底数不为零.
2.避免出现类似5-2=-25这样的错误.
例4 计算:
例5 用小数表示下列各数:
针对训练
计算:
解:
方法总结:
关键是理解负整数指数幂的意义,依次计算出结果.当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数(简称:底倒指反).
引入负整数指数和0指数后,正整数指数幂的其他几条运算性质能否推广到m、n是任意整数的情形
以am an=am+n这条性质为例:
(3)(a b)n= an bn (m,n是整数)
(1)am an=am+n(m,n是整数)
(2)(am)n=am n(m,n是整数)
(6)当a≠0,a0=1(a≠0)
三、整数指数幂运算性质
(5)
例6 计算:(1) (2)
复习回顾:
绝对值大于10的数记成a×10n的形式,其中1≤ |a| <10,n是正整数.
四、科学记数法
1. 864000可以写成 .
8.64×105
B
2.用科学记数法表示2130000,正确的是( )
A.21.3×105
B.2.13×106
C.0.213×107
D.213×104
怎样把0.0000864用科学记数法表示?
想一想
1.计算机的存储器完成一次存储的时间一般以百万分之一秒或十亿分之一秒为单位.
我们的周围还有很多很小的数
2.存在于生物体内的某种细胞的直径约为百万分之一米,即1微米.
3.人的头发丝的直径大约为0.000 07米,这个数已经很小了,但还有更小的如纳米,1纳米 = 十亿分之一米 .
指数与运算结果中0的个数有什么关系?你发现了什么规律
10的-n次幂,在1前面有______个0.
计算:
0.1
0.01
0.001
0.0001
0.00001
n
例如:
0.00001=_______; 0.0000001=_______.
观察
所以, 0.0000864=8.64 ×0.00001=8.64 ×10-5.
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成a×10- n的形式,其中n是正整数,1≤ |a| <10.
绝对值较大的数表示成a×10n的形式
绝对值较小的数表示成a×10- n的形式
科学记数法
例7 用科学记数法表示下列各数:
(1)0.00528 (2)-6341700
(3)-0.000002967 (4)22255300000
解:
(1)0.00528=5.28×10-3
(2)-6341700=-6.3417×106
(4)22255300000=2.22553×1010
(3)-0.000002967=-2.967×10-6
温馨提示
1.n等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面这个零).
2.用科学计数法表示一个负数时,不要忘了前面带“-”号.
3.表示一个有单位的数时,结果也要带单位.
随堂练习
1.若 则a、b、c、d从小到大依次排列的是( )
A.a
2.若 ,试求 的值.
解:1 mm =10-3 m,1 nm =10-9 m.
答:1 nm3 的空间可以放1018个1 nm3 的物体.
3. 纳米(nm)是非常小的长度单位,1 nm =10-9 m.把1 nm3 的物体放到乒乓球上,就如同把乒乓球放到地球上.1 mm3 的空间可以放多少个1 nm3 的物体(物体之间的间隙忽略不计)?
任何不等于零的数的零次幂都等于1.
即:当a≠0时,a0=1.
绝对值小于1的数可以用科学记数法表示成a×10-n的形式,其中n是正整数,1≤ |a| <10.
零指数幂与
负整数指数幂
科学计数法
负整数指数幂
零指数幂
任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数.
即:
课堂小结
