17.2.2函数的图象 课件(共23张PPT)
文档属性
| 名称 | 17.2.2函数的图象 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
17.2.2 函数的图象
八年级下
华师版
1.了解函数图象的意义,掌握用描点法画函数图象的一般步骤.
2. 通过学习用图象法描述函数的过程,体验数形结合思想在研究问题中的重要作用.
3.能够准确的从图象中获取信息.
学习目标
重点
难点
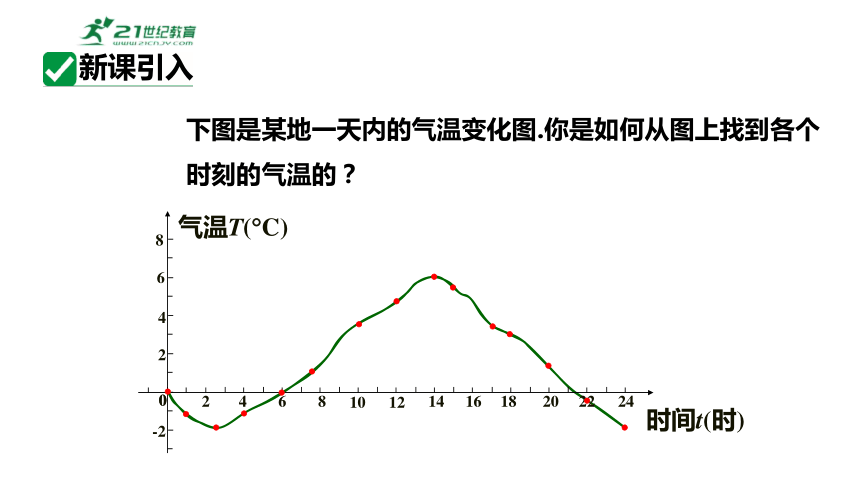
下图是某地一天内的气温变化图.你是如何从图上找到各个时刻的气温的?
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
新课引入
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
(10,3.5)
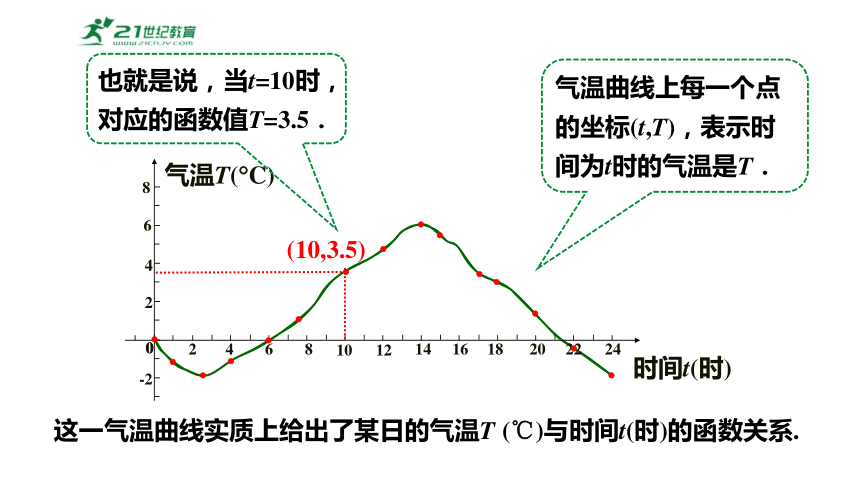
这一气温曲线实质上给出了某日的气温T (℃)与时间t(时)的函数关系.
也就是说,当t=10时,对应的函数值T=3.5.
气温曲线上每一个点的坐标(t,T),表示时间为t时的气温是T.
如,函数y=2x-3中,当自变量x=2时,函数y= .
则该函数的图象上一个点的坐标是( , ).
1
一般来说,函数的图象是由平面直角坐标系中的一系列点组成的图形.图象上每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示该自变量对应的函数值.
1
2
一、函数的图象
新知学习
例1 已知函数y=2x-1.
(1)试判断点A(-1,3)和点B 是否在此函数的图象上;
导引:(1)将点A,B的坐标分别代入y=2x-1,看点的坐标能否满足这个关系式即可.
解:(1)因为当x=-1时,y=2×(-1)-1=-3≠3,
所以点A不在函数y=2x-1的图象上.
因为当x= 时,y=2× -1=- ,
所以点B在函数y=2x-1的图象上.
方法总结
判断点P(x,y)是否在函数图象上的方法:
将x,y的值代入函数关系式,若能满足函数关系式,则这个点在函数的图象上;若不满足函数关系式,则这个点不在函数的图象上.
例1 已知函数y=2x-1.
(2)已知点C(a,a+1)在此函数的图象上,求a的值.
导引:(2)将点C(a,a+1)的坐标代入y=2x-1,可得到一个关于a的一元一次方程,求出a的值即可.
解:(2)因为点C(a,a+1)在函数y=2x-1的图象上,
所以把x=a,y=a+1代入y=2x-1,
得a+1=2a-1.
解得a=2.
方法总结
坐标含字母的点在函数图象上,求字母值的方法:
将坐标代入函数关系式中,得到一个关于该字母的方程,解这个方程即得字母的值.
二、用描点法画函数的图象
1、画出函数y=x+1的图象.
解:取自变量x的一些值,例如x=-3,-2,-1,0,1,2,3,…,计算出对应的函数值.
为表达方便,可列表如下:
x … -3 -2 -1 0 1 2 3 …
y … …
-2
-1
0
1
2
3
4
由这一系列的对应值,可以得到一系列的有序实数对:
…,(-3,-2),(-2,-1),(-1,0),
(0,1),(1,2),(2,3),(3,4),…
在平面直角坐标系中,描出这些有序实数对(坐标)的对应点,如图所示.
-3 -2 -1 O 1 2 3
4
3
2
1
-1
-2
x
y
(-3,-2)
(-2,-1)
(-1,0)
(0,1)
(1,2)
(2,3)
(3,4)
用光滑曲线依次把这些点连起来,便可得到该函数的图象,如图所示.
画函数图象的方法:
可以概括为列表、描点、连线三步,通常称为描点法.
-3 -2 -1 O 1 2 3
4
3
2
1
-1
-2
x
y
解:(1)列表:
x … -3 -2 -1 0 1 2 3 …
y … …
4.5
例2 画出函数y= 的图象.
2
0.5
0
0.5
2
4.5
-3 -2 -1 O 1 2 3
4
3
2
1
-1
-2
x
y
(2)描点
(3)连线:用光滑曲线连接.
三、从函数图象中获取信息
1、王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上山,然后追赶爷爷,两人都爬上了山顶.下图中的两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)之间的函数关系(从小强开始爬山时计时).
(1)小强让爷爷先上山多少米?
(2)山顶离山脚的距离有多少米?谁先爬上山顶?
(3)小强何时赶上爷爷?这时距山脚的距离是多
少?
分析:
这两条线段不是两人爬山行走的路线图,而是表示爬山时离开山脚的距离与所用时间的函数的图象.图象上每一个点的纵坐标表示到山脚的距离,横坐标表示爬山所用时间.
(1)小强让爷爷先上山多少米?
第(1)问意思为x=0时,两人分别距离山脚多远,即求小强出发时对应点的纵坐标.
解:(1)当x=0时,y小强=0,y爷爷=60,
∴小强让爷爷先上山60米.
(2)山顶离山脚的距离有多少米?谁先爬上山顶?
(3)小强何时赶上爷爷?这时距山脚的距离是多少?
(2)两图象的最高点坐标分别是 和 ,
∴山顶离山脚的距离有300米,小强先爬上山顶.
(3)∵两条线段交点坐标是(8,240),
∴小强经过8分钟赶上爷爷,
这时距山脚240米.
1.解决实际问题的关键是要看x轴与y轴所表示的实际量是什么,由此来判断图象上每一点的横纵坐标代表什么.
2.自变量的取值范围;
3.图象中函数随着自变量变化的规律.
温馨提示
1.下列图象不能表示y是x的函数的是( )
C
随堂练习
解:(1)列表:
2. 画出函数y= 的图象.
(2)描点
(3)连线:用光滑曲线连接.
x … -6 -3 -2 -1 … 1 2 3 6 …
y … … …
-1
-2
-3
-6
6
3
2
1
x
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6
y
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
为什么不取“0”?
3.如图所示是记录某人在24 h内的体温变化情况的图象.
(1)图中有哪两个变化的量?哪个变量是自变量?哪个变量是因变量?
图中有时间和体温这两个变化的量,时间是自变量,体温是因变量.
在这天中此人的最高体温约是36.7℃,最低体温约是35.9℃,最高体温是在18时达到的,最低体温是在4时达到的.
(2)这天中此人的最高、最低体温各是多少?分别是在什么时刻达到的?
(3) 21:00时此人的体温是多少?
(4) 这天体温达到36.2 ℃时是在什么时刻?
21:00时此人的体温是36.5℃.
6时和约23:15时.
(5)此人体温在哪几段时间上升?在哪几段时间下降?在哪几段时间变化最小?
在1~2,9~10,15~16时这3个时间段变化最小.
在1~2,4~7,8~9,10~11,12~14,15~16,17~18时这7个时间段上升;
在2~4,7~8,9~10,11~12,14~15,16~17,18~24时这7个时间段下降;
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.
1.弄清横、纵坐标表示的意义,
2.自变量的取值范围;
3.图象中函数随着自变量变化的规律.
函数的图像
用图象法表
示函数关系
从函数图象
中获取信息
课堂小结
17.2.2 函数的图象
八年级下
华师版
1.了解函数图象的意义,掌握用描点法画函数图象的一般步骤.
2. 通过学习用图象法描述函数的过程,体验数形结合思想在研究问题中的重要作用.
3.能够准确的从图象中获取信息.
学习目标
重点
难点
下图是某地一天内的气温变化图.你是如何从图上找到各个时刻的气温的?
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
新课引入
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
(10,3.5)
这一气温曲线实质上给出了某日的气温T (℃)与时间t(时)的函数关系.
也就是说,当t=10时,对应的函数值T=3.5.
气温曲线上每一个点的坐标(t,T),表示时间为t时的气温是T.
如,函数y=2x-3中,当自变量x=2时,函数y= .
则该函数的图象上一个点的坐标是( , ).
1
一般来说,函数的图象是由平面直角坐标系中的一系列点组成的图形.图象上每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示该自变量对应的函数值.
1
2
一、函数的图象
新知学习
例1 已知函数y=2x-1.
(1)试判断点A(-1,3)和点B 是否在此函数的图象上;
导引:(1)将点A,B的坐标分别代入y=2x-1,看点的坐标能否满足这个关系式即可.
解:(1)因为当x=-1时,y=2×(-1)-1=-3≠3,
所以点A不在函数y=2x-1的图象上.
因为当x= 时,y=2× -1=- ,
所以点B在函数y=2x-1的图象上.
方法总结
判断点P(x,y)是否在函数图象上的方法:
将x,y的值代入函数关系式,若能满足函数关系式,则这个点在函数的图象上;若不满足函数关系式,则这个点不在函数的图象上.
例1 已知函数y=2x-1.
(2)已知点C(a,a+1)在此函数的图象上,求a的值.
导引:(2)将点C(a,a+1)的坐标代入y=2x-1,可得到一个关于a的一元一次方程,求出a的值即可.
解:(2)因为点C(a,a+1)在函数y=2x-1的图象上,
所以把x=a,y=a+1代入y=2x-1,
得a+1=2a-1.
解得a=2.
方法总结
坐标含字母的点在函数图象上,求字母值的方法:
将坐标代入函数关系式中,得到一个关于该字母的方程,解这个方程即得字母的值.
二、用描点法画函数的图象
1、画出函数y=x+1的图象.
解:取自变量x的一些值,例如x=-3,-2,-1,0,1,2,3,…,计算出对应的函数值.
为表达方便,可列表如下:
x … -3 -2 -1 0 1 2 3 …
y … …
-2
-1
0
1
2
3
4
由这一系列的对应值,可以得到一系列的有序实数对:
…,(-3,-2),(-2,-1),(-1,0),
(0,1),(1,2),(2,3),(3,4),…
在平面直角坐标系中,描出这些有序实数对(坐标)的对应点,如图所示.
-3 -2 -1 O 1 2 3
4
3
2
1
-1
-2
x
y
(-3,-2)
(-2,-1)
(-1,0)
(0,1)
(1,2)
(2,3)
(3,4)
用光滑曲线依次把这些点连起来,便可得到该函数的图象,如图所示.
画函数图象的方法:
可以概括为列表、描点、连线三步,通常称为描点法.
-3 -2 -1 O 1 2 3
4
3
2
1
-1
-2
x
y
解:(1)列表:
x … -3 -2 -1 0 1 2 3 …
y … …
4.5
例2 画出函数y= 的图象.
2
0.5
0
0.5
2
4.5
-3 -2 -1 O 1 2 3
4
3
2
1
-1
-2
x
y
(2)描点
(3)连线:用光滑曲线连接.
三、从函数图象中获取信息
1、王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上山,然后追赶爷爷,两人都爬上了山顶.下图中的两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)之间的函数关系(从小强开始爬山时计时).
(1)小强让爷爷先上山多少米?
(2)山顶离山脚的距离有多少米?谁先爬上山顶?
(3)小强何时赶上爷爷?这时距山脚的距离是多
少?
分析:
这两条线段不是两人爬山行走的路线图,而是表示爬山时离开山脚的距离与所用时间的函数的图象.图象上每一个点的纵坐标表示到山脚的距离,横坐标表示爬山所用时间.
(1)小强让爷爷先上山多少米?
第(1)问意思为x=0时,两人分别距离山脚多远,即求小强出发时对应点的纵坐标.
解:(1)当x=0时,y小强=0,y爷爷=60,
∴小强让爷爷先上山60米.
(2)山顶离山脚的距离有多少米?谁先爬上山顶?
(3)小强何时赶上爷爷?这时距山脚的距离是多少?
(2)两图象的最高点坐标分别是 和 ,
∴山顶离山脚的距离有300米,小强先爬上山顶.
(3)∵两条线段交点坐标是(8,240),
∴小强经过8分钟赶上爷爷,
这时距山脚240米.
1.解决实际问题的关键是要看x轴与y轴所表示的实际量是什么,由此来判断图象上每一点的横纵坐标代表什么.
2.自变量的取值范围;
3.图象中函数随着自变量变化的规律.
温馨提示
1.下列图象不能表示y是x的函数的是( )
C
随堂练习
解:(1)列表:
2. 画出函数y= 的图象.
(2)描点
(3)连线:用光滑曲线连接.
x … -6 -3 -2 -1 … 1 2 3 6 …
y … … …
-1
-2
-3
-6
6
3
2
1
x
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6
y
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
为什么不取“0”?
3.如图所示是记录某人在24 h内的体温变化情况的图象.
(1)图中有哪两个变化的量?哪个变量是自变量?哪个变量是因变量?
图中有时间和体温这两个变化的量,时间是自变量,体温是因变量.
在这天中此人的最高体温约是36.7℃,最低体温约是35.9℃,最高体温是在18时达到的,最低体温是在4时达到的.
(2)这天中此人的最高、最低体温各是多少?分别是在什么时刻达到的?
(3) 21:00时此人的体温是多少?
(4) 这天体温达到36.2 ℃时是在什么时刻?
21:00时此人的体温是36.5℃.
6时和约23:15时.
(5)此人体温在哪几段时间上升?在哪几段时间下降?在哪几段时间变化最小?
在1~2,9~10,15~16时这3个时间段变化最小.
在1~2,4~7,8~9,10~11,12~14,15~16,17~18时这7个时间段上升;
在2~4,7~8,9~10,11~12,14~15,16~17,18~24时这7个时间段下降;
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.
1.弄清横、纵坐标表示的意义,
2.自变量的取值范围;
3.图象中函数随着自变量变化的规律.
函数的图像
用图象法表
示函数关系
从函数图象
中获取信息
课堂小结
