17.3.1一次函数 课件(共19张PPT)
文档属性
| 名称 | 17.3.1一次函数 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 17:03:05 | ||
图片预览






文档简介
(共19张PPT)
17.3.1 一次函数
八年级下
华师版
1.理解一次函数和正比例函数的概念,明确一次函数与正比例函数之间的联系.
2.能利用一次函数解决简单的实际问题.
学习目标
重点
难点
新课引入
问题1:小明暑假第一次去北京,汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时,已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系.
分析:汽车距北京的路程随着行车时间的变化而变化要想找出这两个变化着的量之间的关系,并据此得出相应的值.
解:设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米.
●A
行驶了95t千米
距北京s千米
全程570千米
则s与t之间的函数关系式为
s=570-95t.
北京★
问题2:文文准备将平时的零用钱节约些储存起来.他已存有50元,从现在起每个月节存12元.试写出文文的存款与从现在开始的月份之间的函数关系式.
解:设从现在开始的月份为x月,文文的存款为y元.
则y与x之间的函数关系式为
y=50+12x.
说明:
找出问题中的变量并用字母表示是探求函数关系的第一步,这里的y、x是两个变量,y是x的函数, x是自变量,y是因变量.
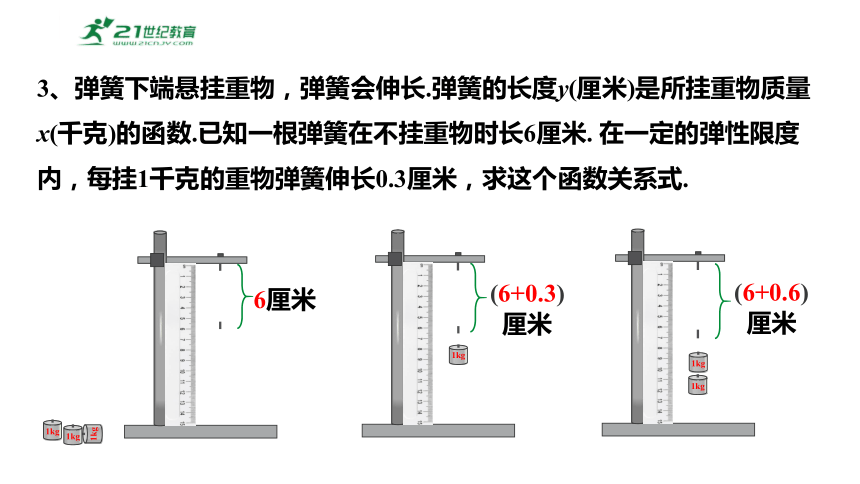
3、弹簧下端悬挂重物,弹簧会伸长.弹簧的长度y(厘米)是所挂重物质量x(千克)的函数.已知一根弹簧在不挂重物时长6厘米. 在一定的弹性限度内,每挂1千克的重物弹簧伸长0.3厘米,求这个函数关系式.
6厘米
(6+0.3)厘米
1kg
1kg
1kg
1kg
1kg
(6+0.6)厘米
1kg
解:∵每挂1千克重物弹簧伸长0.3厘米,
∴挂x千克重物时弹簧伸长0.3x厘米.
又∵不挂重物时弹簧的长度为6厘米,
∴挂x千克重物时弹簧长度为(0.3x+6)厘米.
即有 y=0.3x+6.
(x的取值范围由弹簧的弹性限度确定)
s=570-95t
y=50+12x
y=0.3x+6
上述函数的关系式都是用自变量的一次整式表示的,我们称它们为一次函数.
一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
特别地,当b=0时,一次函数y=kx(常数k≠0)也叫正比例函数.
s=-95t+570
y=12x+50
以上问题中的这几个函数有什么共同点
思考
新知学习
例1 下列函数关系中,哪些属于一次函数,其中哪些又属于正比例函数?
(1)面积为10cm2的三角形的底a(cm)与这边上的高h(cm);
(2)长为8(cm)的平行四边形的周长L(cm)与宽b(cm);
(3)食堂原有煤120吨,每天要用去5吨,x天后还剩下煤y吨;
(4)汽车每小时行40千米,行驶的路程s(千米)和时间t(小时).
说明:确定函数是否为一次函数或正比例函数,就是看它们的解析式经过整理后是否符合y=kx+b(k≠0)或y=kx(k≠0)的形式,所以此题必须先写出函数解析式后解答.
(1)面积为10cm2的三角形的底a(cm)与这边上的高h(cm);
(2)长为8(cm)的平行四边形的周长L(cm)与宽b(cm);
(3)食堂原有煤120吨,每天要用去5吨,x天后还剩下煤y吨;
(4)汽车每小时行40千米,行驶的路程s(千米)和时间t(小时).
不是一次函数;
(2) L=2b+16,
L是b的一次函数;
(3) y=120-5x,
y是x的一次函数;
(4) s=40t,
s是t的一次函数,也是正比例函数.
解:(1)
,
方法总结
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数项为零.
正比例函数是一次函数,但一次函数不一定是正比例函数.
例2 已知函数y=(k-2)x+2k+1,若它是一次函数,求k的值.若它是正比例函数,求k的值.
解:若y=(k-2)x+2k+1是一次函数,
则k-2≠0,即k≠2.
若y=(k-2)x+2k+1是正比例函数,
导引:根据一次函数和正比例函数的定义,求得k的值.
则2k+1=0,即k=
方法总结
函数是一次函数,则k≠0,且自变量的次数为1.
当b=0时,一次函数为正比例函数.
1、仓库内原有粉笔400盒. 如果每个星期领出36盒,求仓库内余下的粉笔盒数Q与星期数t之间的函数关系式.
解:Q=400-36t
(t取不超过11的正整数).
原有粉笔400盒
36盒
36盒
...
t星期共领36t盒
余下Q盒
随堂练习
2、已知 是关于 x 的一次函数,求 m 的值.
解:由题意得 m2 - 3 = 1,且 m - 2 ≠ 0,
解得 m = -2.
所以 m = -2.
分析:
一次函数
y = kx + b
x 的次数为 1
m2 - 3 = 1
m = 2 或 -2
k ≠ 0
m - 2 ≠ 0
m ≠ 2
3.为保护生态环境,防止水土流失,政府投资4万元给某村民小组,用于购买种植与移栽A,B两种树苗共1 000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知这两种树苗的单价及移栽费用见下表:
树苗品种 A树苗 B树苗
单价(元/棵) 20 32
移栽 费用 (元/棵) 3 5
设购买A树苗x棵,将这些树苗种植完成后,村民小组获得的纯收入为y元.求y与x之间的函数关系式.
解:由题意得,y=40000-(20+3)x-(32+5)(1000-x)=14x+3000,
则y与x之间的函数关系式为y=14x+3000.
4、某地区电话的月租费为 25 元,在此基础上,可免费打 50 次电话 (每次 3 分钟),超过 50 次后,每次 0.2 元.
(1) 写出每月电话费 y (元) 与通话次数 x (x > 50) 的函数关系式;
(2) 求出月通话 150 次的电话费;
解:(1) 根据题意得,y = 25 + (x - 50)×0.2,即 y = 0.2x + 15;
(2) 当 x = 150 时,y = 0.2 × 150 + 15 = 45
答:月通话 150 次的电话费是 45 元.
4、某地区电话的月租费为 25 元,在此基础上,可免费打 50 次电话 (每次 3 分钟),超过 50 次后,每次 0.2 元.
(3) 如果某月通话费为 53.6 元,求该月通话的次数.
解:(3) 因为 53.6 > 25,可知通话次数大于 50 次,
即当 y = 53.6 时,53.6 = 0.2x + 15,
解得 x = 193.
答:该月通话的次数为 193.
一般地,形如y=kx+b(k,b为常数,且k≠0)的函数叫做一次函数,其中x是自变量,y是x的函数.
特别地,当b=0时,y=kx(k为常数,k≠0),y叫做x的正比例函数.
说明:
(1)正比例函数是特殊的一次函数,一次函数包括正比例函数;
(2)判断一个函数是否是一次函数,必须将其化成最简形式,看是否是自变量的一次多项式的形式.
一次函数和正比例函数
课堂小结
17.3.1 一次函数
八年级下
华师版
1.理解一次函数和正比例函数的概念,明确一次函数与正比例函数之间的联系.
2.能利用一次函数解决简单的实际问题.
学习目标
重点
难点
新课引入
问题1:小明暑假第一次去北京,汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时,已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系.
分析:汽车距北京的路程随着行车时间的变化而变化要想找出这两个变化着的量之间的关系,并据此得出相应的值.
解:设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米.
●A
行驶了95t千米
距北京s千米
全程570千米
则s与t之间的函数关系式为
s=570-95t.
北京★
问题2:文文准备将平时的零用钱节约些储存起来.他已存有50元,从现在起每个月节存12元.试写出文文的存款与从现在开始的月份之间的函数关系式.
解:设从现在开始的月份为x月,文文的存款为y元.
则y与x之间的函数关系式为
y=50+12x.
说明:
找出问题中的变量并用字母表示是探求函数关系的第一步,这里的y、x是两个变量,y是x的函数, x是自变量,y是因变量.
3、弹簧下端悬挂重物,弹簧会伸长.弹簧的长度y(厘米)是所挂重物质量x(千克)的函数.已知一根弹簧在不挂重物时长6厘米. 在一定的弹性限度内,每挂1千克的重物弹簧伸长0.3厘米,求这个函数关系式.
6厘米
(6+0.3)厘米
1kg
1kg
1kg
1kg
1kg
(6+0.6)厘米
1kg
解:∵每挂1千克重物弹簧伸长0.3厘米,
∴挂x千克重物时弹簧伸长0.3x厘米.
又∵不挂重物时弹簧的长度为6厘米,
∴挂x千克重物时弹簧长度为(0.3x+6)厘米.
即有 y=0.3x+6.
(x的取值范围由弹簧的弹性限度确定)
s=570-95t
y=50+12x
y=0.3x+6
上述函数的关系式都是用自变量的一次整式表示的,我们称它们为一次函数.
一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
特别地,当b=0时,一次函数y=kx(常数k≠0)也叫正比例函数.
s=-95t+570
y=12x+50
以上问题中的这几个函数有什么共同点
思考
新知学习
例1 下列函数关系中,哪些属于一次函数,其中哪些又属于正比例函数?
(1)面积为10cm2的三角形的底a(cm)与这边上的高h(cm);
(2)长为8(cm)的平行四边形的周长L(cm)与宽b(cm);
(3)食堂原有煤120吨,每天要用去5吨,x天后还剩下煤y吨;
(4)汽车每小时行40千米,行驶的路程s(千米)和时间t(小时).
说明:确定函数是否为一次函数或正比例函数,就是看它们的解析式经过整理后是否符合y=kx+b(k≠0)或y=kx(k≠0)的形式,所以此题必须先写出函数解析式后解答.
(1)面积为10cm2的三角形的底a(cm)与这边上的高h(cm);
(2)长为8(cm)的平行四边形的周长L(cm)与宽b(cm);
(3)食堂原有煤120吨,每天要用去5吨,x天后还剩下煤y吨;
(4)汽车每小时行40千米,行驶的路程s(千米)和时间t(小时).
不是一次函数;
(2) L=2b+16,
L是b的一次函数;
(3) y=120-5x,
y是x的一次函数;
(4) s=40t,
s是t的一次函数,也是正比例函数.
解:(1)
,
方法总结
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数项为零.
正比例函数是一次函数,但一次函数不一定是正比例函数.
例2 已知函数y=(k-2)x+2k+1,若它是一次函数,求k的值.若它是正比例函数,求k的值.
解:若y=(k-2)x+2k+1是一次函数,
则k-2≠0,即k≠2.
若y=(k-2)x+2k+1是正比例函数,
导引:根据一次函数和正比例函数的定义,求得k的值.
则2k+1=0,即k=
方法总结
函数是一次函数,则k≠0,且自变量的次数为1.
当b=0时,一次函数为正比例函数.
1、仓库内原有粉笔400盒. 如果每个星期领出36盒,求仓库内余下的粉笔盒数Q与星期数t之间的函数关系式.
解:Q=400-36t
(t取不超过11的正整数).
原有粉笔400盒
36盒
36盒
...
t星期共领36t盒
余下Q盒
随堂练习
2、已知 是关于 x 的一次函数,求 m 的值.
解:由题意得 m2 - 3 = 1,且 m - 2 ≠ 0,
解得 m = -2.
所以 m = -2.
分析:
一次函数
y = kx + b
x 的次数为 1
m2 - 3 = 1
m = 2 或 -2
k ≠ 0
m - 2 ≠ 0
m ≠ 2
3.为保护生态环境,防止水土流失,政府投资4万元给某村民小组,用于购买种植与移栽A,B两种树苗共1 000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知这两种树苗的单价及移栽费用见下表:
树苗品种 A树苗 B树苗
单价(元/棵) 20 32
移栽 费用 (元/棵) 3 5
设购买A树苗x棵,将这些树苗种植完成后,村民小组获得的纯收入为y元.求y与x之间的函数关系式.
解:由题意得,y=40000-(20+3)x-(32+5)(1000-x)=14x+3000,
则y与x之间的函数关系式为y=14x+3000.
4、某地区电话的月租费为 25 元,在此基础上,可免费打 50 次电话 (每次 3 分钟),超过 50 次后,每次 0.2 元.
(1) 写出每月电话费 y (元) 与通话次数 x (x > 50) 的函数关系式;
(2) 求出月通话 150 次的电话费;
解:(1) 根据题意得,y = 25 + (x - 50)×0.2,即 y = 0.2x + 15;
(2) 当 x = 150 时,y = 0.2 × 150 + 15 = 45
答:月通话 150 次的电话费是 45 元.
4、某地区电话的月租费为 25 元,在此基础上,可免费打 50 次电话 (每次 3 分钟),超过 50 次后,每次 0.2 元.
(3) 如果某月通话费为 53.6 元,求该月通话的次数.
解:(3) 因为 53.6 > 25,可知通话次数大于 50 次,
即当 y = 53.6 时,53.6 = 0.2x + 15,
解得 x = 193.
答:该月通话的次数为 193.
一般地,形如y=kx+b(k,b为常数,且k≠0)的函数叫做一次函数,其中x是自变量,y是x的函数.
特别地,当b=0时,y=kx(k为常数,k≠0),y叫做x的正比例函数.
说明:
(1)正比例函数是特殊的一次函数,一次函数包括正比例函数;
(2)判断一个函数是否是一次函数,必须将其化成最简形式,看是否是自变量的一次多项式的形式.
一次函数和正比例函数
课堂小结
