20.3数据的离散程度 课件(共24张PPT)
文档属性
| 名称 | 20.3数据的离散程度 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 17:03:05 | ||
图片预览





文档简介
(共24张PPT)
20.3 数据的离散程度
八年级下
华师版
1.理解方差的概念及统计学意义.
2.会计算一组数据的方差.
3.能够运用方差判断数据的波动程度,并解决简单的实际问题.
学习目标
重点
难点
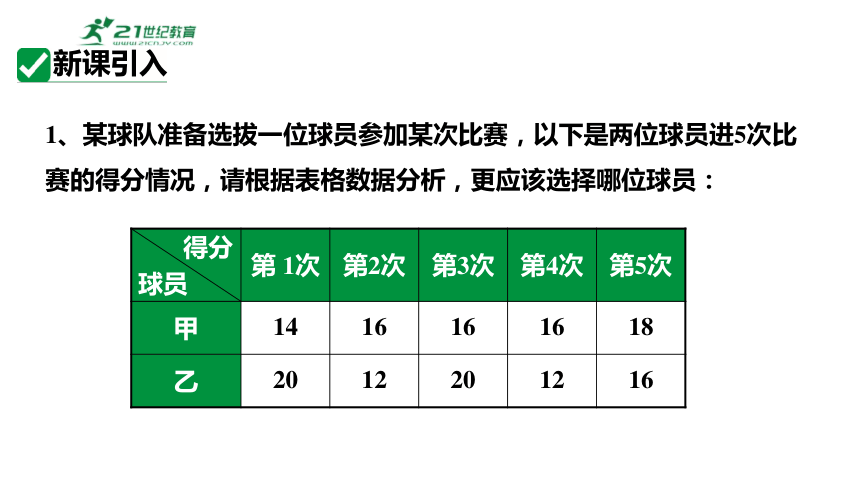
1、某球队准备选拔一位球员参加某次比赛,以下是两位球员进5次比赛的得分情况,请根据表格数据分析,更应该选择哪位球员:
得分 球员 第 1次 第2次 第3次 第4次 第5次
甲 14 16 16 16 18
乙 20 12 20 12 16
新课引入
根据我们已经学习过的平均数、中位数、众数,可以选拔出想要的球员吗?
思考
平均数 中位数 众数
甲 16 16 16
乙 16 16 20(12)
根据表格中的数据,甲、乙两位球员前5次比赛得分的平均数和中位数都相同,众数也无法比较.
此时,应当如何选择球员呢?
需要考虑稳定性的因素
问题1
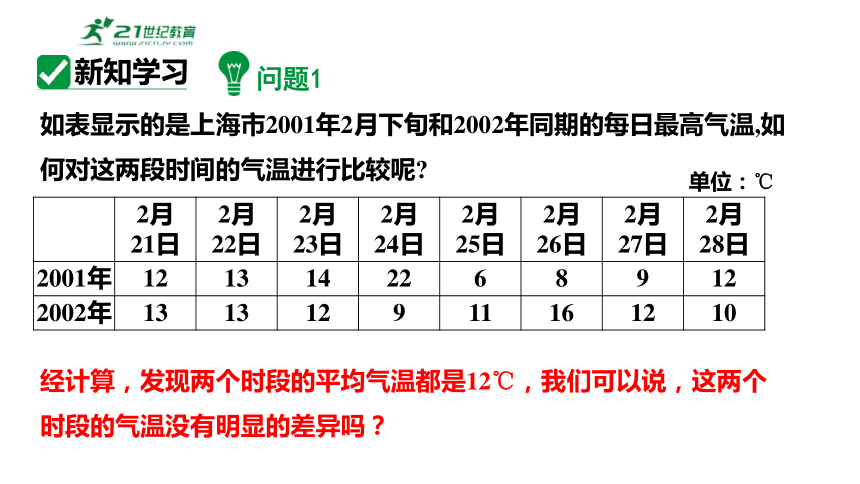
如表显示的是上海市2001年2月下旬和2002年同期的每日最高气温,如何对这两段时间的气温进行比较呢
2月 21日 2月 22日 2月 23日 2月 24日 2月 25日 2月 26日 2月 27日 2月
28日
2001年 12 13 14 22 6 8 9 12
2002年 13 13 12 9 11 16 12 10
单位:℃
经计算,发现两个时段的平均气温都是12℃,我们可以说,这两个时段的气温没有明显的差异吗?
新知学习
通过散点图可知:2001年气温的点波动范围比较大——从6℃到22℃,气温最大值与最小值之间差距很大,相差16℃;2002年气温的点波动范围比较小——从9℃到16℃,气温的最大值与最小值相差7℃,总体上气温变化的范围不太大.
2001年
2002年
思考
我们常说,一个城市“四季温差不大”,一个城市“四季分明”,这代表了什么含义呢
青岛“四季分明”
昆明“四季如春”
代表青岛一年温度波动很大.
代表昆明一年温度波动很小.
问题2
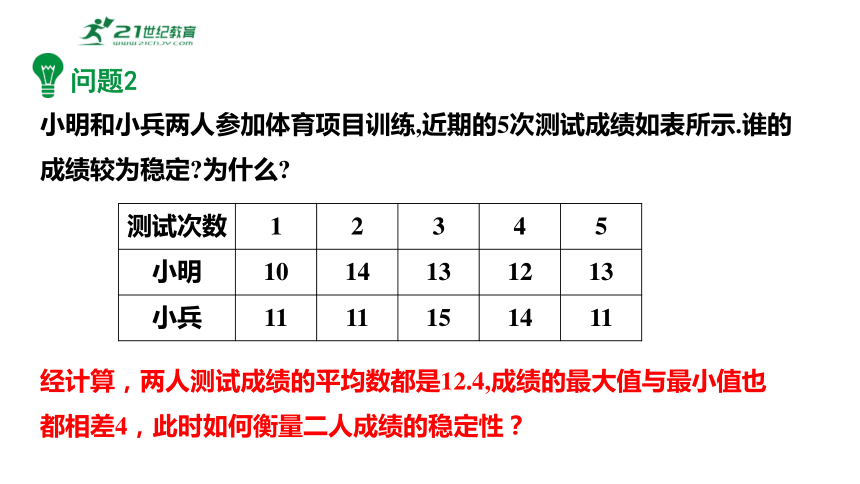
小明和小兵两人参加体育项目训练,近期的5次测试成绩如表所示.谁的成绩较为稳定 为什么
测试次数 1 2 3 4 5
小明 10 14 13 12 13
小兵 11 11 15 14 11
经计算,两人测试成绩的平均数都是12.4,成绩的最大值与最小值也都相差4,此时如何衡量二人成绩的稳定性?
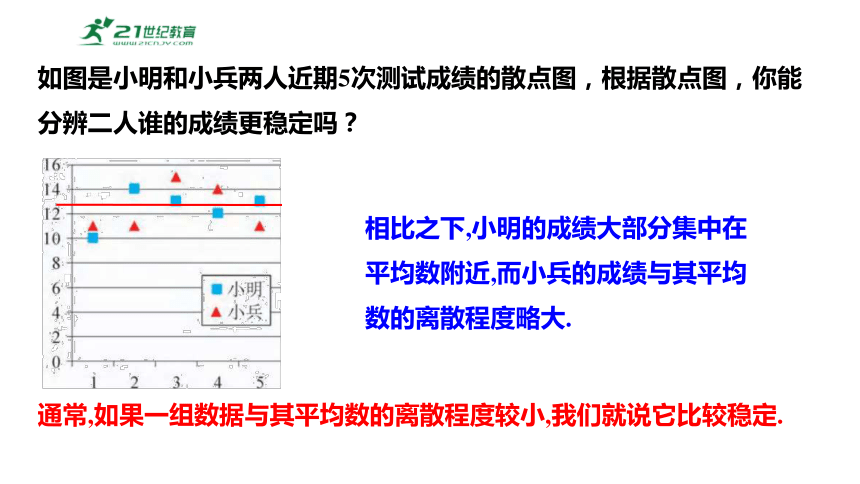
如图是小明和小兵两人近期5次测试成绩的散点图,根据散点图,你能分辨二人谁的成绩更稳定吗?
相比之下,小明的成绩大部分集中在平均数附近,而小兵的成绩与其平均数的离散程度略大.
通常,如果一组数据与其平均数的离散程度较小,我们就说它比较稳定.
思考
怎样的指标能反映一组数据与其平均数的离散程度呢?
1 2 3 4 5 求和
小明 每次测试成绩 10 14 13 12 13
每次成绩-平均成绩
小兵 每次测试成绩 11 11 15 14 11
每次成绩-平均成绩
如果把小明和小兵的成绩与平均成绩做差值进行累加比较可行吗?
-2.4 1.6 0.6 -0.4 0.6
-1.4 -1.4 2.6 1.6 -1.4
0
0
思考
如何改进该比较方法?
成绩与平均成绩的差值会有负数,可以采用平方的形式,使其化为正数.
1 2 3 4 5 求和
小明 每次测试成绩 10 14 13 12 13
(每次成绩-平均成绩)2
小兵 每次测试成绩 11 11 15 14 11
(每次成绩-平均成绩)2
从表中数据可以知道,小明的成绩更稳定.
1.96 1.96 6.76 2.56 1.96 15.2
5.76 2.56 0.36 0.16 0.36 9.2
思考
如果一共进行了7次测试,小明因故缺席了2次,怎样比较谁的成绩更稳定 请将你的方法与数据填入表中.
1 2 3 4 5 6 7 求和
小明 每次测试成绩 10 14 13 缺席 12 缺席 13
(每次成绩-平均成绩)2
小兵 每次测试成绩 11 11 15 11 14 14 11
(每次成绩-平均成绩)2
小明少2次成绩,如果直接给“(每次成绩-平均成绩)2”求和,不能体现二人成绩稳定性.
5.76 2.56 0.36 0.16 0.36 9.2
2.04 2.04 6.61 2.04 2.47 2.47 2.04 19.71
小明缺少两次成绩,如何与小兵进行合理的比较呢?
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果称为方差.
我们通常用x1,x2,…表示各个原始数据,用 表示一组数据的平均数.小明和小兵5次测试成绩的方差的计算式就是:
计算得:
小明5次测试成绩的方差为 ,
小兵5次测试成绩的方差为 .
1.84
3.04
小明5次测试成绩的方差小于小兵5次测试成绩的方差,则表明小明5次测试成绩更加稳定.
动手
请你计算测试7次,小明缺考两次时二人成绩的方差.
例1 比较下列两组数据的方差:
A组:0,10,5,5,5,5,5,5,5,5;
B组:4,6,3,7,2,8,1,9,5,5
解:A组数据的方差为:5;B组数据的方差为:6
A组数据的方差小于B组数据.
例2 算一算,第150页问题1中哪一年2月下旬每日最高气温的离散程度较大 与你从图20.3.1中直观看出的结果一致吗
2月 21日 2月 22日 2月 23日 2月 24日 2月 25日 2月 26日 2月 27日 2月
28日
2001年 12 13 14 22 6 8 9 12
2002年 13 13 12 9 11 16 12 10
解:计算得2001年2月下旬气温的方差为:20.75;2002年2月下旬气温的方差为:4
2001年2月下旬气温离散程度较大,与图20.3.1中直观看出的结果一致.
我们可以用计算器求平均数、中位数、众数,也可以用计算器求方差吗?
?
用计算器求方差
例:计算2002年2月下旬的上海市每日最高气温的方差.
用Excel求方差:
1.样本方差的作用是( )
A.表示总体的平均水平
B.表示样本的平均水平
C.准确表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
D
随堂练习
2. 人数相同的八年级 (1)、(2) 两班学生在同一次数学单元测试中,班级平均分和方差如下:
, , ,则成绩较为稳定的班级是( )
A. 甲班 B. 乙班
C. 两班成绩一样稳定 D. 无法确定
B
3.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行 10次测验,成绩 (单位:分) 如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1) 填写下表:
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84 84 0.3
乙 84 84 34
84
90
0.5
14.4
(2) 利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
解:从众数看,甲成绩的众数为 84 分,乙成绩的众数是 90 分,乙的成绩比甲好;
从方差看,s2甲 = 14.4, s2乙 = 34,甲的成绩比乙相对稳定;从甲、乙的中位数、平均数看,中位数、平均数都是84 分,两人成绩一样好;
数据的离散
程度
方差:“先平均,再求差,然后平方,最后再平均”得到的结果
方差越小,数据的波动程度就越小,数据就越稳定.
课堂小结
20.3 数据的离散程度
八年级下
华师版
1.理解方差的概念及统计学意义.
2.会计算一组数据的方差.
3.能够运用方差判断数据的波动程度,并解决简单的实际问题.
学习目标
重点
难点
1、某球队准备选拔一位球员参加某次比赛,以下是两位球员进5次比赛的得分情况,请根据表格数据分析,更应该选择哪位球员:
得分 球员 第 1次 第2次 第3次 第4次 第5次
甲 14 16 16 16 18
乙 20 12 20 12 16
新课引入
根据我们已经学习过的平均数、中位数、众数,可以选拔出想要的球员吗?
思考
平均数 中位数 众数
甲 16 16 16
乙 16 16 20(12)
根据表格中的数据,甲、乙两位球员前5次比赛得分的平均数和中位数都相同,众数也无法比较.
此时,应当如何选择球员呢?
需要考虑稳定性的因素
问题1
如表显示的是上海市2001年2月下旬和2002年同期的每日最高气温,如何对这两段时间的气温进行比较呢
2月 21日 2月 22日 2月 23日 2月 24日 2月 25日 2月 26日 2月 27日 2月
28日
2001年 12 13 14 22 6 8 9 12
2002年 13 13 12 9 11 16 12 10
单位:℃
经计算,发现两个时段的平均气温都是12℃,我们可以说,这两个时段的气温没有明显的差异吗?
新知学习
通过散点图可知:2001年气温的点波动范围比较大——从6℃到22℃,气温最大值与最小值之间差距很大,相差16℃;2002年气温的点波动范围比较小——从9℃到16℃,气温的最大值与最小值相差7℃,总体上气温变化的范围不太大.
2001年
2002年
思考
我们常说,一个城市“四季温差不大”,一个城市“四季分明”,这代表了什么含义呢
青岛“四季分明”
昆明“四季如春”
代表青岛一年温度波动很大.
代表昆明一年温度波动很小.
问题2
小明和小兵两人参加体育项目训练,近期的5次测试成绩如表所示.谁的成绩较为稳定 为什么
测试次数 1 2 3 4 5
小明 10 14 13 12 13
小兵 11 11 15 14 11
经计算,两人测试成绩的平均数都是12.4,成绩的最大值与最小值也都相差4,此时如何衡量二人成绩的稳定性?
如图是小明和小兵两人近期5次测试成绩的散点图,根据散点图,你能分辨二人谁的成绩更稳定吗?
相比之下,小明的成绩大部分集中在平均数附近,而小兵的成绩与其平均数的离散程度略大.
通常,如果一组数据与其平均数的离散程度较小,我们就说它比较稳定.
思考
怎样的指标能反映一组数据与其平均数的离散程度呢?
1 2 3 4 5 求和
小明 每次测试成绩 10 14 13 12 13
每次成绩-平均成绩
小兵 每次测试成绩 11 11 15 14 11
每次成绩-平均成绩
如果把小明和小兵的成绩与平均成绩做差值进行累加比较可行吗?
-2.4 1.6 0.6 -0.4 0.6
-1.4 -1.4 2.6 1.6 -1.4
0
0
思考
如何改进该比较方法?
成绩与平均成绩的差值会有负数,可以采用平方的形式,使其化为正数.
1 2 3 4 5 求和
小明 每次测试成绩 10 14 13 12 13
(每次成绩-平均成绩)2
小兵 每次测试成绩 11 11 15 14 11
(每次成绩-平均成绩)2
从表中数据可以知道,小明的成绩更稳定.
1.96 1.96 6.76 2.56 1.96 15.2
5.76 2.56 0.36 0.16 0.36 9.2
思考
如果一共进行了7次测试,小明因故缺席了2次,怎样比较谁的成绩更稳定 请将你的方法与数据填入表中.
1 2 3 4 5 6 7 求和
小明 每次测试成绩 10 14 13 缺席 12 缺席 13
(每次成绩-平均成绩)2
小兵 每次测试成绩 11 11 15 11 14 14 11
(每次成绩-平均成绩)2
小明少2次成绩,如果直接给“(每次成绩-平均成绩)2”求和,不能体现二人成绩稳定性.
5.76 2.56 0.36 0.16 0.36 9.2
2.04 2.04 6.61 2.04 2.47 2.47 2.04 19.71
小明缺少两次成绩,如何与小兵进行合理的比较呢?
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果称为方差.
我们通常用x1,x2,…表示各个原始数据,用 表示一组数据的平均数.小明和小兵5次测试成绩的方差的计算式就是:
计算得:
小明5次测试成绩的方差为 ,
小兵5次测试成绩的方差为 .
1.84
3.04
小明5次测试成绩的方差小于小兵5次测试成绩的方差,则表明小明5次测试成绩更加稳定.
动手
请你计算测试7次,小明缺考两次时二人成绩的方差.
例1 比较下列两组数据的方差:
A组:0,10,5,5,5,5,5,5,5,5;
B组:4,6,3,7,2,8,1,9,5,5
解:A组数据的方差为:5;B组数据的方差为:6
A组数据的方差小于B组数据.
例2 算一算,第150页问题1中哪一年2月下旬每日最高气温的离散程度较大 与你从图20.3.1中直观看出的结果一致吗
2月 21日 2月 22日 2月 23日 2月 24日 2月 25日 2月 26日 2月 27日 2月
28日
2001年 12 13 14 22 6 8 9 12
2002年 13 13 12 9 11 16 12 10
解:计算得2001年2月下旬气温的方差为:20.75;2002年2月下旬气温的方差为:4
2001年2月下旬气温离散程度较大,与图20.3.1中直观看出的结果一致.
我们可以用计算器求平均数、中位数、众数,也可以用计算器求方差吗?
?
用计算器求方差
例:计算2002年2月下旬的上海市每日最高气温的方差.
用Excel求方差:
1.样本方差的作用是( )
A.表示总体的平均水平
B.表示样本的平均水平
C.准确表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
D
随堂练习
2. 人数相同的八年级 (1)、(2) 两班学生在同一次数学单元测试中,班级平均分和方差如下:
, , ,则成绩较为稳定的班级是( )
A. 甲班 B. 乙班
C. 两班成绩一样稳定 D. 无法确定
B
3.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行 10次测验,成绩 (单位:分) 如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1) 填写下表:
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84 84 0.3
乙 84 84 34
84
90
0.5
14.4
(2) 利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
解:从众数看,甲成绩的众数为 84 分,乙成绩的众数是 90 分,乙的成绩比甲好;
从方差看,s2甲 = 14.4, s2乙 = 34,甲的成绩比乙相对稳定;从甲、乙的中位数、平均数看,中位数、平均数都是84 分,两人成绩一样好;
数据的离散
程度
方差:“先平均,再求差,然后平方,最后再平均”得到的结果
方差越小,数据的波动程度就越小,数据就越稳定.
课堂小结
