江苏省南京市重点中学2022年初升高特长生考试数学试卷1(含解析)
文档属性
| 名称 | 江苏省南京市重点中学2022年初升高特长生考试数学试卷1(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 766.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-13 00:00:00 | ||
图片预览


文档简介
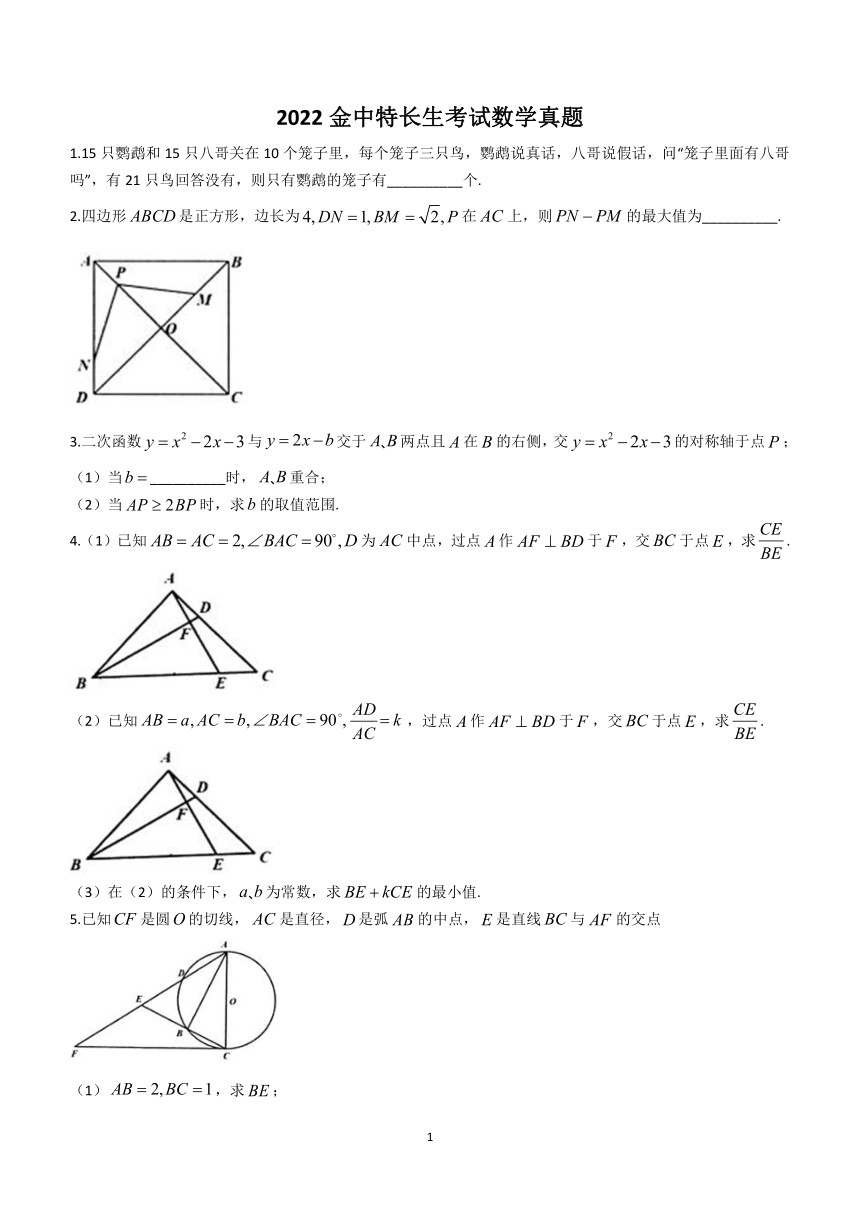
2022金中特长生考试数学真题
1.15只鹦鹉和15只八哥关在10个笼子里,每个笼子三只鸟,鹦鹉说真话,八哥说假话,问“笼子里面有八哥吗”,有21只鸟回答没有,则只有鹦鹉的笼子有__________个.
2.四边形是正方形,边长为在上,则的最大值为__________.
3.二次函数与交于两点且在的右侧,交的对称轴于点;
(1)当__________时,重合;
(2)当时,求的取值范围.
4.(1)已知为中点,过点作于,交于点,求.
(2)已知,过点作于,交于点,求.
(3)在(2)的条件下,为常数,求的最小值.
5.已知是圆的切线,是直径,是弧的中点,是直线与的交点
(1),求;
(2),求.
6.可以表示为数轴上1右边的点
(1)可以在平面直角坐标系中表示为__________;
(2)在坐标系中用阴影表示满足的点;
(3)与上述阴影部分围成的封闭图形中包含2个整点(横纵坐标均为整数的点)求的取值范围.
2022金中特长生考试数学真题解析
1.【解析】分三类情况:笼子里只有鹦鹉(①),笼子里只有八哥(②),笼子里既有鹦鹉也有八哥(③),①所有鹦鹉都说没有,②所有八哥都回答没有,③鹦鹉都回签有 八哥都回答没有,由此可得无论何种情况八哥都回答没有,所以回答没有的鹦鹉有6只,.
2.【解析】作点关于的对称点,连接此题对称点,一样可以解决.
3.【解析】(1)联立得:,消去得,
由得::
(2)设点的横坐标分别为,点的横坐标为1
则
由可知:,
且
解得:
4.【解析】法一:过点作平行,交的延长线于点
易证,
法二:过点作交于点,由平行线分线段成比例可知:
由射影定理可知:,
法三:由梅氏定理可知:
(2)【解析】第一问的三种方法依然活用,此外省略具体计算过程,给出结果
(3)【解析】法一:,
,
设,则
当,且此时,符合題意
的最小值为
法二:过点作的垂线,交于点,则,
,设,
取中点,过点作的垂线段,
,即,
,解得:,
的最小值是
5.【解析】连接,由为弧可知:平分,
是等腰三角形,,
(1);
(2)由射影定理可知:;
6.【解析】(1)直线上方区域(不含边界)
(2)如图所示,不包含边界部分:
(3)考虑两种临界情况:直线过或为临界位置,中间情况包含和两个整点,
1.15只鹦鹉和15只八哥关在10个笼子里,每个笼子三只鸟,鹦鹉说真话,八哥说假话,问“笼子里面有八哥吗”,有21只鸟回答没有,则只有鹦鹉的笼子有__________个.
2.四边形是正方形,边长为在上,则的最大值为__________.
3.二次函数与交于两点且在的右侧,交的对称轴于点;
(1)当__________时,重合;
(2)当时,求的取值范围.
4.(1)已知为中点,过点作于,交于点,求.
(2)已知,过点作于,交于点,求.
(3)在(2)的条件下,为常数,求的最小值.
5.已知是圆的切线,是直径,是弧的中点,是直线与的交点
(1),求;
(2),求.
6.可以表示为数轴上1右边的点
(1)可以在平面直角坐标系中表示为__________;
(2)在坐标系中用阴影表示满足的点;
(3)与上述阴影部分围成的封闭图形中包含2个整点(横纵坐标均为整数的点)求的取值范围.
2022金中特长生考试数学真题解析
1.【解析】分三类情况:笼子里只有鹦鹉(①),笼子里只有八哥(②),笼子里既有鹦鹉也有八哥(③),①所有鹦鹉都说没有,②所有八哥都回答没有,③鹦鹉都回签有 八哥都回答没有,由此可得无论何种情况八哥都回答没有,所以回答没有的鹦鹉有6只,.
2.【解析】作点关于的对称点,连接此题对称点,一样可以解决.
3.【解析】(1)联立得:,消去得,
由得::
(2)设点的横坐标分别为,点的横坐标为1
则
由可知:,
且
解得:
4.【解析】法一:过点作平行,交的延长线于点
易证,
法二:过点作交于点,由平行线分线段成比例可知:
由射影定理可知:,
法三:由梅氏定理可知:
(2)【解析】第一问的三种方法依然活用,此外省略具体计算过程,给出结果
(3)【解析】法一:,
,
设,则
当,且此时,符合題意
的最小值为
法二:过点作的垂线,交于点,则,
,设,
取中点,过点作的垂线段,
,即,
,解得:,
的最小值是
5.【解析】连接,由为弧可知:平分,
是等腰三角形,,
(1);
(2)由射影定理可知:;
6.【解析】(1)直线上方区域(不含边界)
(2)如图所示,不包含边界部分:
(3)考虑两种临界情况:直线过或为临界位置,中间情况包含和两个整点,
同课章节目录
