五年级下册数学北师大版第四课时 露在外面的面课件(共35张PPT)
文档属性
| 名称 | 五年级下册数学北师大版第四课时 露在外面的面课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-13 00:00:00 | ||
图片预览




文档简介
(共35张PPT)
1、一间教室长8m、宽6m、高3m。要给教室的墙壁和房顶粉刷涂料,除去门窗和黑板15.5m2,每平方米涂料需要16元,粉刷这间教室至少需要多少元?
=48+84
=132(m2)
答:粉刷这间教室至少需要1864元。
复习:
8×6+(8×3+6×3)×2
132-15.5=116.5(m2)
16×116.5=1864(元)
2、把一个正方体沿着一个方向锯成3个长方体,它的表面积增加了96平方厘米,那么原正方体的表面积是多少平方厘米?
2×(3-1)=4(面)
96÷4=24(cm2)
24×6=144(cm2)
答:原正方体的表面积是144平方厘米。
长方体(一)
第三课时 露在外面的面
1.结合具体的情境,经历探究多个正方体堆放时露在外面的面的表面积的过程,能够准确地计算出多个正方体堆放时露在外面的面的表面积。
2.观察正方体的堆放,培养学生初步的立体空间想象能力。
3.让学生体会数学知识与现实生活的密切联系,激发学习数学的兴趣。
【难点】能够准确地计算出多个正方体堆放时露在外面的面的表面积。
这样放在墙角有几个面露在外面了?从正面、上面、侧面看它的形状是什么样子的?
正方体一共有几个面?
从正面看:
从右面看:
从上面看:
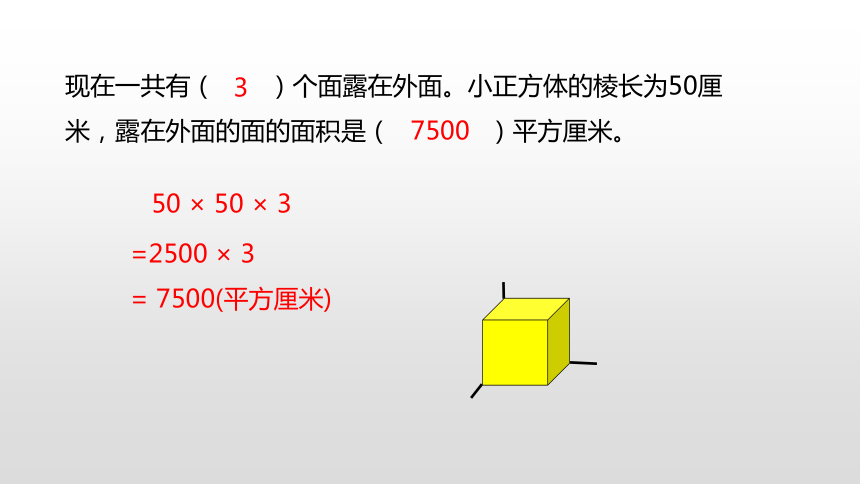
共3个面露在外面。
1
2
3
3
7500
50 × 50 × 3
=2500 × 3
= 7500(平方厘米)
现在一共有( )个面露在外面。小正方体的棱长为50厘米,露在外面的面的面积是( )平方厘米。
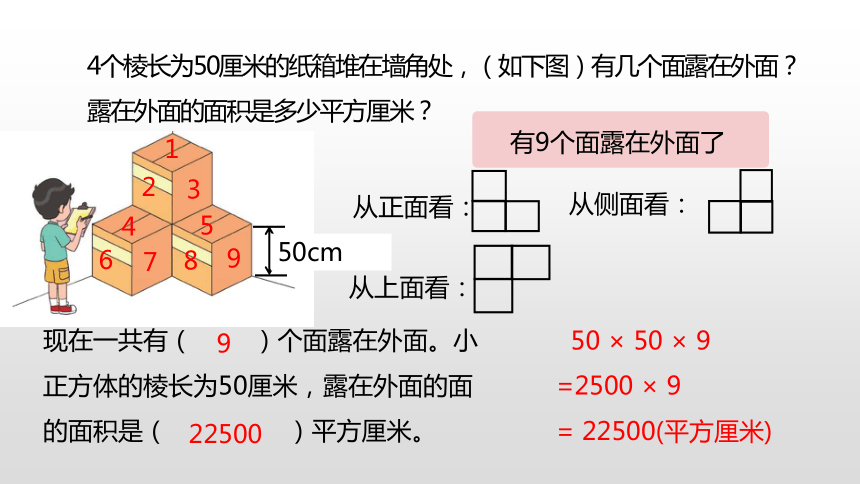
4个棱长为50厘米的纸箱堆在墙角处,(如下图)有几个面露在外面?露在外面的面积是多少平方厘米?
50cm
有9个面露在外面了
1
2
3
4
5
6
7
8
9
从正面看:
从侧面看:
从上面看:
现在一共有( )个面露在外面。小正方体的棱长为50厘米,露在外面的面的面积是( )平方厘米。
9
22500
50 × 50 × 9
=2500 × 9
= 22500(平方厘米)
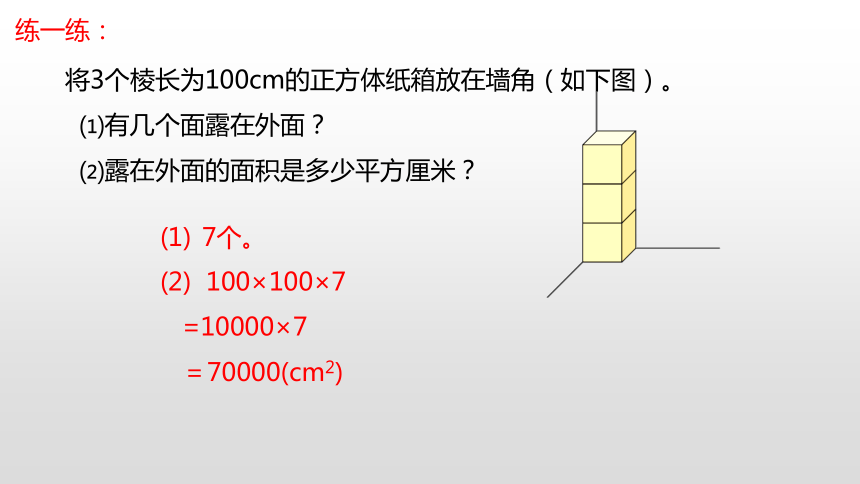
将3个棱长为100cm的正方体纸箱放在墙角(如下图)。
⑴有几个面露在外面?
⑵露在外面的面积是多少平方厘米?
(1) 7个。
(2) 100×100×7
=10000×7
=70000(cm2)
练一练:
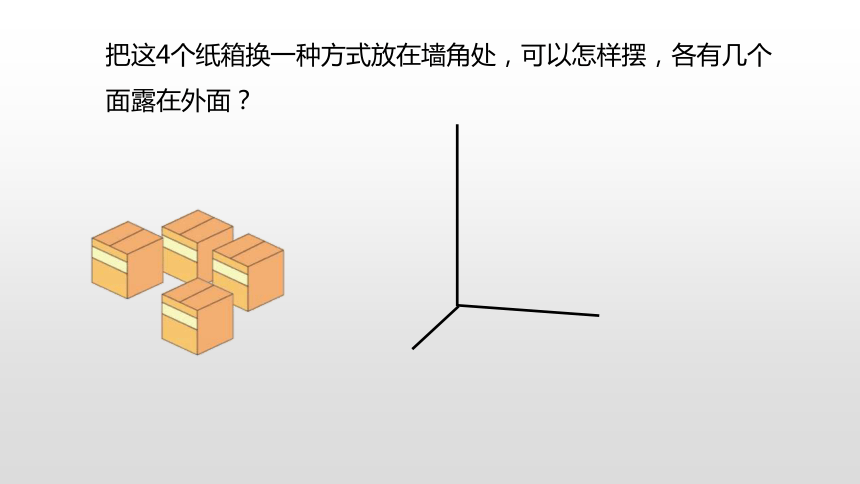
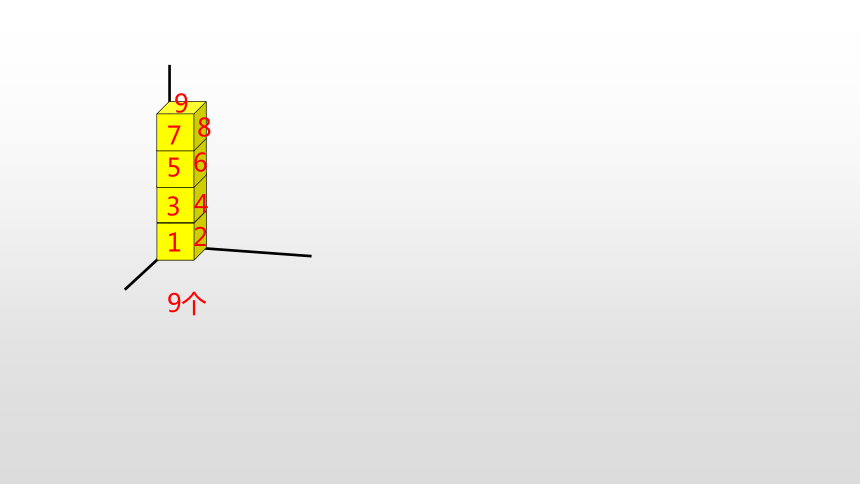
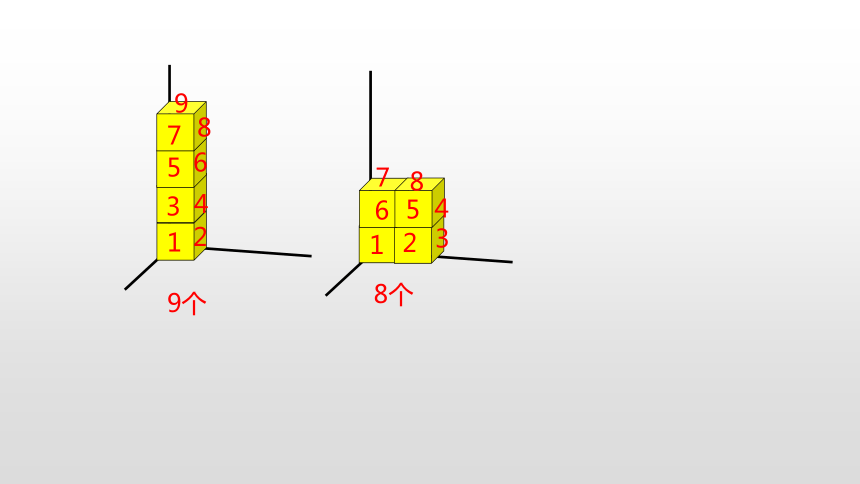
把这4个纸箱换一种方式放在墙角处,可以怎样摆,各有几个面露在外面?
9个
1
2
3
4
5
6
7
8
9
8个
9个
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
8个
9个
8个
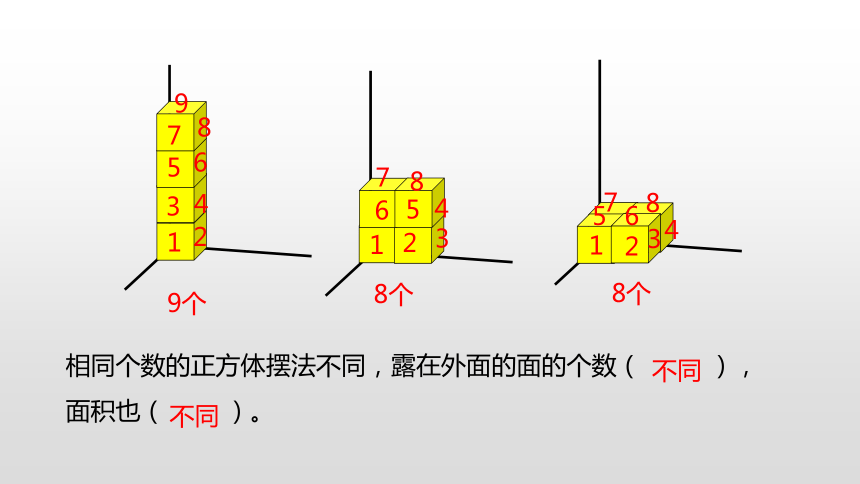
相同个数的正方体摆法不同,露在外面的面的个数( ),面积也( )。
不同
不同
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
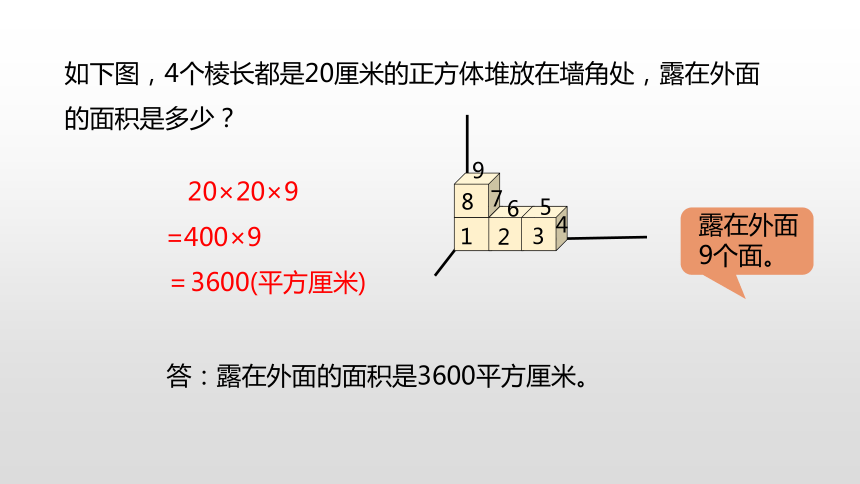
如下图,4个棱长都是20厘米的正方体堆放在墙角处,露在外面的面积是多少?
20×20×9
=400×9
=3600(平方厘米)
答:露在外面的面积是3600平方厘米。
露在外面9个面。
1
2
3
4
5
6
7
8
9
有若干个棱长为5分米的正方体纸盒放在墙角处(如图):
(1)有多少个面露在外面?从正面、侧面、上面分别可以看到什么样的平面图形?
5 ×5 ×10
=25 ×10
=250(平方分米)
练一练:
(2)露在外面的面积是多少平方分米?
从正面看:
从侧面看:
从上面看:
3+3+4=10(个)
答:有10个面露在外面。
答:露在外面的面积是250平方分米。
(1)从正面、侧面、上面分别可以看到什么样的平面图形?有多少个面露在外面?
5+3+5=13(个)
3 ×3 ×13
=9×13
=117(平方分米)
有若干个棱长为3分米的正方体纸盒放在墙角处(如图):
练一练:
从正面看:
从上面看:
从侧面看:
答:有13个面露在外面。
(2)露在外面的面积是多少平方分米?
答:露在外面的面积是117平方分米。
找规律:将小正方体按下图方式摆放在地上,有多少个面露在外面?
1个小正方体有____个面露在外面,
5
2个小正方体有____个面露在外面,
8
3个小正方体有____个面露在外面。
11
按照这样的方式摆放,6个小正方体有 ____个面露在外面。
20
小正方体个数(n)
露在外面的面数
1
2
3
4
5
6
5
8
11
14
17
20
规律:每增加1个小正方体,露在外面的面就增加3个。
求n个正方体露在外面的面数就是求这个数列的末项。
5 + (n - 1)×3=3n+2
末项=首项+(项数-1)×公差
规律:3n+2
练一练:
将25个棱长是2厘米的小正方体按下图方式摆放在桌面上,有多少个面露在外面?露在外面的表面积是多少?
3×25+2=77(个)
2×2×77=308(平方厘米)
答:有77个面露在外面,表面积是308平方厘米。
找规律:将小正方体按下图方式摆放在地上,有多少个面露在外面?
1个小正方体有____个面露在外面,
5
2个小正方体有____个面露在外面,
9
3个小正方体有____个面露在外面。
13
按照这样的方式摆放,6个小正方体有 ____个面露在外面。
25
小正方体的个数 1 2 3 4 5 6
露在外面的面数
5
9
13
17
21
25
你发现了什么规律?
将小正方体按下图方式摆放在地上。
规律:每增加1个小正方体,
露在外面的面就增加4个。
5 + 4 × (n - 1)= 4n+1
规律:4n+1
练一练:
将15个棱长是4厘米的小正方体按下图方式摆放在桌面上,有多少个面露在外面?露在外面的表面积是多少?
4×15+1=61(个)
4×4×61=976(平方厘米)
答:有61个面露在外面,表面积是976平方厘米。
露在外面的面的个数是有规律的。
用n表示正方体的个数:
平放一排 露在外面的面=3n+2
竖放一列 露在外面的面=4n+1
有5个棱长为40cm的正方体放在墙角处。
⑴有几个面露在外面?露在外面的面积是多少平方厘米?
有10个面露在外面
40×40×10
=1600×10
=16000(cm2)
会发生变化
⑵改变摆法,露在外面的面积会发生变化吗?
下图是用8个小正方体拼成的,如果拿走其中的1个,它的表面积会发生变化吗?
不会发生变化。
下图是用27个小正方体拼成的,如果拿走其中的1个,它的表面积会发生变化吗?
从顶点处取走一块,表面积不会发生变化。
从棱上取走一块,表面积会发生变化。
从面上取走一块,表面积会发生变化。
学校运动会的领奖台除了底面不涂漆外,其他各面都涂漆,需要涂漆的面积是多少平方厘米?(单位:cm)
40
100
50
2
1
3
40
100
100
30
40+30=70(厘米)
前后两面:
(40×100+70×100+30×100)×2
=14000×2
=28000(平方厘米)
上面:
100×3×50=15000(平方厘米)
左右面:
70×50×2=7000(平方厘米)
总面积:
28000+15000+7000=50000(平方厘米)
答:需要涂漆的面积是50000平方厘米。
涂黄油漆的面积:
[40×40+40×65+40×(65-10)]×2
=[1600+2600+2200]×2
=[1600+2600+2200]×2
=6400×2
=12800(cm2)
涂红油漆的面积:
40×40×3+65×40×2
=4800+5200
=10000(cm2)
这个颁奖台是由3个长方体合并而成的。它的前后两面涂上油漆,其他露在外面的面涂上红色油漆,涂黄色油漆和涂红色油漆的面积各是多少?
练一练:
把6个棱长3厘米的小正方体拼成一个长方体,它的表面积是多少平方厘米?
方法一
方法二
3 ×6=18(厘米)
18×3 ×4+3 ×3 ×2
=216+18
=234(平方厘米)
把6个棱长3厘米的小正方体拼成一个长方体,它的表面积是多少平方厘米?
方法二
3×3=9(厘米)
3×2=6(厘米)
(9×3+6×3+9×6)×2
=(27+18+54)×2
= 99×2
= 198(平方厘米)
将4个棱长为6cm的正方体拼成一个长方体,长方体的表面积与原来的4个正方体的表面积之和相比,会发生变化吗?变化了多少?
会发生变化
6×6×6
=36×6
=216(cm2)
将小正方体拼成一个大长方体,减少了6个面。
表面积减少了216平方厘米。
布置作业:
练习册第15页1--5题;第16页1--5题。
1、一间教室长8m、宽6m、高3m。要给教室的墙壁和房顶粉刷涂料,除去门窗和黑板15.5m2,每平方米涂料需要16元,粉刷这间教室至少需要多少元?
=48+84
=132(m2)
答:粉刷这间教室至少需要1864元。
复习:
8×6+(8×3+6×3)×2
132-15.5=116.5(m2)
16×116.5=1864(元)
2、把一个正方体沿着一个方向锯成3个长方体,它的表面积增加了96平方厘米,那么原正方体的表面积是多少平方厘米?
2×(3-1)=4(面)
96÷4=24(cm2)
24×6=144(cm2)
答:原正方体的表面积是144平方厘米。
长方体(一)
第三课时 露在外面的面
1.结合具体的情境,经历探究多个正方体堆放时露在外面的面的表面积的过程,能够准确地计算出多个正方体堆放时露在外面的面的表面积。
2.观察正方体的堆放,培养学生初步的立体空间想象能力。
3.让学生体会数学知识与现实生活的密切联系,激发学习数学的兴趣。
【难点】能够准确地计算出多个正方体堆放时露在外面的面的表面积。
这样放在墙角有几个面露在外面了?从正面、上面、侧面看它的形状是什么样子的?
正方体一共有几个面?
从正面看:
从右面看:
从上面看:
共3个面露在外面。
1
2
3
3
7500
50 × 50 × 3
=2500 × 3
= 7500(平方厘米)
现在一共有( )个面露在外面。小正方体的棱长为50厘米,露在外面的面的面积是( )平方厘米。
4个棱长为50厘米的纸箱堆在墙角处,(如下图)有几个面露在外面?露在外面的面积是多少平方厘米?
50cm
有9个面露在外面了
1
2
3
4
5
6
7
8
9
从正面看:
从侧面看:
从上面看:
现在一共有( )个面露在外面。小正方体的棱长为50厘米,露在外面的面的面积是( )平方厘米。
9
22500
50 × 50 × 9
=2500 × 9
= 22500(平方厘米)
将3个棱长为100cm的正方体纸箱放在墙角(如下图)。
⑴有几个面露在外面?
⑵露在外面的面积是多少平方厘米?
(1) 7个。
(2) 100×100×7
=10000×7
=70000(cm2)
练一练:
把这4个纸箱换一种方式放在墙角处,可以怎样摆,各有几个面露在外面?
9个
1
2
3
4
5
6
7
8
9
8个
9个
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
8个
9个
8个
相同个数的正方体摆法不同,露在外面的面的个数( ),面积也( )。
不同
不同
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
如下图,4个棱长都是20厘米的正方体堆放在墙角处,露在外面的面积是多少?
20×20×9
=400×9
=3600(平方厘米)
答:露在外面的面积是3600平方厘米。
露在外面9个面。
1
2
3
4
5
6
7
8
9
有若干个棱长为5分米的正方体纸盒放在墙角处(如图):
(1)有多少个面露在外面?从正面、侧面、上面分别可以看到什么样的平面图形?
5 ×5 ×10
=25 ×10
=250(平方分米)
练一练:
(2)露在外面的面积是多少平方分米?
从正面看:
从侧面看:
从上面看:
3+3+4=10(个)
答:有10个面露在外面。
答:露在外面的面积是250平方分米。
(1)从正面、侧面、上面分别可以看到什么样的平面图形?有多少个面露在外面?
5+3+5=13(个)
3 ×3 ×13
=9×13
=117(平方分米)
有若干个棱长为3分米的正方体纸盒放在墙角处(如图):
练一练:
从正面看:
从上面看:
从侧面看:
答:有13个面露在外面。
(2)露在外面的面积是多少平方分米?
答:露在外面的面积是117平方分米。
找规律:将小正方体按下图方式摆放在地上,有多少个面露在外面?
1个小正方体有____个面露在外面,
5
2个小正方体有____个面露在外面,
8
3个小正方体有____个面露在外面。
11
按照这样的方式摆放,6个小正方体有 ____个面露在外面。
20
小正方体个数(n)
露在外面的面数
1
2
3
4
5
6
5
8
11
14
17
20
规律:每增加1个小正方体,露在外面的面就增加3个。
求n个正方体露在外面的面数就是求这个数列的末项。
5 + (n - 1)×3=3n+2
末项=首项+(项数-1)×公差
规律:3n+2
练一练:
将25个棱长是2厘米的小正方体按下图方式摆放在桌面上,有多少个面露在外面?露在外面的表面积是多少?
3×25+2=77(个)
2×2×77=308(平方厘米)
答:有77个面露在外面,表面积是308平方厘米。
找规律:将小正方体按下图方式摆放在地上,有多少个面露在外面?
1个小正方体有____个面露在外面,
5
2个小正方体有____个面露在外面,
9
3个小正方体有____个面露在外面。
13
按照这样的方式摆放,6个小正方体有 ____个面露在外面。
25
小正方体的个数 1 2 3 4 5 6
露在外面的面数
5
9
13
17
21
25
你发现了什么规律?
将小正方体按下图方式摆放在地上。
规律:每增加1个小正方体,
露在外面的面就增加4个。
5 + 4 × (n - 1)= 4n+1
规律:4n+1
练一练:
将15个棱长是4厘米的小正方体按下图方式摆放在桌面上,有多少个面露在外面?露在外面的表面积是多少?
4×15+1=61(个)
4×4×61=976(平方厘米)
答:有61个面露在外面,表面积是976平方厘米。
露在外面的面的个数是有规律的。
用n表示正方体的个数:
平放一排 露在外面的面=3n+2
竖放一列 露在外面的面=4n+1
有5个棱长为40cm的正方体放在墙角处。
⑴有几个面露在外面?露在外面的面积是多少平方厘米?
有10个面露在外面
40×40×10
=1600×10
=16000(cm2)
会发生变化
⑵改变摆法,露在外面的面积会发生变化吗?
下图是用8个小正方体拼成的,如果拿走其中的1个,它的表面积会发生变化吗?
不会发生变化。
下图是用27个小正方体拼成的,如果拿走其中的1个,它的表面积会发生变化吗?
从顶点处取走一块,表面积不会发生变化。
从棱上取走一块,表面积会发生变化。
从面上取走一块,表面积会发生变化。
学校运动会的领奖台除了底面不涂漆外,其他各面都涂漆,需要涂漆的面积是多少平方厘米?(单位:cm)
40
100
50
2
1
3
40
100
100
30
40+30=70(厘米)
前后两面:
(40×100+70×100+30×100)×2
=14000×2
=28000(平方厘米)
上面:
100×3×50=15000(平方厘米)
左右面:
70×50×2=7000(平方厘米)
总面积:
28000+15000+7000=50000(平方厘米)
答:需要涂漆的面积是50000平方厘米。
涂黄油漆的面积:
[40×40+40×65+40×(65-10)]×2
=[1600+2600+2200]×2
=[1600+2600+2200]×2
=6400×2
=12800(cm2)
涂红油漆的面积:
40×40×3+65×40×2
=4800+5200
=10000(cm2)
这个颁奖台是由3个长方体合并而成的。它的前后两面涂上油漆,其他露在外面的面涂上红色油漆,涂黄色油漆和涂红色油漆的面积各是多少?
练一练:
把6个棱长3厘米的小正方体拼成一个长方体,它的表面积是多少平方厘米?
方法一
方法二
3 ×6=18(厘米)
18×3 ×4+3 ×3 ×2
=216+18
=234(平方厘米)
把6个棱长3厘米的小正方体拼成一个长方体,它的表面积是多少平方厘米?
方法二
3×3=9(厘米)
3×2=6(厘米)
(9×3+6×3+9×6)×2
=(27+18+54)×2
= 99×2
= 198(平方厘米)
将4个棱长为6cm的正方体拼成一个长方体,长方体的表面积与原来的4个正方体的表面积之和相比,会发生变化吗?变化了多少?
会发生变化
6×6×6
=36×6
=216(cm2)
将小正方体拼成一个大长方体,减少了6个面。
表面积减少了216平方厘米。
布置作业:
练习册第15页1--5题;第16页1--5题。
