四年级下册数学北师大版三角形内角和课件(共47张PPT)
文档属性
| 名称 | 四年级下册数学北师大版三角形内角和课件(共47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-13 00:00:00 | ||
图片预览






文档简介
(共47张PPT)
(1)只要有两个角是锐角的三角形,就一定是锐角三角形。( )
(2)等边三角形和等腰三角形一定是锐角三角形。 ( )
(3)直角三角形中最大角的度数是90°。 ( )
(4)等腰三角形一定是等边三角形。 ( )
(5)只要有一个角是钝角的三角形就是钝角三角形。 ( )
(6)等腰三角形的两个底角一定相等。 ( )
判断题。(对的画“√”,错的画“×”。)
×
×
√
×
复习:
√
√
认识三角形和四边形
探索与发现:三角形内角和(1)
北师大版 数学 四年级 下册
我个头大,我的三个内角的和一定比你的大。
是这样的吗?
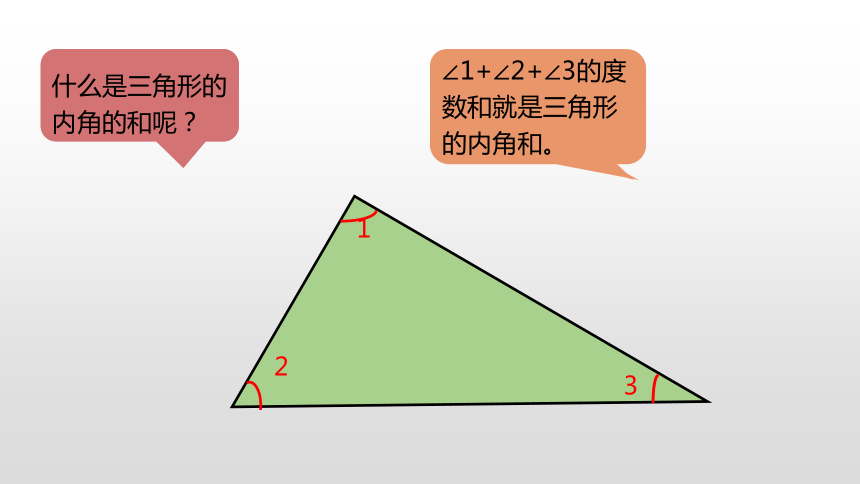
什么是三角形的内角的和呢?
1
2
3
什么是三角形的内角呢?
∠1、∠2和∠3就是三角形的内角。
什么是三角形的内角的和呢?
∠1+∠2+∠3的度数和就是三角形的内角和。
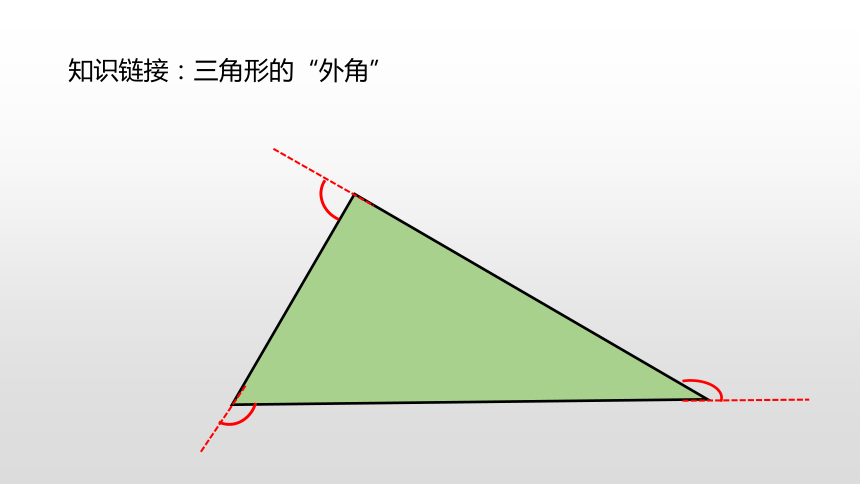
知识链接:三角形的“外角”
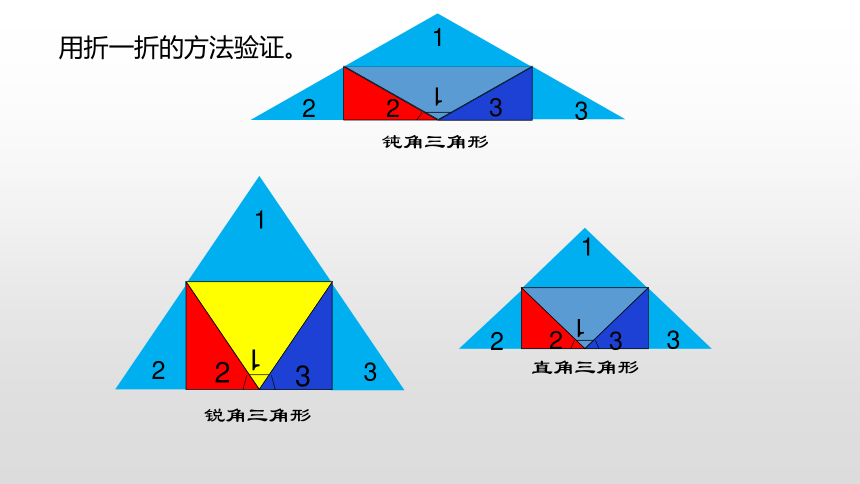
锐角三角形
直角三角形
钝角三角形
1
2
3
1
1
2
2
3
3
三角形的内角和是多少度呢?
我们学过量角,我可以用量角器量一量,算一算。
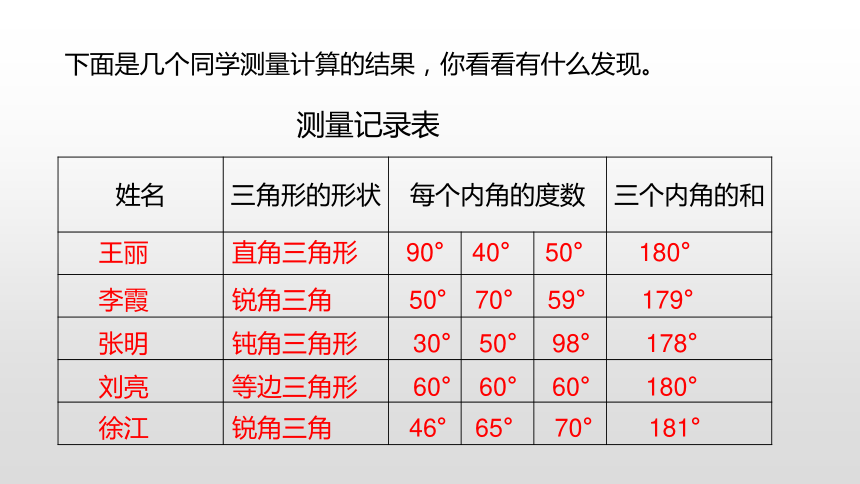
下面是几个同学测量计算的结果,你看看有什么发现。
姓名 三角形的形状 每个内角的度数 三个内角的和
测量记录表
王丽 直角三角形 90° 40° 50° 180°
李霞 锐角三角 50° 70° 59° 179°
张明 钝角三角形 30° 50° 98° 178°
刘亮 等边三角形 60° 60° 60° 180°
徐江 锐角三角 46° 65° 70° 181°
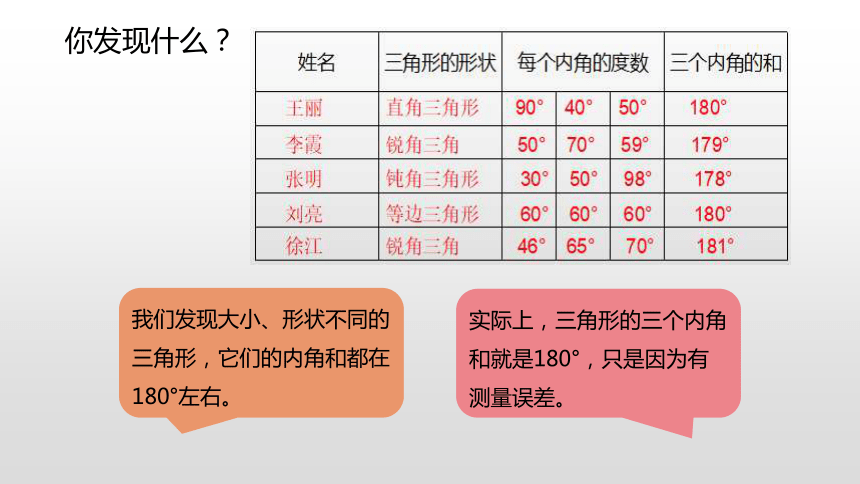
你发现什么?
我们发现大小、形状不同的三角形,它们的内角和都在180°左右。
实际上,三角形的三个内角和就是180°,只是因为有测量误差。
有什么方法能验证三角形内角和是180°这个猜想呢?
三个角拼在一起呈180°的平角。
2
1
2
2
3
3
钝角三角形
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
1
用折一折的方法验证。
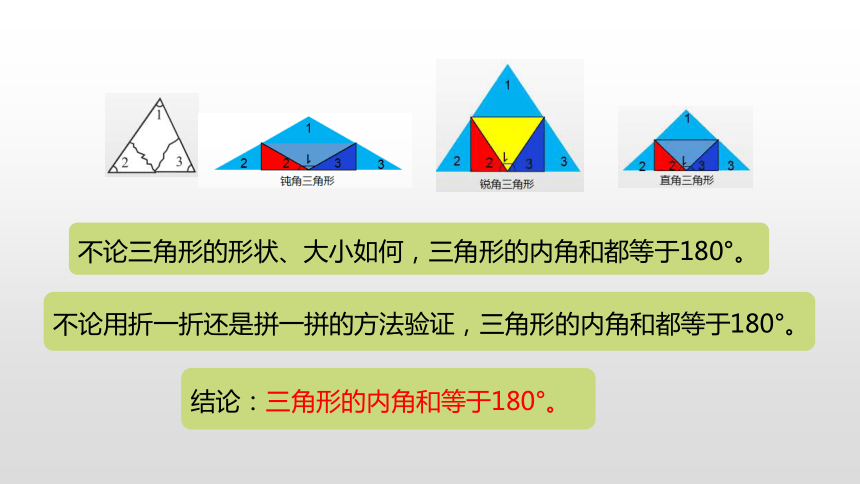
不论三角形的形状、大小如何,三角形的内角和都等于180°。
不论用折一折还是拼一拼的方法验证,三角形的内角和都等于180°。
结论:三角形的内角和等于180°。
判一判。(对的画“√”,错的画“×”)
(1)三角形越大,内角和就越大。 ( )
(2)一个三角形的三个内角度数是: 54° 、56° 、 70° 。( )
(2)大三角形比小三角形的内角和大。 ( )
(3)两个小三角形拼成一个大三角形, 大三角形的内角和是360°
( )
√
×
×
×
不论三角形的形状、大小,三角形的内角和都等于180°。
选一选。
(1)把一个三角形的三个内角拼在一起,可以组成一个( )。
A.直角 B.钝角 C.平角
(2)用一个放大10倍的放大镜看一个三角形,这个三角形的内角和是( )。
A.1800° B.180° C.90°
C
B
填一填。
(1)一个三角形的内角和是( ),把三角形的每条边都扩大到原来的5倍后,这个三角形的内角和是( )。
(2)两个相同的小三角形拼成一个大三角形,这个大三角形的内角和是( )。
(3)把一个三角形的三个内角拼在一起,可以拼成一个( )角。
180°
180°
180°
平
在一个直角三角形中,如果一个锐角是36°,另一个角可以是64°吗?为什么?
90°+36°+64°=190°
答:另一个角不可以是64°。
方法一:
190°>180°
方法二:
180°-36°-90°=54°
54°>64°
在一个直角三角形中,如果一个锐角是32°,另一个角是多少度?
答:另一个角是58°。
180°-32°-90°=58°
练一练:
猜一猜,可能是什么三角形呢?
根据三角形内角和是180°,可以求出被遮住的角的度数。
180°-60°-40°=80°
因为三角形三个角的度数是60°、40°和80°,所以这个三角形是锐角三角形。
猜一猜,可能是什么三角形?
猜一猜,你还能猜出是什么三角形?
已知一个角是60°,另外两个角都被遮住,要判断这是一个什么三角形需要知道另外两个角的度数。
猜一猜,你还能猜出是什么三角形?
根据三角形内角和是180°,剩下的两个角的度数和应该是180°-60°=120°。
猜一猜,你还能猜出是什么三角形?
钝角+锐角=120°,这个三角形就是钝角三角形;
锐角+锐角=120°,这个三角形就是锐角三角形;
90°+30°=120°,这个三角形就是直角三角形。
答:这个三角形可能是钝角三角形、直角三角形、锐角三角形。
(1)∠ 1=30 ° , ∠ 2=80 ° , ∠3 =( ) °,是( )三角形。
求下面各三角形中∠3的度数。
(2)∠ 1=44° , ∠ 2=33° , ∠3 =( ) °,是( )三角形。
(3)∠ 1= 43°,∠ 2=47° , ∠3 =( ) °,是( )三角形。
70
锐角
103
钝角
90
直角
(1)一个三角形中有一个锐角,这个三角形一定是锐角三角形。( )
(2)三角形的一个角是105°,这个三角形一定是钝角三角形。 ( )
(3)一个直角三角形的一个锐角是60°,则另一个锐角是30°。 ( )
判一判。(对的画“√”,错的画“×” )
√
√
三角形中有一个锐角,这个三角形有可能是锐角三角形、直角三角形或是钝角三角形。
4
填出下面各角的度数。
77°
55°
115°
既是直角三角形
又是等腰三角形
等腰直角三角形
等腰直角三角形的两个底角都是45°。
注意:
1、三角形内角和等于180°。
2、等腰三角形的两个底角一定相等。
3、等边三角形的三个角相等,每个角都是60°
4、既是直角三角形又是等腰三角形的三角形叫“等腰直角三角形”。
已知一个等腰三角形的底角是72度,顶角是多少度?
180°-72°-72 = 36°
72°
72°
?
答:顶角是36°。
等腰三角形的底角有2个。
等腰三角形的2个底角相等。
已知一个等腰三角形的顶角是100度,底角是多少度?
(180°-100°)÷2 = 40°
答:底角是40°。
等腰三角形的底角有2个。
等腰三角形的2个底角相等。
练一练:
已知一个等腰三角形的顶角度数是底角度数的2倍,那么顶角和底角分别是多少度?这是一个什么类型的三角形?
180°÷(1+1+2) = 45°
答:顶角是90°,底角是45°。它是一个等腰直角三角形。
底角度数看做1份,顶角度数就是2份。
等腰三角形的2个底角相等,那么三角形的三个内角一共是1+1+2等于4份。
45°×2 = 90°
已知一个等腰三角形的底角度数是顶角度数的4倍,那么顶角和底角分别是多少度?按角分是一个什么类型的三角形?
180°÷(4+4+1) = 20°
答:顶角是20°,底角是80°。它是一个锐角三角形。
顶角度数看做1份,底角度数就是4份。
等腰三角形的2个底角相等,那么三角形的三个内角一共是4+4+1等于9份。
20°×4 = 80°
练一练:
如图,用两把完全相同的三角尺分别拼出一个四边形和一个三角形。
想一想,它们的内角和分别是多少?与同伴交流你是怎么想的。
的内角和是360°,因为 的内角和是两个三角形的内角和相加等于360°。
的内角和是180°,因为三角形的内角之和等于180°。
180°×3 = 540°
如图,五边形的内角和是多少度?
因为三角形的内角和是180°,用分割法将五边形分割成若干个三角形。
70°
112°
50°
60°
52°
48°
80°
36
下面哪三个角能构成一个三角形
(1) (2)
50°+70°+60°=180°
52°+48°+80°=180°
50°、70°和60°能构成一个三角形。
52°、48°和80°能构成一个三角形。
三角形内角和等于180°。
在求三角形内角和度数时,可以采用拼剪和折拼的转化方法。
(1)把一个三角形剪成两个小三角形,每个小三角形的内角和是( )。
A.90° B.180° C.360°
(2)下面的各组的度数能组成三角形的是( )。
A.34° 、86°、70° B.120°、32°、28° C.55°、52°、65°
选一选。
三角形的内角和等于180°。
B
B
下面各角的度数能拼成三角形的有几组?写一写。(不能重复使用)
43°
97°
59°
89°
40°
32°
43°+97°+40°=180°
59°+89°+32°=180°
答:43°、97°和40°能拼成一个三角形,59°、89°和32°能拼成一个三角形。
下面是小红测量的三角形各个角的度数,她测量的对吗?为什么?
80°
50°
40°
50°+80°+40°=170°
因为三角形的内角和等于180°,所以小红测量的不对。
1.已知三角形两个角的度数,会求出第三个角的度数。
2.运用所学知识解决简单的实际问题。
【重点】应用三角形的内角和求未知角。
【难点】应用三角形的内角和解决实际问题。
选一选。
(1)一个三角形的两个内角分别是55°和54°, 则这个三角形是( )三角形。
A.锐角 B.直角 C.钝角
(2)一个三角形中,最大的角的度数等于其余两个角的度数之和,这个三角形一定是( )三角形。
A.锐角 B.直角 C.钝角
A
B
3
量一量,猜一猜,可能是什么三角形?
5
被遮住的三角形一定是钝角三角形
露出的一个角是钝角。
5
量一量,猜一猜,按角分类,这个三角形可能是什么三角形?
只知道三角形的一个角是锐角。
被遮住的三角形可能是锐角三角形
有可能藏起来的两个角相等。
6
量一量,猜一猜,按角分类,这个三角形可能是什么三角形?
180°-45°-45°=90°
答:这个三角形是直角三角形。
45°
45°
已知一个等腰三角形 (如下图所示),∠1的度数是多少?
∠1=180°-72°-72 = 36°
72°
72°
∠1
7
答:∠1的度数是是36°。
已知三角形中两个角的度数,根据三角形内角和等于180°可以求出第三个角的度数,从而判断该三角形是什么三角形。
已知三角形的一个角的度数,根据三角形内角和等于180°可以求出两外两个角的度数之和,再判断该三角形是什么三角形。
它们说的对吗?
1
我的两个锐角之和大于90°。
我的两个锐角之和正好等于90°。
180°减去一个钝角不可能等于钝角,钝角三角形的说法不正确。
180°减去一个直角等于90°,直角三角形的说法正确。
在一个直角三角形中,另外两个内角可能是多少度?
可能是:90 ° +( ) ° +( ) °
2
另外两个角的和是:180°-90°=90°。
35
55
(答案不唯一)
下面图形中被遮住的角是多少度
180 °-114°- 34 °= 32 °
3
34°
114°
答:被遮住的角是32°。
(1)只要有两个角是锐角的三角形,就一定是锐角三角形。( )
(2)等边三角形和等腰三角形一定是锐角三角形。 ( )
(3)直角三角形中最大角的度数是90°。 ( )
(4)等腰三角形一定是等边三角形。 ( )
(5)只要有一个角是钝角的三角形就是钝角三角形。 ( )
(6)等腰三角形的两个底角一定相等。 ( )
判断题。(对的画“√”,错的画“×”。)
×
×
√
×
复习:
√
√
认识三角形和四边形
探索与发现:三角形内角和(1)
北师大版 数学 四年级 下册
我个头大,我的三个内角的和一定比你的大。
是这样的吗?
什么是三角形的内角的和呢?
1
2
3
什么是三角形的内角呢?
∠1、∠2和∠3就是三角形的内角。
什么是三角形的内角的和呢?
∠1+∠2+∠3的度数和就是三角形的内角和。
知识链接:三角形的“外角”
锐角三角形
直角三角形
钝角三角形
1
2
3
1
1
2
2
3
3
三角形的内角和是多少度呢?
我们学过量角,我可以用量角器量一量,算一算。
下面是几个同学测量计算的结果,你看看有什么发现。
姓名 三角形的形状 每个内角的度数 三个内角的和
测量记录表
王丽 直角三角形 90° 40° 50° 180°
李霞 锐角三角 50° 70° 59° 179°
张明 钝角三角形 30° 50° 98° 178°
刘亮 等边三角形 60° 60° 60° 180°
徐江 锐角三角 46° 65° 70° 181°
你发现什么?
我们发现大小、形状不同的三角形,它们的内角和都在180°左右。
实际上,三角形的三个内角和就是180°,只是因为有测量误差。
有什么方法能验证三角形内角和是180°这个猜想呢?
三个角拼在一起呈180°的平角。
2
1
2
2
3
3
钝角三角形
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
1
用折一折的方法验证。
不论三角形的形状、大小如何,三角形的内角和都等于180°。
不论用折一折还是拼一拼的方法验证,三角形的内角和都等于180°。
结论:三角形的内角和等于180°。
判一判。(对的画“√”,错的画“×”)
(1)三角形越大,内角和就越大。 ( )
(2)一个三角形的三个内角度数是: 54° 、56° 、 70° 。( )
(2)大三角形比小三角形的内角和大。 ( )
(3)两个小三角形拼成一个大三角形, 大三角形的内角和是360°
( )
√
×
×
×
不论三角形的形状、大小,三角形的内角和都等于180°。
选一选。
(1)把一个三角形的三个内角拼在一起,可以组成一个( )。
A.直角 B.钝角 C.平角
(2)用一个放大10倍的放大镜看一个三角形,这个三角形的内角和是( )。
A.1800° B.180° C.90°
C
B
填一填。
(1)一个三角形的内角和是( ),把三角形的每条边都扩大到原来的5倍后,这个三角形的内角和是( )。
(2)两个相同的小三角形拼成一个大三角形,这个大三角形的内角和是( )。
(3)把一个三角形的三个内角拼在一起,可以拼成一个( )角。
180°
180°
180°
平
在一个直角三角形中,如果一个锐角是36°,另一个角可以是64°吗?为什么?
90°+36°+64°=190°
答:另一个角不可以是64°。
方法一:
190°>180°
方法二:
180°-36°-90°=54°
54°>64°
在一个直角三角形中,如果一个锐角是32°,另一个角是多少度?
答:另一个角是58°。
180°-32°-90°=58°
练一练:
猜一猜,可能是什么三角形呢?
根据三角形内角和是180°,可以求出被遮住的角的度数。
180°-60°-40°=80°
因为三角形三个角的度数是60°、40°和80°,所以这个三角形是锐角三角形。
猜一猜,可能是什么三角形?
猜一猜,你还能猜出是什么三角形?
已知一个角是60°,另外两个角都被遮住,要判断这是一个什么三角形需要知道另外两个角的度数。
猜一猜,你还能猜出是什么三角形?
根据三角形内角和是180°,剩下的两个角的度数和应该是180°-60°=120°。
猜一猜,你还能猜出是什么三角形?
钝角+锐角=120°,这个三角形就是钝角三角形;
锐角+锐角=120°,这个三角形就是锐角三角形;
90°+30°=120°,这个三角形就是直角三角形。
答:这个三角形可能是钝角三角形、直角三角形、锐角三角形。
(1)∠ 1=30 ° , ∠ 2=80 ° , ∠3 =( ) °,是( )三角形。
求下面各三角形中∠3的度数。
(2)∠ 1=44° , ∠ 2=33° , ∠3 =( ) °,是( )三角形。
(3)∠ 1= 43°,∠ 2=47° , ∠3 =( ) °,是( )三角形。
70
锐角
103
钝角
90
直角
(1)一个三角形中有一个锐角,这个三角形一定是锐角三角形。( )
(2)三角形的一个角是105°,这个三角形一定是钝角三角形。 ( )
(3)一个直角三角形的一个锐角是60°,则另一个锐角是30°。 ( )
判一判。(对的画“√”,错的画“×” )
√
√
三角形中有一个锐角,这个三角形有可能是锐角三角形、直角三角形或是钝角三角形。
4
填出下面各角的度数。
77°
55°
115°
既是直角三角形
又是等腰三角形
等腰直角三角形
等腰直角三角形的两个底角都是45°。
注意:
1、三角形内角和等于180°。
2、等腰三角形的两个底角一定相等。
3、等边三角形的三个角相等,每个角都是60°
4、既是直角三角形又是等腰三角形的三角形叫“等腰直角三角形”。
已知一个等腰三角形的底角是72度,顶角是多少度?
180°-72°-72 = 36°
72°
72°
?
答:顶角是36°。
等腰三角形的底角有2个。
等腰三角形的2个底角相等。
已知一个等腰三角形的顶角是100度,底角是多少度?
(180°-100°)÷2 = 40°
答:底角是40°。
等腰三角形的底角有2个。
等腰三角形的2个底角相等。
练一练:
已知一个等腰三角形的顶角度数是底角度数的2倍,那么顶角和底角分别是多少度?这是一个什么类型的三角形?
180°÷(1+1+2) = 45°
答:顶角是90°,底角是45°。它是一个等腰直角三角形。
底角度数看做1份,顶角度数就是2份。
等腰三角形的2个底角相等,那么三角形的三个内角一共是1+1+2等于4份。
45°×2 = 90°
已知一个等腰三角形的底角度数是顶角度数的4倍,那么顶角和底角分别是多少度?按角分是一个什么类型的三角形?
180°÷(4+4+1) = 20°
答:顶角是20°,底角是80°。它是一个锐角三角形。
顶角度数看做1份,底角度数就是4份。
等腰三角形的2个底角相等,那么三角形的三个内角一共是4+4+1等于9份。
20°×4 = 80°
练一练:
如图,用两把完全相同的三角尺分别拼出一个四边形和一个三角形。
想一想,它们的内角和分别是多少?与同伴交流你是怎么想的。
的内角和是360°,因为 的内角和是两个三角形的内角和相加等于360°。
的内角和是180°,因为三角形的内角之和等于180°。
180°×3 = 540°
如图,五边形的内角和是多少度?
因为三角形的内角和是180°,用分割法将五边形分割成若干个三角形。
70°
112°
50°
60°
52°
48°
80°
36
下面哪三个角能构成一个三角形
(1) (2)
50°+70°+60°=180°
52°+48°+80°=180°
50°、70°和60°能构成一个三角形。
52°、48°和80°能构成一个三角形。
三角形内角和等于180°。
在求三角形内角和度数时,可以采用拼剪和折拼的转化方法。
(1)把一个三角形剪成两个小三角形,每个小三角形的内角和是( )。
A.90° B.180° C.360°
(2)下面的各组的度数能组成三角形的是( )。
A.34° 、86°、70° B.120°、32°、28° C.55°、52°、65°
选一选。
三角形的内角和等于180°。
B
B
下面各角的度数能拼成三角形的有几组?写一写。(不能重复使用)
43°
97°
59°
89°
40°
32°
43°+97°+40°=180°
59°+89°+32°=180°
答:43°、97°和40°能拼成一个三角形,59°、89°和32°能拼成一个三角形。
下面是小红测量的三角形各个角的度数,她测量的对吗?为什么?
80°
50°
40°
50°+80°+40°=170°
因为三角形的内角和等于180°,所以小红测量的不对。
1.已知三角形两个角的度数,会求出第三个角的度数。
2.运用所学知识解决简单的实际问题。
【重点】应用三角形的内角和求未知角。
【难点】应用三角形的内角和解决实际问题。
选一选。
(1)一个三角形的两个内角分别是55°和54°, 则这个三角形是( )三角形。
A.锐角 B.直角 C.钝角
(2)一个三角形中,最大的角的度数等于其余两个角的度数之和,这个三角形一定是( )三角形。
A.锐角 B.直角 C.钝角
A
B
3
量一量,猜一猜,可能是什么三角形?
5
被遮住的三角形一定是钝角三角形
露出的一个角是钝角。
5
量一量,猜一猜,按角分类,这个三角形可能是什么三角形?
只知道三角形的一个角是锐角。
被遮住的三角形可能是锐角三角形
有可能藏起来的两个角相等。
6
量一量,猜一猜,按角分类,这个三角形可能是什么三角形?
180°-45°-45°=90°
答:这个三角形是直角三角形。
45°
45°
已知一个等腰三角形 (如下图所示),∠1的度数是多少?
∠1=180°-72°-72 = 36°
72°
72°
∠1
7
答:∠1的度数是是36°。
已知三角形中两个角的度数,根据三角形内角和等于180°可以求出第三个角的度数,从而判断该三角形是什么三角形。
已知三角形的一个角的度数,根据三角形内角和等于180°可以求出两外两个角的度数之和,再判断该三角形是什么三角形。
它们说的对吗?
1
我的两个锐角之和大于90°。
我的两个锐角之和正好等于90°。
180°减去一个钝角不可能等于钝角,钝角三角形的说法不正确。
180°减去一个直角等于90°,直角三角形的说法正确。
在一个直角三角形中,另外两个内角可能是多少度?
可能是:90 ° +( ) ° +( ) °
2
另外两个角的和是:180°-90°=90°。
35
55
(答案不唯一)
下面图形中被遮住的角是多少度
180 °-114°- 34 °= 32 °
3
34°
114°
答:被遮住的角是32°。
