四年级下册数学北师大版三角形三边的关系课件(共37张PPT)
文档属性
| 名称 | 四年级下册数学北师大版三角形三边的关系课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 539.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-13 00:00:00 | ||
图片预览




文档简介
(共37张PPT)
1、填一填。
(1)一个三角形的内角和是( ),把三角形的每条边都扩大到原来的5倍后,这个三角形的内角和是( )。
(2)两个相同的小三角形拼成一个大三角形,这个大三角形的内角和是( )。
180°
180°
180°
2、已知一个等腰三角形的底角是72度,顶角是多少度?
180°-72°-72 = 36°
3、已知一个等腰三角形的顶角度数是底角度数的2倍,那么顶角和底角分别是多少度?这是一个什么类型的三角形?
180°÷(1+1+2) = 45°
45°×2 = 90°
答:顶角是90°,底角是45°。它是一个等腰直角三角形。
答:顶角是36°。
复习:
认识三角形和四边形
三角形边的关系
北师大版 数学 四年级 下册
给你3根小棒,你能用它们围一个三角形吗?
只要给你3根小棒,你就能用它们围一个三角形吗?
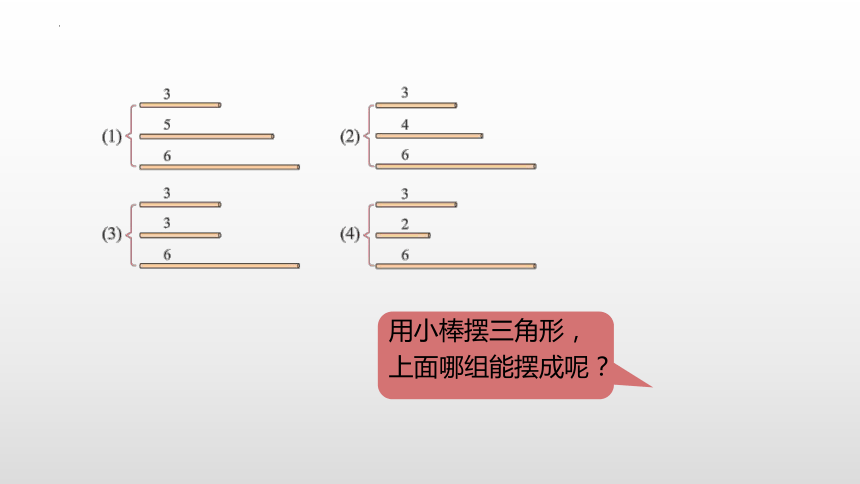
用小棒摆三角形,上面哪组能摆成呢?
算一算:每两边之和与第三边的关系
3cm
5cm
6cm
(1)
5cm
3cm
5cm
3cm
5cm
3cm
6cm
第(1)组小棒能摆成三角形。
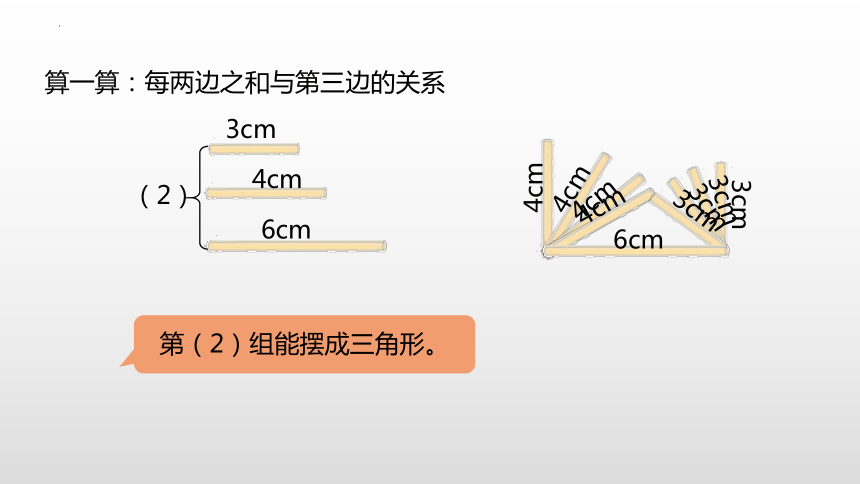
算一算:每两边之和与第三边的关系
3cm
4cm
6cm
(2)
4cm
3cm
4cm
3cm
4cm
3cm
4cm
3cm
6cm
第(2)组能摆成三角形。
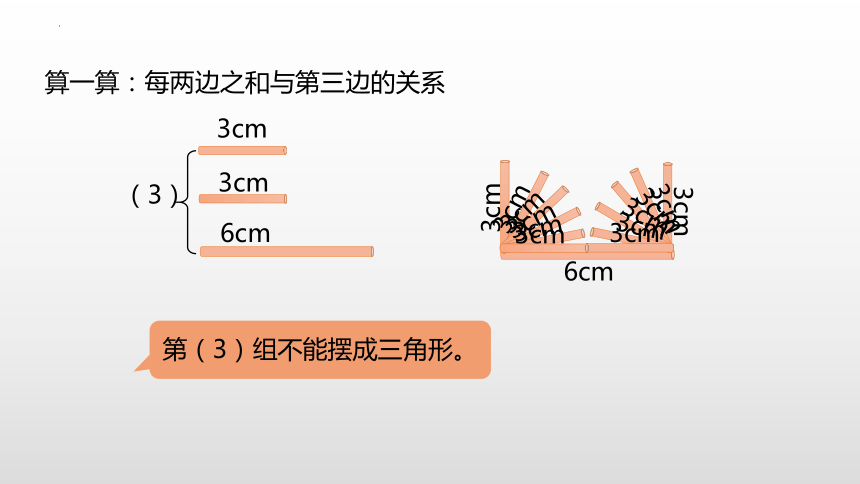
算一算:每两边之和与第三边的关系
3cm
3cm
6cm
(3)
6cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
第(3)组不能摆成三角形。
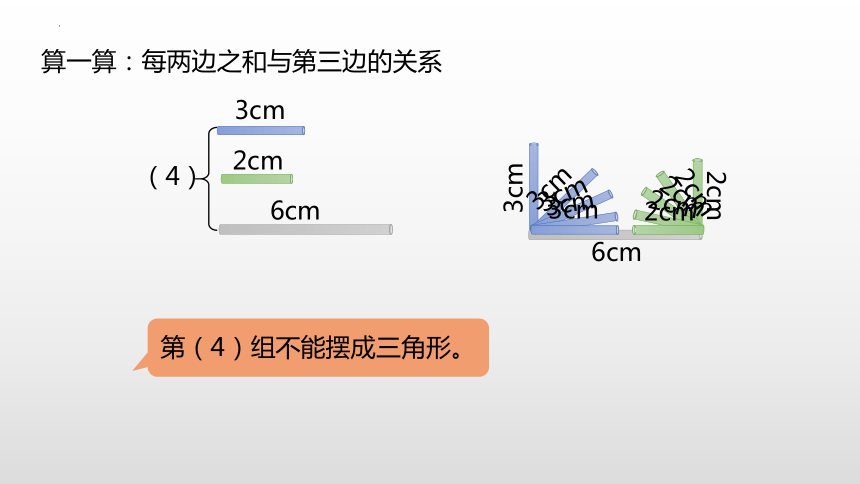
算一算:每两边之和与第三边的关系
3cm
2cm
6cm
(4)
6cm
3cm
2cm
3cm
2cm
3cm
2cm
3cm
2cm
3cm
2cm
第(4)组不能摆成三角形。
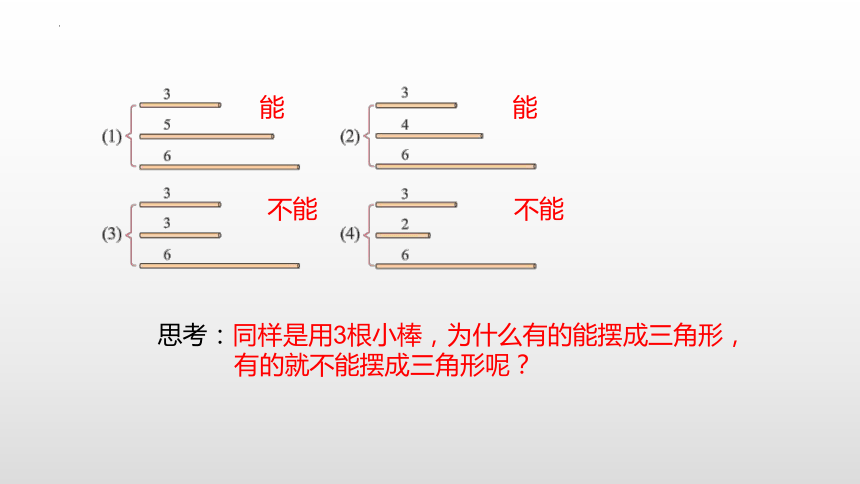
能
能
不能
不能
思考:同样是用3根小棒,为什么有的能摆成三角形,
有的就不能摆成三角形呢?
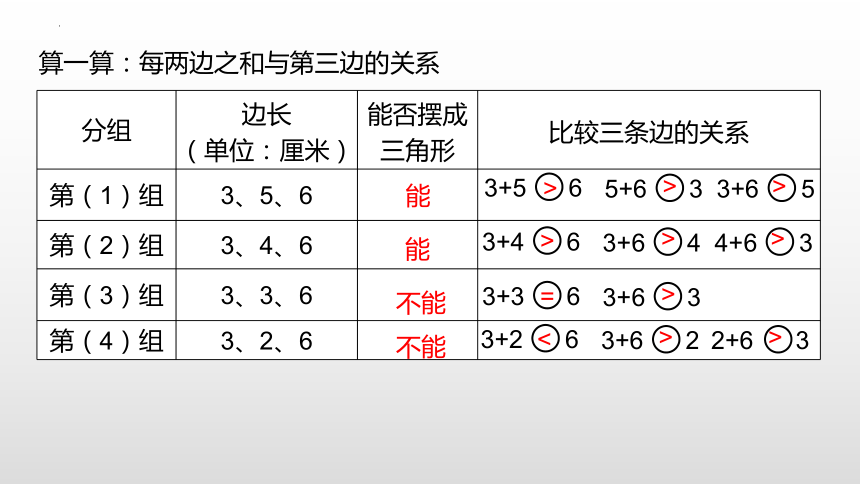
算一算:每两边之和与第三边的关系
分组 边长 (单位:厘米) 能否摆成三角形 比较三条边的关系
第(1)组 3、5、6
第(2)组 3、4、6
第(3)组 3、3、6
第(4)组 3、2、6
能
能
不能
不能
3+5 6
3+6 5
5+6 3
3+4 6
4+6 3
3+6 4
3+3 6
3+6 3
3+2 6
2+6 3
3+6 2
>
>
>
>
>
>
=
>
<
>
>
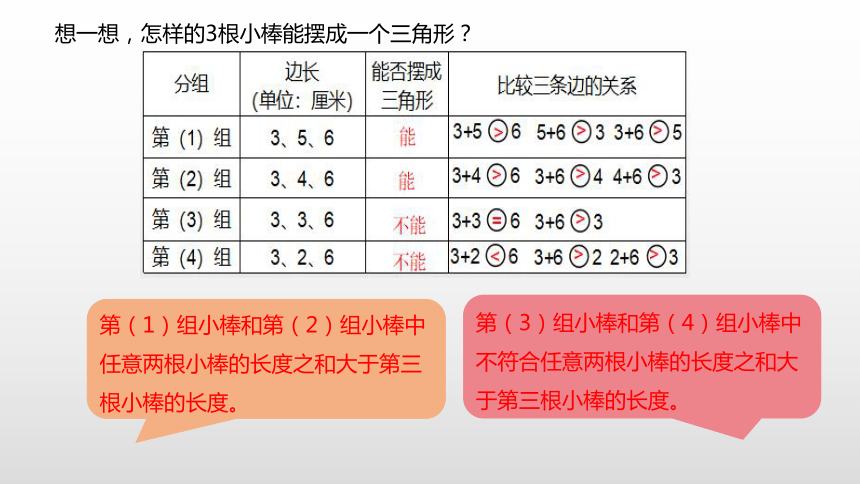
想一想,怎样的3根小棒能摆成一个三角形?
第(1)组小棒和第(2)组小棒中任意两根小棒的长度之和大于第三根小棒的长度。
第(3)组小棒和第(4)组小棒中不符合任意两根小棒的长度之和大于第三根小棒的长度。
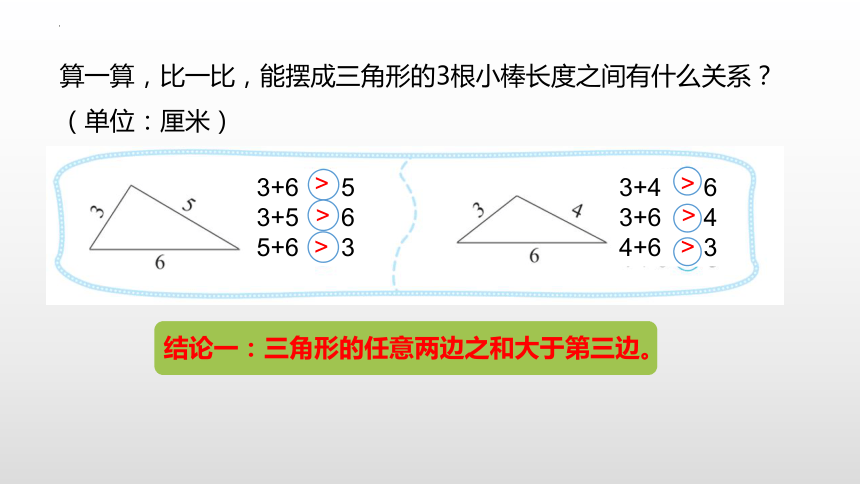
算一算,比一比,能摆成三角形的3根小棒长度之间有什么关系?(单位:厘米)
3+6 5
3+5 6
5+6 3
3+4 6
3+6 4
4+6 3
结论一:三角形的任意两边之和大于第三边。
>
>
>
>
>
>
(1)
6
7
9
( )
在能拼成三角形的各组小棒下面画“√”,不能拼成的下面画“×”(单位:cm)。
√
(2)
13
6
7
( )
×
6+7>9
6+9>7
7+9>6
13+6>7
13+7>6
6+7=13
算一算,判断下列各组中的三条线段能否围成三角形(单位:cm)。
(1) 7 3 4 ( ) (2) 3 9 7 ( )
(3) 12 9 11 ( ) (4) 6 4 11 ( )
(5) 48 32 54 ( ) (6) 13 18 30 ( )
否
三角形的任意两条边之和大于第三边。
是
是
否
是
是
练一练:
(1)当一个三角形的两条边分别长3厘米、7厘米时,第三条边长度可能是( )
A.2厘米 B.3厘米 C.5厘米
(2)下面各组的三条线段,能组成三角形的是( )。
A.3cm,4cm,6cm B.2cm,5cm,3cm C.1cm,3cm,5cm
C
选一选。
A
练一练:
下面是四个三角形中的三边长度,通过计算发现规律。
分组 边长 (单位:厘米) 比较三条边的关系
三角形(1) 3、5、6
三角形(2) 3、4、6
三角形(3) 3、5、7
三角形(4) 3、2、4
3+5 6
3+4 6
3+5 7
2+3 4
>
>
>
>
结论二:较短的两边之和大于较长边,这三条边一定能围成三角形 。
在能摆成三角形的小棒下面画“√”。(列算式判断)
3+4>6
1+2=3
5+7>11
√
×
√
练一练:
(3) 以长为3cm、5cm、7cm的三条线段为边,可构成一个三角形。( )
(1)任何三条线段都能组成一个三角形。 ( )
(2)因为a+b>c,所以a、b、c三边可以构成三角形。 ( )
×
×
判一判。(对的画“√”,错的画“×”)
√
用同样长的小棒摆一摆,完成下表。
(1)3根小棒能否摆成一个三角形?它是什么三角形?
(2)4根小棒能否摆成一个三角形?5根、6根呢?
小棒根数 3 4 5 6
能摆成三角形吗
是什么三角形
能
等边
不能
能
等腰
能
等边
算一算,比一比,能摆成三角形的3根小棒长度之间有什么关系?(单位:厘米)
6-3 5
6-5 3
5-3 6
6-3 4
6-4 3
4-3 6
结论三:三角形的任意两边之差小于第三边。
<
<
<
<
<
<
木工师傅要用木条做一个三角形,其中一条边的长15是分米,另一条边的长是9分米。那么第三条边的长可能是哪些长度?(木条长度为整分米数)
第三条边的长
15-9<
<15+9
6<第三条边的长<24
答:第三条边可以是7--23分米。
三角形的任意两条边的和大于第三边;任意两边的差小于第三边。
第三条边的长度最短是7分米,最长是23分米。
爸爸要用木条做一个三角形框架,其中一条边的长30是厘米,另一条边的长是18厘米。让小明帮他找一根木条,小明找的木条的长可能是多少厘米?(木条长度为整厘米数)
第三条边的长
30-18<
<30+18
12<第三条边的长<48
答:小明找的木条的长可能是13--47厘米。
三角形的任意两条边的和大于第三边,任意两边的差小于第三边。
练一练:
第三条边的长度最短是13厘米,最长是47厘米。
结论一:三角形任意两边之和大于第三边。
结论二:较短的两边之和大于较长边,这三条边一定能组成三角形 。
结论三:三角形的任意两边之差小于第三边。
①
取3根都是3cm的小棒。
等边三角形
②
取2根3cm、1根4cm的小棒。
等腰三角形
③
取3cm、4cm、6cm的小棒各1根。
钝角三角形
3
3
3
4
3
3
6
3
4
3
4
6
从下面5根小棒中任意取出3根,摆出三种不同的的三角形。(单位:厘米)
3
3
( 5, 5, 5 )
5
7
10
从下面5根小棒中任意取出3根,可以摆出多少种不同的的三角形?一一列举出来。(单位:厘米)
5
5
( 5, 5, 7 )
( 5, 7, 10 )
等边三角形
等腰三角形
钝角三角形
练一练:
一个等腰三角形的周长是30厘米,一边长为12厘米,求其他两边的长。
如果用12厘米长的边做腰:
30-12-12=6(cm)
如果用12厘米长的边做底:
(30-12)÷2=9(cm)
答:其他两边的长可能是12厘米和6厘米,或12厘米和9厘米。
一个等腰三角形的周长是46厘米,一边长为20厘米,求其他两边的长。
如果用20厘米长的边做腰:
46-20-20=6(cm)
如果用20厘米长的边做底:
(46-20)÷2=8(cm)
答:其他两边的长可能是20厘米和6厘米,或20厘米和8厘米。
练一练:
一个等腰三角形的周长是48厘米,一边长为16厘米,求其他两边的长。
如果用16厘米长的边做腰:
48-16-16=16(cm)
这是一个等边三角形。
答:三条边的长都是16厘米。
练一练:
用一根12厘米的绳子围成一个三角形,如果边长取整厘米数(转角处忽略不计),有多少种围法?写出每种围法的三条边的长度。
12 cm
( 1、 1、 10 )
( 1、 2、 9 )
( 1、 3、 8 )
( 1、 4、 7 )
( 2、 2、 8 )
( 2、 3、 7 )
( 2、 4、 6 )
×
×
×
×
×
×
×
( 1、 5、6 )
×
( 2、 5、 5 )
( 3、 3、 6 )
( 3、 4、 5 )
( 4、 4、 4 )
√
×
√
√
用一根10厘米的绳子围成一个三角形,如果边长取整厘米数(转角处忽略不计),有多少种围法?写出每种围法的三条边的长度。
10 cm
( 1、 1、 8 )
( 1、 2、 7 )
( 1、 3、 6 )
( 1、 4、 5 )
( 2、 3、 5 )
( 2、 4、 4 )
( 3、 3、 4 )
×
×
×
×
×
√
√
( 2、 2、 6 )
×
练一练:
摆1个三角形要3根小棒,
摆2个三角形要5根小棒,
摆3个三角形要( )根小棒,
摆4个三角形要( )根小棒。
用小棒照样子摆一摆。
7
9
你发现了什么?
三角形个数
小棒数量
规律
3
2×1+1
5
2×2+1
2×3+1
2×4+1
7
9
……
……
……
n个三角形
2n+1
2n+1
摆18个三角形要多少根小棒?
用75根小棒能摆多少个三角形?
用小棒照样子摆一摆。
2×18+1=37(根)
(75-1)÷2=37(个)
摆100个三角形要多少根小棒?
用61根小棒能摆多少个三角形?
用小棒照样子摆一摆。
2×100+1=201(根)
(61-1)÷2=33(个)
练一练:
谢谢观看!
如果三角形的两条边的长度分别是7cm和12cm,那么第三条边可能是多少厘米?
因为7+12=19(cm),所以第三条边应当小于19cm。
因为12-7=5(cm),所以第三条边应当大于5cm。
答:第三条边可能是10cm。
(答案不唯一)
三角形的任意两条边的和大于第三边,任意两边的差小于第三边。
如果三角形的两条边的长分别是5厘米和8厘米,那么第三条边的长可能是几厘米?写出两种答案。
第三条边的长
8-5<
<8+5
3<第三条边的长<13
答:第三条边可能是4厘米、5厘米。
(答案不唯一)
三角形的任意两条边的和大于第三边,任意两边的差小于第三边。
1、填一填。
(1)一个三角形的内角和是( ),把三角形的每条边都扩大到原来的5倍后,这个三角形的内角和是( )。
(2)两个相同的小三角形拼成一个大三角形,这个大三角形的内角和是( )。
180°
180°
180°
2、已知一个等腰三角形的底角是72度,顶角是多少度?
180°-72°-72 = 36°
3、已知一个等腰三角形的顶角度数是底角度数的2倍,那么顶角和底角分别是多少度?这是一个什么类型的三角形?
180°÷(1+1+2) = 45°
45°×2 = 90°
答:顶角是90°,底角是45°。它是一个等腰直角三角形。
答:顶角是36°。
复习:
认识三角形和四边形
三角形边的关系
北师大版 数学 四年级 下册
给你3根小棒,你能用它们围一个三角形吗?
只要给你3根小棒,你就能用它们围一个三角形吗?
用小棒摆三角形,上面哪组能摆成呢?
算一算:每两边之和与第三边的关系
3cm
5cm
6cm
(1)
5cm
3cm
5cm
3cm
5cm
3cm
6cm
第(1)组小棒能摆成三角形。
算一算:每两边之和与第三边的关系
3cm
4cm
6cm
(2)
4cm
3cm
4cm
3cm
4cm
3cm
4cm
3cm
6cm
第(2)组能摆成三角形。
算一算:每两边之和与第三边的关系
3cm
3cm
6cm
(3)
6cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
3cm
第(3)组不能摆成三角形。
算一算:每两边之和与第三边的关系
3cm
2cm
6cm
(4)
6cm
3cm
2cm
3cm
2cm
3cm
2cm
3cm
2cm
3cm
2cm
第(4)组不能摆成三角形。
能
能
不能
不能
思考:同样是用3根小棒,为什么有的能摆成三角形,
有的就不能摆成三角形呢?
算一算:每两边之和与第三边的关系
分组 边长 (单位:厘米) 能否摆成三角形 比较三条边的关系
第(1)组 3、5、6
第(2)组 3、4、6
第(3)组 3、3、6
第(4)组 3、2、6
能
能
不能
不能
3+5 6
3+6 5
5+6 3
3+4 6
4+6 3
3+6 4
3+3 6
3+6 3
3+2 6
2+6 3
3+6 2
>
>
>
>
>
>
=
>
<
>
>
想一想,怎样的3根小棒能摆成一个三角形?
第(1)组小棒和第(2)组小棒中任意两根小棒的长度之和大于第三根小棒的长度。
第(3)组小棒和第(4)组小棒中不符合任意两根小棒的长度之和大于第三根小棒的长度。
算一算,比一比,能摆成三角形的3根小棒长度之间有什么关系?(单位:厘米)
3+6 5
3+5 6
5+6 3
3+4 6
3+6 4
4+6 3
结论一:三角形的任意两边之和大于第三边。
>
>
>
>
>
>
(1)
6
7
9
( )
在能拼成三角形的各组小棒下面画“√”,不能拼成的下面画“×”(单位:cm)。
√
(2)
13
6
7
( )
×
6+7>9
6+9>7
7+9>6
13+6>7
13+7>6
6+7=13
算一算,判断下列各组中的三条线段能否围成三角形(单位:cm)。
(1) 7 3 4 ( ) (2) 3 9 7 ( )
(3) 12 9 11 ( ) (4) 6 4 11 ( )
(5) 48 32 54 ( ) (6) 13 18 30 ( )
否
三角形的任意两条边之和大于第三边。
是
是
否
是
是
练一练:
(1)当一个三角形的两条边分别长3厘米、7厘米时,第三条边长度可能是( )
A.2厘米 B.3厘米 C.5厘米
(2)下面各组的三条线段,能组成三角形的是( )。
A.3cm,4cm,6cm B.2cm,5cm,3cm C.1cm,3cm,5cm
C
选一选。
A
练一练:
下面是四个三角形中的三边长度,通过计算发现规律。
分组 边长 (单位:厘米) 比较三条边的关系
三角形(1) 3、5、6
三角形(2) 3、4、6
三角形(3) 3、5、7
三角形(4) 3、2、4
3+5 6
3+4 6
3+5 7
2+3 4
>
>
>
>
结论二:较短的两边之和大于较长边,这三条边一定能围成三角形 。
在能摆成三角形的小棒下面画“√”。(列算式判断)
3+4>6
1+2=3
5+7>11
√
×
√
练一练:
(3) 以长为3cm、5cm、7cm的三条线段为边,可构成一个三角形。( )
(1)任何三条线段都能组成一个三角形。 ( )
(2)因为a+b>c,所以a、b、c三边可以构成三角形。 ( )
×
×
判一判。(对的画“√”,错的画“×”)
√
用同样长的小棒摆一摆,完成下表。
(1)3根小棒能否摆成一个三角形?它是什么三角形?
(2)4根小棒能否摆成一个三角形?5根、6根呢?
小棒根数 3 4 5 6
能摆成三角形吗
是什么三角形
能
等边
不能
能
等腰
能
等边
算一算,比一比,能摆成三角形的3根小棒长度之间有什么关系?(单位:厘米)
6-3 5
6-5 3
5-3 6
6-3 4
6-4 3
4-3 6
结论三:三角形的任意两边之差小于第三边。
<
<
<
<
<
<
木工师傅要用木条做一个三角形,其中一条边的长15是分米,另一条边的长是9分米。那么第三条边的长可能是哪些长度?(木条长度为整分米数)
第三条边的长
15-9<
<15+9
6<第三条边的长<24
答:第三条边可以是7--23分米。
三角形的任意两条边的和大于第三边;任意两边的差小于第三边。
第三条边的长度最短是7分米,最长是23分米。
爸爸要用木条做一个三角形框架,其中一条边的长30是厘米,另一条边的长是18厘米。让小明帮他找一根木条,小明找的木条的长可能是多少厘米?(木条长度为整厘米数)
第三条边的长
30-18<
<30+18
12<第三条边的长<48
答:小明找的木条的长可能是13--47厘米。
三角形的任意两条边的和大于第三边,任意两边的差小于第三边。
练一练:
第三条边的长度最短是13厘米,最长是47厘米。
结论一:三角形任意两边之和大于第三边。
结论二:较短的两边之和大于较长边,这三条边一定能组成三角形 。
结论三:三角形的任意两边之差小于第三边。
①
取3根都是3cm的小棒。
等边三角形
②
取2根3cm、1根4cm的小棒。
等腰三角形
③
取3cm、4cm、6cm的小棒各1根。
钝角三角形
3
3
3
4
3
3
6
3
4
3
4
6
从下面5根小棒中任意取出3根,摆出三种不同的的三角形。(单位:厘米)
3
3
( 5, 5, 5 )
5
7
10
从下面5根小棒中任意取出3根,可以摆出多少种不同的的三角形?一一列举出来。(单位:厘米)
5
5
( 5, 5, 7 )
( 5, 7, 10 )
等边三角形
等腰三角形
钝角三角形
练一练:
一个等腰三角形的周长是30厘米,一边长为12厘米,求其他两边的长。
如果用12厘米长的边做腰:
30-12-12=6(cm)
如果用12厘米长的边做底:
(30-12)÷2=9(cm)
答:其他两边的长可能是12厘米和6厘米,或12厘米和9厘米。
一个等腰三角形的周长是46厘米,一边长为20厘米,求其他两边的长。
如果用20厘米长的边做腰:
46-20-20=6(cm)
如果用20厘米长的边做底:
(46-20)÷2=8(cm)
答:其他两边的长可能是20厘米和6厘米,或20厘米和8厘米。
练一练:
一个等腰三角形的周长是48厘米,一边长为16厘米,求其他两边的长。
如果用16厘米长的边做腰:
48-16-16=16(cm)
这是一个等边三角形。
答:三条边的长都是16厘米。
练一练:
用一根12厘米的绳子围成一个三角形,如果边长取整厘米数(转角处忽略不计),有多少种围法?写出每种围法的三条边的长度。
12 cm
( 1、 1、 10 )
( 1、 2、 9 )
( 1、 3、 8 )
( 1、 4、 7 )
( 2、 2、 8 )
( 2、 3、 7 )
( 2、 4、 6 )
×
×
×
×
×
×
×
( 1、 5、6 )
×
( 2、 5、 5 )
( 3、 3、 6 )
( 3、 4、 5 )
( 4、 4、 4 )
√
×
√
√
用一根10厘米的绳子围成一个三角形,如果边长取整厘米数(转角处忽略不计),有多少种围法?写出每种围法的三条边的长度。
10 cm
( 1、 1、 8 )
( 1、 2、 7 )
( 1、 3、 6 )
( 1、 4、 5 )
( 2、 3、 5 )
( 2、 4、 4 )
( 3、 3、 4 )
×
×
×
×
×
√
√
( 2、 2、 6 )
×
练一练:
摆1个三角形要3根小棒,
摆2个三角形要5根小棒,
摆3个三角形要( )根小棒,
摆4个三角形要( )根小棒。
用小棒照样子摆一摆。
7
9
你发现了什么?
三角形个数
小棒数量
规律
3
2×1+1
5
2×2+1
2×3+1
2×4+1
7
9
……
……
……
n个三角形
2n+1
2n+1
摆18个三角形要多少根小棒?
用75根小棒能摆多少个三角形?
用小棒照样子摆一摆。
2×18+1=37(根)
(75-1)÷2=37(个)
摆100个三角形要多少根小棒?
用61根小棒能摆多少个三角形?
用小棒照样子摆一摆。
2×100+1=201(根)
(61-1)÷2=33(个)
练一练:
谢谢观看!
如果三角形的两条边的长度分别是7cm和12cm,那么第三条边可能是多少厘米?
因为7+12=19(cm),所以第三条边应当小于19cm。
因为12-7=5(cm),所以第三条边应当大于5cm。
答:第三条边可能是10cm。
(答案不唯一)
三角形的任意两条边的和大于第三边,任意两边的差小于第三边。
如果三角形的两条边的长分别是5厘米和8厘米,那么第三条边的长可能是几厘米?写出两种答案。
第三条边的长
8-5<
<8+5
3<第三条边的长<13
答:第三条边可能是4厘米、5厘米。
(答案不唯一)
三角形的任意两条边的和大于第三边,任意两边的差小于第三边。
