《平移》说课课件
图片预览








文档简介
课件24张PPT。说课题目 平移农垦实验中学 钱 丽一.教材分析二.教法与学法分析 三.教学过程分析 《平移》是人教版《数学》七年级下册第五章第四节的内容,是学生认识的第一种图形全等变换。之前,在小学五年级学生学习平行四边形面积公式的推导过程中就对平移有过最初印象。在这一章里,学生种学习了平行线的判定和性质后,才真正的了解平移的特征。接下来,在第六章里,教材还安排了“用坐标表示平移”,通过学习,学生对平移的方向和距离会有进 一步的认识。 因此,教材对这个问题的处理是分为三个阶段呈螺旋上升、层层递进。学好它既是对平行的后续认识,同时也是今后学习其它两种全等变换的基础。???一. 教材分析1、知识技能:
(1)能发现、归纳图形平移的特征
(2)根据平移的特征,会作简单的图形平移。
2、过程与方法
通过学生经历探索图形平移基本特征的过程,发展学生抽象概括能力;增强学生应用所学知识解决实际问题的能力。
3、情感态度:
学生亲历观察、操作、想象、交流、归纳等活动,体验数学充满探索和创造,从而激发学生的学习热情。???一. 教材分析教学重点:平移的特征和作图方法。
教学难点:作图形的平移。教学目标
该年龄段的学生学习积极性高,探索欲望强烈,但数学活动的经验较少,探索效率较低,合作交流能力有待加强.二.教法与学法分析学情分析 1.教法: 根据本节课的教学目标、教材内容以及学生的认知特点,我采用启发式、探索式的教学方法,意在帮助学生通过观察,自己动手,从实践中获得知识。整个探究学习的过程充满了师生之间、学生之间的交流与互动,体现了教师是教学活动的组织者、引导者,而学生才是学习的主体。二. 教法与学法分析 2.学法 利用学生的好奇心设疑,解疑,组织活泼互动、有效的教学活动,鼓励学生积极参与,大胆猜想,使学生在自主探索与合作交流中理解和掌握本节课的内容。三 教 学 过 程教学过程 创设情境
探究新知
运用新知
归纳总结
布置作业三、 教 学 过 程一、创设情境
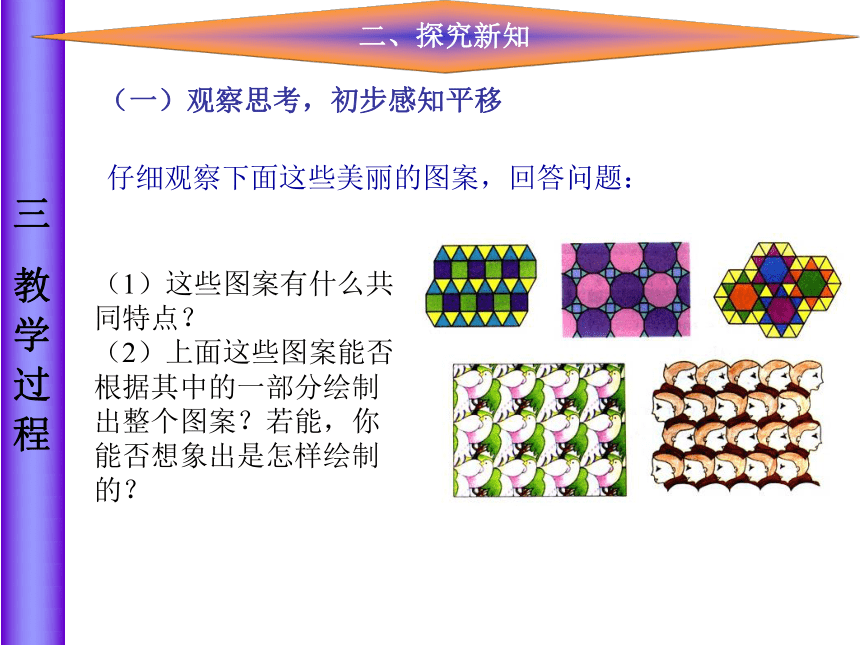
如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是0.5m)。请你猜想草地的面积是多少。猜猜看三 教 学 过 程二、探究新知仔细观察下面这些美丽的图案,回答问题:(1)这些图案有什么共同特点?
(2)上面这些图案能否根据其中的一部分绘制出整个图案?若能,你能否想象出是怎样绘制的?观察思考,初步感知(一)观察思考,初步感知平移三 教 学 过 程二、探究新知想一想
如何在一张半透明的纸上,画出一排形状和大小如图的雪人?
(二)动手操作,探索平移特征作品它们的形状、大小完全相等。三 教 学 过 程二、探究新知做一做
在所画出的相邻两个雪人中,找出三组对应点,连结这些对应点,观察得出的线段,它们的位置、长短有什么关系?它们平行且相等归纳与总结 1、把一个图形整体沿某一直线方向移动,会得到一个新的图形.新图形与原图形的形状和大小完全相同.
2、新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点就是对应点。连接各组对应点的线段平行且相等
3、图形的这种移动,叫做平移变换,简称平移。三 教 学 过 程二、探究新知注意
图形的平移不一定是水平的,也不一定是竖直的。
三 教 学 过 程三、运用新知2.下图中的变换属于平移的有哪些?1.试举例说说生活中的平移现象。三 教 学 过 程三、运用新知例:经过平移,三角形ABC的顶点A移到了点E,作出平移后的三角形EDF.3.学习例题ADFEBC问题1:要画出平移后的三角形,关键是什么?
(找到三角形的三个顶点)问题2:怎样找到这些点?你的根据是什么?三 教 学 过 程三、运用新知4.答疑
如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是0.5m)。请你猜想草地的面积是多少。你知道如何解答了吗?(20 – 0.5) ×8=156m2三 教 学 过 程三、应用新知实例图形作图解题感受平移现象直观感知平移特征体会平移特征体会学有价值的数学三 教 学 过 程四、归纳总结1、这节课我们一起学习了哪些知识?
2、对这些知识你有什么体会,请和大家交流. 三 教 学 过 程五、布置作业 P31习题5.4 第5题 今日作业5.用平移方法怎样得出平行四边形面积公式
S = ah四 板书设计四、板书设计 课题
平移的特征
例 题
投影区
五.板书设计:三 教 学 过 程设计说明这整个教学环节是遵从“循序渐进”的教学原则来设计的。首先结合身边熟悉的实例感受平移现象,然后,把它抽象成数学图形让学生直观感知平移特征,渗透数学建模思想;接着动手操作,体会平移特征;最后用平移特征解决实际问题,体会数学知识的价值。
(1)能发现、归纳图形平移的特征
(2)根据平移的特征,会作简单的图形平移。
2、过程与方法
通过学生经历探索图形平移基本特征的过程,发展学生抽象概括能力;增强学生应用所学知识解决实际问题的能力。
3、情感态度:
学生亲历观察、操作、想象、交流、归纳等活动,体验数学充满探索和创造,从而激发学生的学习热情。???一. 教材分析教学重点:平移的特征和作图方法。
教学难点:作图形的平移。教学目标
该年龄段的学生学习积极性高,探索欲望强烈,但数学活动的经验较少,探索效率较低,合作交流能力有待加强.二.教法与学法分析学情分析 1.教法: 根据本节课的教学目标、教材内容以及学生的认知特点,我采用启发式、探索式的教学方法,意在帮助学生通过观察,自己动手,从实践中获得知识。整个探究学习的过程充满了师生之间、学生之间的交流与互动,体现了教师是教学活动的组织者、引导者,而学生才是学习的主体。二. 教法与学法分析 2.学法 利用学生的好奇心设疑,解疑,组织活泼互动、有效的教学活动,鼓励学生积极参与,大胆猜想,使学生在自主探索与合作交流中理解和掌握本节课的内容。三 教 学 过 程教学过程 创设情境
探究新知
运用新知
归纳总结
布置作业三、 教 学 过 程一、创设情境
如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是0.5m)。请你猜想草地的面积是多少。猜猜看三 教 学 过 程二、探究新知仔细观察下面这些美丽的图案,回答问题:(1)这些图案有什么共同特点?
(2)上面这些图案能否根据其中的一部分绘制出整个图案?若能,你能否想象出是怎样绘制的?观察思考,初步感知(一)观察思考,初步感知平移三 教 学 过 程二、探究新知想一想
如何在一张半透明的纸上,画出一排形状和大小如图的雪人?
(二)动手操作,探索平移特征作品它们的形状、大小完全相等。三 教 学 过 程二、探究新知做一做
在所画出的相邻两个雪人中,找出三组对应点,连结这些对应点,观察得出的线段,它们的位置、长短有什么关系?它们平行且相等归纳与总结 1、把一个图形整体沿某一直线方向移动,会得到一个新的图形.新图形与原图形的形状和大小完全相同.
2、新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点就是对应点。连接各组对应点的线段平行且相等
3、图形的这种移动,叫做平移变换,简称平移。三 教 学 过 程二、探究新知注意
图形的平移不一定是水平的,也不一定是竖直的。
三 教 学 过 程三、运用新知2.下图中的变换属于平移的有哪些?1.试举例说说生活中的平移现象。三 教 学 过 程三、运用新知例:经过平移,三角形ABC的顶点A移到了点E,作出平移后的三角形EDF.3.学习例题ADFEBC问题1:要画出平移后的三角形,关键是什么?
(找到三角形的三个顶点)问题2:怎样找到这些点?你的根据是什么?三 教 学 过 程三、运用新知4.答疑
如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是0.5m)。请你猜想草地的面积是多少。你知道如何解答了吗?(20 – 0.5) ×8=156m2三 教 学 过 程三、应用新知实例图形作图解题感受平移现象直观感知平移特征体会平移特征体会学有价值的数学三 教 学 过 程四、归纳总结1、这节课我们一起学习了哪些知识?
2、对这些知识你有什么体会,请和大家交流. 三 教 学 过 程五、布置作业 P31习题5.4 第5题 今日作业5.用平移方法怎样得出平行四边形面积公式
S = ah四 板书设计四、板书设计 课题
平移的特征
例 题
投影区
五.板书设计:三 教 学 过 程设计说明这整个教学环节是遵从“循序渐进”的教学原则来设计的。首先结合身边熟悉的实例感受平移现象,然后,把它抽象成数学图形让学生直观感知平移特征,渗透数学建模思想;接着动手操作,体会平移特征;最后用平移特征解决实际问题,体会数学知识的价值。
