第六章 圆周运动 专题强化7 水平面内的圆周运动的临界问题 巩固练(含解析)—2023-2024学年高中物理人教版必修二
文档属性
| 名称 | 第六章 圆周运动 专题强化7 水平面内的圆周运动的临界问题 巩固练(含解析)—2023-2024学年高中物理人教版必修二 |

|
|
| 格式 | docx | ||
| 文件大小 | 332.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览




文档简介
专题强化7 水平面内的圆周运动的临界问题
1.(2023·南通市高一期末)一个杯子放在水平餐桌转盘上随转盘做匀速圆周运动,角速度恒定,则( )
A.杯子受重力、支持力、摩擦力和向心力作用
B.杯子受到的摩擦力方向始终指向转盘中心
C.杯子离转盘中心越近越容易做离心运动
D.若给杯子中加水,杯子更容易做离心运动
2.如图所示,粗糙水平圆盘上,质量相等的A、B两物块叠放在一起,随圆盘一起做匀速圆周运动,则下列说法正确的是( )
A.A、B都有沿切线方向且向后滑动的趋势
B.B运动所需的向心力大于A运动所需的向心力
C.盘对B的摩擦力是B对A的摩擦力的2倍
D.若B相对圆盘先滑动,则A、B间的动摩擦因数μA小于盘与B间的动摩擦因数μB
3.某同学用硬塑料管和铁质螺丝帽研究匀速圆周运动。如图所示,该同学将螺丝帽套在塑料管上,手握塑料管使其保持竖直并在水平面内做半径为r的匀速圆周运动。假设螺丝帽与塑料管间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,重力加速度为g。下列分析正确的是( )
A.若塑料管转动速度增大,螺丝帽受到的摩擦力越大
B.当螺丝帽恰好不下滑时,手转动塑料管的角速度ω=
C.若塑料管的转动速度持续增大,螺丝帽最终会沿塑料管上滑
D.若塑料管的转动速度持续增大,地面对人的支持力始终不变
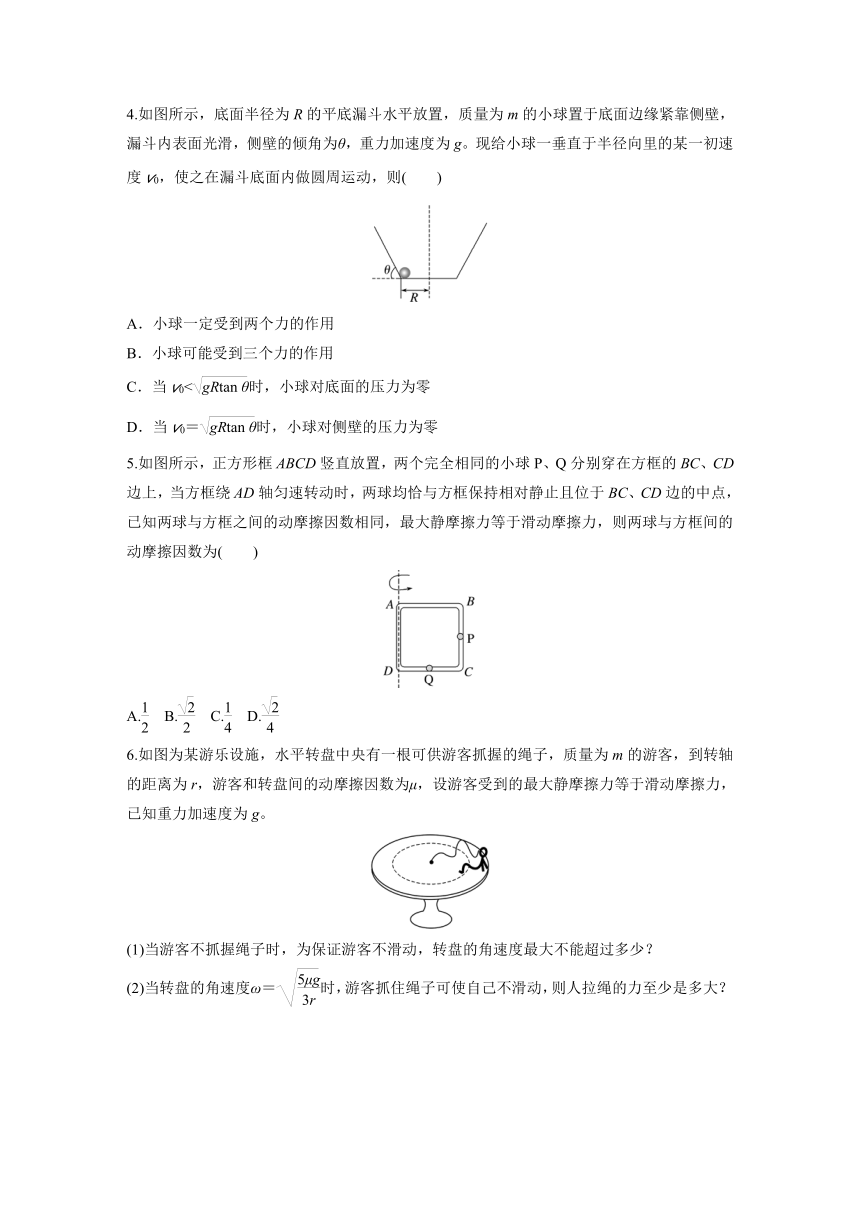
4.如图所示,底面半径为R的平底漏斗水平放置,质量为m的小球置于底面边缘紧靠侧壁,漏斗内表面光滑,侧壁的倾角为θ,重力加速度为g。现给小球一垂直于半径向里的某一初速度v0,使之在漏斗底面内做圆周运动,则( )
A.小球一定受到两个力的作用
B.小球可能受到三个力的作用
C.当v0<时,小球对底面的压力为零
D.当v0=时,小球对侧壁的压力为零
5.如图所示,正方形框ABCD竖直放置,两个完全相同的小球P、Q分别穿在方框的BC、CD边上,当方框绕AD轴匀速转动时,两球均恰与方框保持相对静止且位于BC、CD边的中点,已知两球与方框之间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力,则两球与方框间的动摩擦因数为( )
A. B. C. D.
6.如图为某游乐设施,水平转盘中央有一根可供游客抓握的绳子,质量为m的游客,到转轴的距离为r,游客和转盘间的动摩擦因数为μ,设游客受到的最大静摩擦力等于滑动摩擦力,已知重力加速度为g。
(1)当游客不抓握绳子时,为保证游客不滑动,转盘的角速度最大不能超过多少?
(2)当转盘的角速度ω=时,游客抓住绳子可使自己不滑动,则人拉绳的力至少是多大?
7.如图所示,在匀速转动的水平圆盘上,沿半径方向放着用水平细线相连的质量相等的两个物体A和B,它们分居圆心两侧,质量均为m,与圆心距离分别为RA=r,RB=2r,与盘间的动摩擦因数μ相同,重力加速度为g,设最大静摩擦力等于滑动摩擦力。当圆盘转速加快到两物体刚好还未发生滑动时,下列说法正确的是( )
A.此时绳子张力为FT=4μmg
B.此时圆盘的角速度为ω=
C.此时A所受摩擦力方向沿半径指向圆内
D.若此时烧断绳子,A仍相对盘静止,B将做离心运动
8.如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴转动的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合。转台以一定角速度匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后小物块随陶罐一起转动且相对罐壁静止,此时小物块受到的摩擦力恰好为0,且它和O点的连线与OO′之间的夹角θ为60°,重力加速度为g。求转台转动的角速度。
9.(2022·南通市高一期末)如图所示,水平转盘上放有质量为m的物块,物块到转轴的距离为r。一段绳的一端与物块相连,另一端系在圆盘中心上方r处,绳恰好伸直,物块和转盘间的动摩擦因数为μ,设物块受到的最大静摩擦力等于滑动摩擦力,已知重力加速度为g。
(1)当水平转盘以角速度ω1匀速转动时,绳上恰好有张力,求ω1的值;
(2)当水平转盘以角速度ω2匀速转动时,物块恰好离开转盘,求ω2的值。
10.(2023·南通市高一统考期末)如图所示,一质量为m的小球用长度均为L的两轻绳a、b连接,绳a的另一端固定在竖直细杆的P点,绳b的另一端固定在杆上距P点为L的Q点。当杆绕其竖直中心轴匀速转动时,将带动小球在水平面内做匀速圆周运动。不计空气阻力,重力加速度为g。
(1)当绳b刚好拉直(无弹力)时,求小球的线速度大小v;
(2)若两绳能承受的最大拉力均为4mg,求小球绕杆做圆周运动的最小周期T。
11.(2023·苏州市高一统考期中)如图甲所示,一半径为R=0.5 m的水平转盘可以绕着竖直轴OO′转动,水平转盘中心O处有一个光滑小孔,用一根长为L=1 m的细线穿过小孔将质量分别为mA=0.2 kg、mB=0.5 kg的小球A和小物块B连接。现让小球和水平转盘各以一定的角速度在水平面内转动起来,小物块B与水平转盘间的动摩擦因数μ=0.3,且始终处于水平转盘的边缘处与转盘相对静止,取g=10 m/s2,求:
(1)若小球A的角速度ω=5 rad/s,细线与竖直方向的夹角θ;
(2)在满足(1)中的条件下,通过计算给出水平转盘角速度ωB的取值范围,并在图乙中画出Ff-ω2图像(假设最大静摩擦力等于滑动摩擦力,且规定沿半径指向圆心为正方向)。
(可能使用到的数据:sin 30°=,cos 30°=,sin 37°=,cos 37°=)
专题强化练7 水平面内的圆周运动的临界问题
1.B [杯子受到重力、支持力和摩擦力三个力,向心力不是物体的实际受力,故A错误;杯子做匀速圆周运动,向心力由摩擦力提供,始终指向转盘中心,故B正确;杯子做匀速圆周运动Fn=Ff=mω2r,离转盘中心越近,所需摩擦力越小,越不容易达到最大静摩擦力,越不容易做离心运动,故C错误;根据Ff=mω2r≤μmg可知,给杯子中加水,杯子不会更容易做离心运动,故D错误。]
2.C [把A、B当成一个整体,在水平方向上只受摩擦力作用,所以,摩擦力即物块所受合外力,提供向心力,摩擦力方向指向圆心,物块有沿径向向外滑动的趋势,故A错误;物块做匀速圆周运动,向心力F=m,A、B质量相同,一起做匀速圆周运动的角速度、半径也相等,所以,两者运动所需的向心力相等,故B错误;由受力分析可知B对A的摩擦力等于F,盘对B的摩擦力等于2F,故C正确;若B相对圆盘先滑动,则2μBmg-μAmg<μAmg,即μB<μA,故D错误。]
3.D [若塑料管转动速度增大,螺丝帽受到的摩擦力不变,等于重力,螺丝帽不会沿塑料管上滑,A、C错误;对螺丝帽根据牛顿第二定律得FN=mω2r,根据平衡条件得μFN=mg,解得ω=,B错误。因系统无竖直方向加速度,无论转速多大,地面对人的支持力等于系统总重力,D正确。]
4.B [对小球,由牛顿第二定律,有
FN2sin θ=m
FN1+FN2cos θ=mg
可知侧壁对小球的支持力FN2不可能为零,底面对小球的支持力FN1可能为零。所以小球可能受到三个力的作用,也可能受到两个力的作用。由牛顿第三定律可知,小球对侧壁的压力不可能为零,所以A、D错误,B正确;当v0<时,FN1=mg->0,由牛顿第三定律可知,当v0<时,小球对底面的压力不为零,故C错误。]
5.B [设方框边长为l,小球质量为m,对P球,根据牛顿第二定律可得μmω2l=mg,对Q球,根据牛顿第二定律可得μmg=mω2,联立解得μ=,故选B。]
6.(1) (2)μmg
解析 (1)当游客受到的摩擦力达到最大静摩擦力时恰好不滑动
μmg=mω02r
得ω0=
(2)由题意有FT+μmg=mω2r
得FT=μmg
由牛顿第三定律得:
FT′=FT=μmg。
7.B [A和B随着圆盘转动时,合外力提供向心力,则F=mω2R,B的运动半径比A的半径大,所以B所需向心力大,细线拉力相等,所以当圆盘转速加快到两物体刚好还未发生滑动时,B的静摩擦力方向沿半径指向圆心,A的最大静摩擦力方向沿半径指向圆外,对物体A、B,根据牛顿第二定律分别得:FT-μmg=mω2r,FT+μmg=mω2·2r,解得:FT=3μmg,ω=,此时A所需的向心力大小为FnA=mω2r=2μmg,B所需的向心力大小为FnB=mω2·2r=4μmg,若此时烧断细线,A、B的最大静摩擦力均不足以提供物体所需向心力,则A、B均做离心运动,故B正确,A、C、D错误。]
8.
解析 对小物块受力分析,如图所示:设此时的角速度为ω0,由支持力和重力的合力提供向心力,有:mgtan θ=mRω02sin θ,
解得:ω0===。
9.(1) (2)
解析 (1)当水平转盘以角速度ω1匀速转动时,绳上恰好有张力,静摩擦力达到最大值,则此时物块所需向心力恰好完全由最大静摩擦力提供,则μmg=mrω12,解得:ω1=。
(2)物块恰好离开转盘,则FN=0,物块只受重力和绳的拉力,如图所示,
mgtan θ=mω22r
tan θ=
联立解得:ω2=。
10.(1) (2)π
解析 (1)圆周运动的半径r=Lcos 30°
小球的合力提供向心力
mgtan 60°=m
解得v=
(2)竖直方向Fasin 30°=Fbsin 30°+mg
水平方向Facos 30°+Fbcos 30°=mr
当小球做圆周运动的周期减小时,a绳先达到最大拉力Fa=4mg
解得T=π。
11.(1)37° (2)2 rad/s≤ωB≤4 rad/s 见解析图
解析 (1)对小球A受力分析,由牛顿第二定律得
mAgtan θ=mAωA2rA
由几何关系知rA=sin θ
解得cos θ=
即θ=37°
(2)绳子拉力FT==2.5 N
当物块B受到的最大静摩擦力指向圆心时,转盘ωB最大
FT+μmBg=mBRωBmax2
解得ωBmax=4 rad/s
当物块B受到的最大静摩擦力背离圆心时,转盘ωB最小
FT-μmBg=mBRωBmin2
解得ωBmin=2 rad/s
水平转盘角速度ωB的取值范围为
2 rad/s≤ωB≤4 rad/s。
1.(2023·南通市高一期末)一个杯子放在水平餐桌转盘上随转盘做匀速圆周运动,角速度恒定,则( )
A.杯子受重力、支持力、摩擦力和向心力作用
B.杯子受到的摩擦力方向始终指向转盘中心
C.杯子离转盘中心越近越容易做离心运动
D.若给杯子中加水,杯子更容易做离心运动
2.如图所示,粗糙水平圆盘上,质量相等的A、B两物块叠放在一起,随圆盘一起做匀速圆周运动,则下列说法正确的是( )
A.A、B都有沿切线方向且向后滑动的趋势
B.B运动所需的向心力大于A运动所需的向心力
C.盘对B的摩擦力是B对A的摩擦力的2倍
D.若B相对圆盘先滑动,则A、B间的动摩擦因数μA小于盘与B间的动摩擦因数μB
3.某同学用硬塑料管和铁质螺丝帽研究匀速圆周运动。如图所示,该同学将螺丝帽套在塑料管上,手握塑料管使其保持竖直并在水平面内做半径为r的匀速圆周运动。假设螺丝帽与塑料管间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,重力加速度为g。下列分析正确的是( )
A.若塑料管转动速度增大,螺丝帽受到的摩擦力越大
B.当螺丝帽恰好不下滑时,手转动塑料管的角速度ω=
C.若塑料管的转动速度持续增大,螺丝帽最终会沿塑料管上滑
D.若塑料管的转动速度持续增大,地面对人的支持力始终不变
4.如图所示,底面半径为R的平底漏斗水平放置,质量为m的小球置于底面边缘紧靠侧壁,漏斗内表面光滑,侧壁的倾角为θ,重力加速度为g。现给小球一垂直于半径向里的某一初速度v0,使之在漏斗底面内做圆周运动,则( )
A.小球一定受到两个力的作用
B.小球可能受到三个力的作用
C.当v0<时,小球对底面的压力为零
D.当v0=时,小球对侧壁的压力为零
5.如图所示,正方形框ABCD竖直放置,两个完全相同的小球P、Q分别穿在方框的BC、CD边上,当方框绕AD轴匀速转动时,两球均恰与方框保持相对静止且位于BC、CD边的中点,已知两球与方框之间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力,则两球与方框间的动摩擦因数为( )
A. B. C. D.
6.如图为某游乐设施,水平转盘中央有一根可供游客抓握的绳子,质量为m的游客,到转轴的距离为r,游客和转盘间的动摩擦因数为μ,设游客受到的最大静摩擦力等于滑动摩擦力,已知重力加速度为g。
(1)当游客不抓握绳子时,为保证游客不滑动,转盘的角速度最大不能超过多少?
(2)当转盘的角速度ω=时,游客抓住绳子可使自己不滑动,则人拉绳的力至少是多大?
7.如图所示,在匀速转动的水平圆盘上,沿半径方向放着用水平细线相连的质量相等的两个物体A和B,它们分居圆心两侧,质量均为m,与圆心距离分别为RA=r,RB=2r,与盘间的动摩擦因数μ相同,重力加速度为g,设最大静摩擦力等于滑动摩擦力。当圆盘转速加快到两物体刚好还未发生滑动时,下列说法正确的是( )
A.此时绳子张力为FT=4μmg
B.此时圆盘的角速度为ω=
C.此时A所受摩擦力方向沿半径指向圆内
D.若此时烧断绳子,A仍相对盘静止,B将做离心运动
8.如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴转动的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合。转台以一定角速度匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后小物块随陶罐一起转动且相对罐壁静止,此时小物块受到的摩擦力恰好为0,且它和O点的连线与OO′之间的夹角θ为60°,重力加速度为g。求转台转动的角速度。
9.(2022·南通市高一期末)如图所示,水平转盘上放有质量为m的物块,物块到转轴的距离为r。一段绳的一端与物块相连,另一端系在圆盘中心上方r处,绳恰好伸直,物块和转盘间的动摩擦因数为μ,设物块受到的最大静摩擦力等于滑动摩擦力,已知重力加速度为g。
(1)当水平转盘以角速度ω1匀速转动时,绳上恰好有张力,求ω1的值;
(2)当水平转盘以角速度ω2匀速转动时,物块恰好离开转盘,求ω2的值。
10.(2023·南通市高一统考期末)如图所示,一质量为m的小球用长度均为L的两轻绳a、b连接,绳a的另一端固定在竖直细杆的P点,绳b的另一端固定在杆上距P点为L的Q点。当杆绕其竖直中心轴匀速转动时,将带动小球在水平面内做匀速圆周运动。不计空气阻力,重力加速度为g。
(1)当绳b刚好拉直(无弹力)时,求小球的线速度大小v;
(2)若两绳能承受的最大拉力均为4mg,求小球绕杆做圆周运动的最小周期T。
11.(2023·苏州市高一统考期中)如图甲所示,一半径为R=0.5 m的水平转盘可以绕着竖直轴OO′转动,水平转盘中心O处有一个光滑小孔,用一根长为L=1 m的细线穿过小孔将质量分别为mA=0.2 kg、mB=0.5 kg的小球A和小物块B连接。现让小球和水平转盘各以一定的角速度在水平面内转动起来,小物块B与水平转盘间的动摩擦因数μ=0.3,且始终处于水平转盘的边缘处与转盘相对静止,取g=10 m/s2,求:
(1)若小球A的角速度ω=5 rad/s,细线与竖直方向的夹角θ;
(2)在满足(1)中的条件下,通过计算给出水平转盘角速度ωB的取值范围,并在图乙中画出Ff-ω2图像(假设最大静摩擦力等于滑动摩擦力,且规定沿半径指向圆心为正方向)。
(可能使用到的数据:sin 30°=,cos 30°=,sin 37°=,cos 37°=)
专题强化练7 水平面内的圆周运动的临界问题
1.B [杯子受到重力、支持力和摩擦力三个力,向心力不是物体的实际受力,故A错误;杯子做匀速圆周运动,向心力由摩擦力提供,始终指向转盘中心,故B正确;杯子做匀速圆周运动Fn=Ff=mω2r,离转盘中心越近,所需摩擦力越小,越不容易达到最大静摩擦力,越不容易做离心运动,故C错误;根据Ff=mω2r≤μmg可知,给杯子中加水,杯子不会更容易做离心运动,故D错误。]
2.C [把A、B当成一个整体,在水平方向上只受摩擦力作用,所以,摩擦力即物块所受合外力,提供向心力,摩擦力方向指向圆心,物块有沿径向向外滑动的趋势,故A错误;物块做匀速圆周运动,向心力F=m,A、B质量相同,一起做匀速圆周运动的角速度、半径也相等,所以,两者运动所需的向心力相等,故B错误;由受力分析可知B对A的摩擦力等于F,盘对B的摩擦力等于2F,故C正确;若B相对圆盘先滑动,则2μBmg-μAmg<μAmg,即μB<μA,故D错误。]
3.D [若塑料管转动速度增大,螺丝帽受到的摩擦力不变,等于重力,螺丝帽不会沿塑料管上滑,A、C错误;对螺丝帽根据牛顿第二定律得FN=mω2r,根据平衡条件得μFN=mg,解得ω=,B错误。因系统无竖直方向加速度,无论转速多大,地面对人的支持力等于系统总重力,D正确。]
4.B [对小球,由牛顿第二定律,有
FN2sin θ=m
FN1+FN2cos θ=mg
可知侧壁对小球的支持力FN2不可能为零,底面对小球的支持力FN1可能为零。所以小球可能受到三个力的作用,也可能受到两个力的作用。由牛顿第三定律可知,小球对侧壁的压力不可能为零,所以A、D错误,B正确;当v0<时,FN1=mg->0,由牛顿第三定律可知,当v0<时,小球对底面的压力不为零,故C错误。]
5.B [设方框边长为l,小球质量为m,对P球,根据牛顿第二定律可得μmω2l=mg,对Q球,根据牛顿第二定律可得μmg=mω2,联立解得μ=,故选B。]
6.(1) (2)μmg
解析 (1)当游客受到的摩擦力达到最大静摩擦力时恰好不滑动
μmg=mω02r
得ω0=
(2)由题意有FT+μmg=mω2r
得FT=μmg
由牛顿第三定律得:
FT′=FT=μmg。
7.B [A和B随着圆盘转动时,合外力提供向心力,则F=mω2R,B的运动半径比A的半径大,所以B所需向心力大,细线拉力相等,所以当圆盘转速加快到两物体刚好还未发生滑动时,B的静摩擦力方向沿半径指向圆心,A的最大静摩擦力方向沿半径指向圆外,对物体A、B,根据牛顿第二定律分别得:FT-μmg=mω2r,FT+μmg=mω2·2r,解得:FT=3μmg,ω=,此时A所需的向心力大小为FnA=mω2r=2μmg,B所需的向心力大小为FnB=mω2·2r=4μmg,若此时烧断细线,A、B的最大静摩擦力均不足以提供物体所需向心力,则A、B均做离心运动,故B正确,A、C、D错误。]
8.
解析 对小物块受力分析,如图所示:设此时的角速度为ω0,由支持力和重力的合力提供向心力,有:mgtan θ=mRω02sin θ,
解得:ω0===。
9.(1) (2)
解析 (1)当水平转盘以角速度ω1匀速转动时,绳上恰好有张力,静摩擦力达到最大值,则此时物块所需向心力恰好完全由最大静摩擦力提供,则μmg=mrω12,解得:ω1=。
(2)物块恰好离开转盘,则FN=0,物块只受重力和绳的拉力,如图所示,
mgtan θ=mω22r
tan θ=
联立解得:ω2=。
10.(1) (2)π
解析 (1)圆周运动的半径r=Lcos 30°
小球的合力提供向心力
mgtan 60°=m
解得v=
(2)竖直方向Fasin 30°=Fbsin 30°+mg
水平方向Facos 30°+Fbcos 30°=mr
当小球做圆周运动的周期减小时,a绳先达到最大拉力Fa=4mg
解得T=π。
11.(1)37° (2)2 rad/s≤ωB≤4 rad/s 见解析图
解析 (1)对小球A受力分析,由牛顿第二定律得
mAgtan θ=mAωA2rA
由几何关系知rA=sin θ
解得cos θ=
即θ=37°
(2)绳子拉力FT==2.5 N
当物块B受到的最大静摩擦力指向圆心时,转盘ωB最大
FT+μmBg=mBRωBmax2
解得ωBmax=4 rad/s
当物块B受到的最大静摩擦力背离圆心时,转盘ωB最小
FT-μmBg=mBRωBmin2
解得ωBmin=2 rad/s
水平转盘角速度ωB的取值范围为
2 rad/s≤ωB≤4 rad/s。
