第七章 相交线与平行线 章末复习(含答案)
文档属性
| 名称 | 第七章 相交线与平行线 章末复习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章 相交线与平行线
章末复习
考点① 对顶角、余角和补角
1.如图,直线 AB,CD 相交 于点O,OE⊥AB 于点 O,OF 平分∠AOE, ∠BOD =则下列结论中不正确的是( )
A.∠AOF=45° B.∠BOD=∠AOC
C.∠BOD的余角等于 D.∠AOD与∠BOD互为补角
2.如图,直线 AB,CD EF 相交于点O;
(1)分别写出∠AOE,∠DOF 的对顶角;
(2)如果∠COE = 90°,∠BOF = 20°,∠BOD和∠AOD的度数.
3.如图,直线 AB,CD 相交于点 O,且 若OF平分
(1)求 的度数;
(2)若 求 的度数.
考点② 平行线的判定
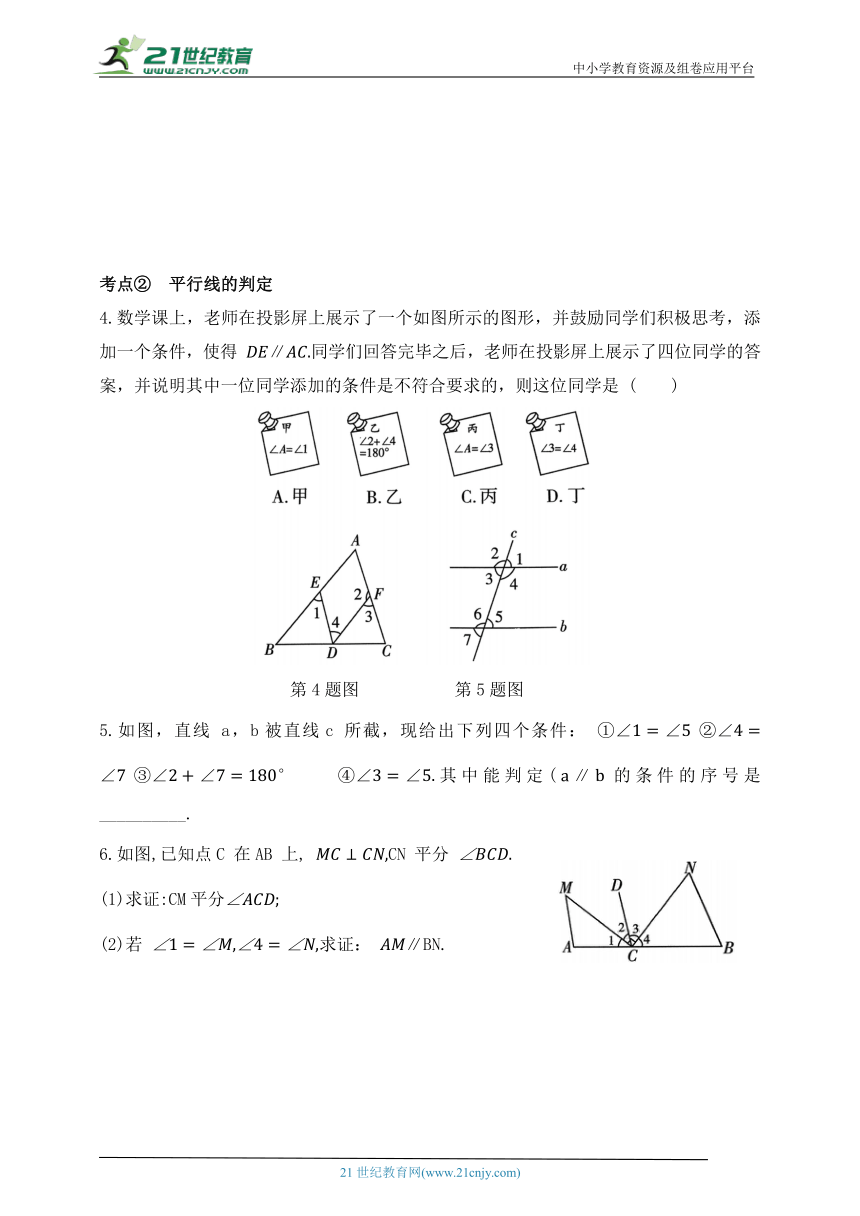
4.数学课上,老师在投影屏上展示了一个如图所示的图形,并鼓励同学们积极思考,添加一个条件,使得 ∥同学们回答完毕之后,老师在投影屏上展示了四位同学的答
案,并说明其中一位同学添加的条件是不符合要求的,则这位同学是 ( )
第4题图 第5题图
5.如图,直线 a,b被直线c 所截,现给出下列四个条件: 其中能判定(∥的条件的序号是__________.
6.如图,已知点C 在AB 上, CN 平分
(1)求证:CM平分
(2)若 求证: ∥BN.
考点③ 平行线的性质及应用
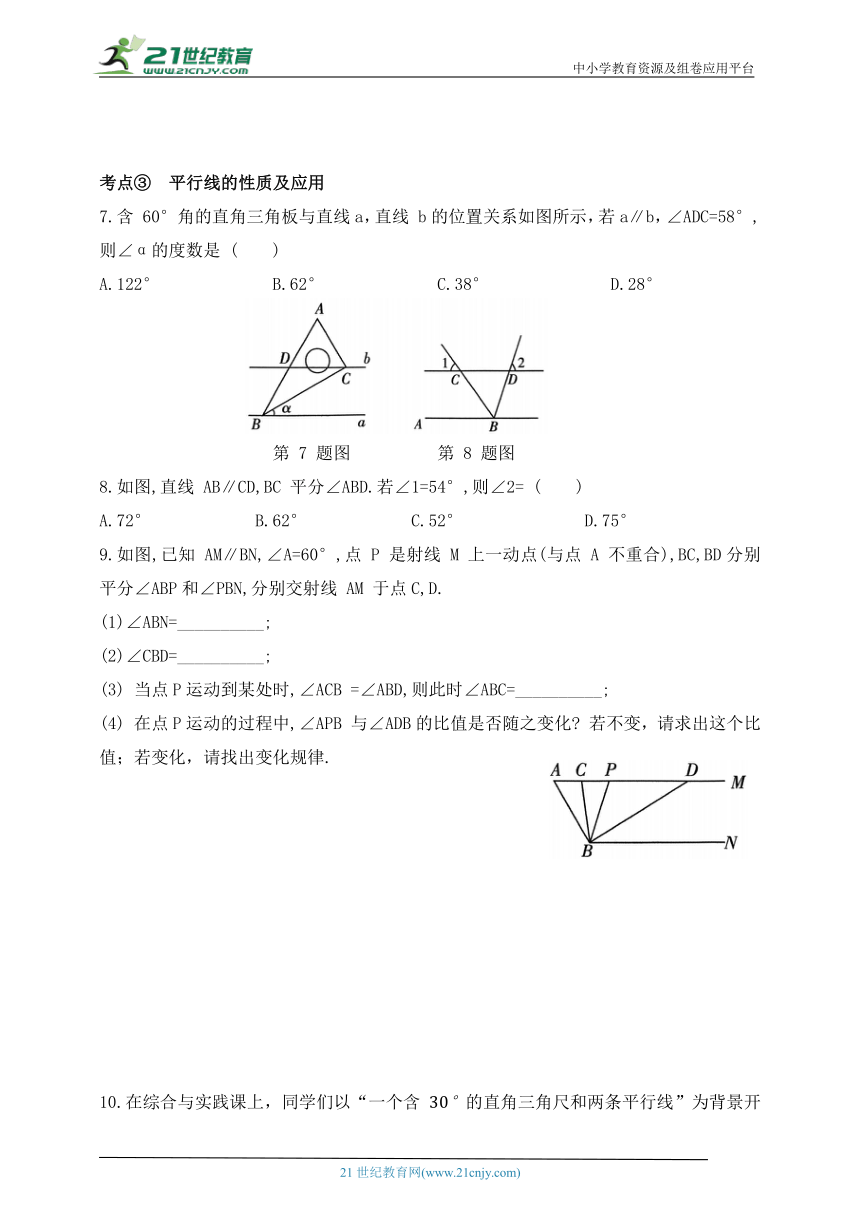
7.含 60°角的直角三角板与直线a,直线 b的位置关系如图所示,若a∥b,∠ADC=58°,则∠α的度数是 ( )
A.122° B.62° C.38° D.28°
第 7 题图 第 8 题图
8.如图,直线 AB∥CD,BC 平分∠ABD.若∠1=54°,则∠2= ( )
A.72° B.62° C.52° D.75°
9.如图,已知 AM∥BN,∠A=60°,点 P 是射线 M 上一动点(与点 A 不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线 AM 于点C,D.
(1)∠ABN=__________;
(2)∠CBD=__________;
(3) 当点P运动到某处时,∠ACB =∠ABD,则此时∠ABC=__________;
(4) 在点P运动的过程中,∠APB 与∠ADB的比值是否随之变化 若不变,请求出这个比值;若变化,请找出变化规律.
10.在综合与实践课上,同学们以“一个含 的直角三角尺和两条平行线”为背景开展数学活动,如图1,已知两直线 a,b且 和直角三角形ABC,
(1)在图1中, 求 的度数;
(2)如图2,创新小组的同学把直线 a 向上平移,改变三角形的位置,使点 A 在直线b上,点 M 在直线b上,改变 和 的位置,使 AC平分 请指出此时 与的数量关系,并说明理由;
(3)如图3,开拓小组的同学在图 1的基础上把直线 a 向上平移,并把 的位置改变,请你探究并直接写出 与 的数量关系.
考点④ “拐点”问题
11.如图,直线 m∥n,若∠1=65°,则∠2-∠3的度数为 ( )
A.115° B.120° C.125° D.130°
第 11题图 第 12 题图
12.如图,直线 则∠1+∠2= ( )
A.30° B.35° C.36° D.40°
13.已知AB∥CD,P 为直线 AB,CD所确定的平面内一点.
(1)如图1,∠P,∠A,∠C 之间的数量关系为___________;
(2)如图2,求证:∠APC=∠C-∠A;
(3)如图3,点 E 在直线 AB 上,若∠APC=20°,∠PAB=30°,过点 E 作 EF∥PC,作∠PEG=∠PEF,∠BEG的平分线交 PC 于点 H,直接写出∠PEH 的度数.
考点⑤ 尺规作角
14.如图,已知 用尺规作图作 使 不写作法,但要保留作图痕迹.
15.如图, ∥点E 是射线CD上一点.
(1)在射线AB上取点F,利用尺规作图,使(保留作图痕迹,不要求写作法);
与相等吗 说明理由.
考点⑥ 易错易混点
16.下列结论正确的是 ( )
A.过一点有且只有一条直线与已知直线垂直
B.过一点有且只有一条直线与已知直线平行
C.在同一平面内,不相交的两条射线是平行线
D.如果两条直线都与第三条直线平行,那么这两条直线互相平行
参考答案
1. C
2.解:(1)∠AOE的对顶角是∠BOF, ∠DOF 的对顶角是∠COE;
(2)因为∠COE=90°,∠BOF=20°,所以∠DOF=∠COE=90°,∠AOE=∠BOF=20°,
所以∠BOD=∠FOD-∠FOB=90°-20°=70°,所以∠AOD=180°-∠BOD=110°.
3.解:(1)因为直线 AB, CD 相交 于 点 O,且∠BOC=96°,所以∠AOD=∠BOC=96°,
因为 OF 平分∠AOD,所以
所以∠COF=180°-∠DOF=132°;
(2)因为 OE⊥OF,所以∠FOE= 90°,
因为∠DOF=48°,所以∠DOE=42°,
所以∠BOE=180°-∠BOC-∠DOE=42°.
4. C 5.①③④
6.证明:(1)因为 CN平分∠BCD,所以∠3=∠4,
因为 MC⊥CN,所以∠2+∠3=90°所以∠1+∠4=90°,
所以∠1=∠2,所以CM平分∠ACD;
(2)由(1)知∠1=∠2,∠3=∠4,
因为∠1=∠M,∠4=∠N,所以∠2=∠M,∠3=∠N,
所以AM∥CD,CD∥BN,所以 AM∥BN.
7. D 8. A
9.解:(1)因为 AM∥BN,所以∠ABN+∠A= 180°,
因为∠A= 60°,所以∠ABN=180°- 60°= 120°,
故答案为: 120°;
(2)因为∠ABN=120°,所以∠ABP+∠PBN=120°,
因为 BC,BD 分别平分∠ABP 和∠PBN ,所以∠ABP=2∠CBP,∠PBN= 2∠DBP,
所以2∠CBP +2∠DBP=120°,所以∠CBD=∠CBP+∠DBP=60°;
故答案为: 60°;
(3)因为 AM∥BN,所以∠ACB=∠CBN,
因为∠ACB=∠ABD,所以∠CBN=∠ABD,
所以∠ABC+∠CBD=∠CBD+∠DBN,所以∠ABC=∠DBN;
由(2)可知∠ABN=120°,∠CBD=60°,所以∠ABC+∠DBN=∠ABN-∠CBD=120°-60°=60°,
所以∠ABC=30°;
故答案为:30°;
(4)不变.∠APB:∠ADB= 2:1.
因为 AM∥BN,所以∠APB=∠PBN,∠ADB=∠DBN,
因为 BD平分∠PBN,所以∠PBN= 2∠DBN ,所以∠APB:∠ADB= 2:1.
10.解:(1)如图1,因为∠BCA=90°,∠1= 46°,
所以∠3= 180°-90°-∠1= 44°,
因为a∥b.所以∠2=∠3=44°;
(2)∠1=∠2;
理由如下:过点C作CE∥a,
因为 AC 平分∠BAM,所以∠BAM=2∠BAC=60°,∠CAM=30°,所以∠2=∠BCE,
因为a∥b,CE∥a,所以CE∥b,∠1=∠BAM=60°,所以∠ECA=∠CAM=30°,
所以∠2=∠BCE=90°-∠ECA=60°,所以∠1=∠2;
(3)∠2-∠1= 120°.
理由如下: 过点 B 作 BD∥a,则∠ABD=180°-∠2,
因为a∥b, BD∥a,所以 BD∥b,所以∠DBC=∠1,
因为∠ABC= 60°,所以180°-∠2+∠1= 60°,所以∠2-∠1=120°.
11. A 12. A
13.解:(1)过点 P作∥如图 1:
因为 ∥所以 ∥∥所以
所以
故答案为:∠P=∠A+∠C;
(2)证明:如图 2,过点 P 作 PM∥AB.
因为 ∥所以
因为AB∥CD,MP∥AB,所以 PM∥CD,所以
因为∠APC=∠MPC-∠MPA,所以∠APC=∠C-∠A;
(3)∠PEH的度数为 25°.
理由如下:如图 3:
因为 又因为由(2)知,
所以
又因为 ∥所以
因为 ∥所以
因为 的平分线 交PC 于点 H,
所以
所以
14.解:如图, 即为所求作.
15.解:(1)
(2)相等,理由如下:
因为 ∥所以
因为 所以
16. D 解析:A.过一点有且只有一条直线与已知直线垂直,应强调在同一平面内,故 A 错误;B.过一点有且只有一条直线与已知直线平行,应强调在经过直线外一点,故 B 错误的;C.在同一平面内,不相交的两条直线是平行线,射线不一定,故C 错误;D. 如果两条直线都与第三条直线平行,那么这两条直线也互相,故 D正确.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章 相交线与平行线
章末复习
考点① 对顶角、余角和补角
1.如图,直线 AB,CD 相交 于点O,OE⊥AB 于点 O,OF 平分∠AOE, ∠BOD =则下列结论中不正确的是( )
A.∠AOF=45° B.∠BOD=∠AOC
C.∠BOD的余角等于 D.∠AOD与∠BOD互为补角
2.如图,直线 AB,CD EF 相交于点O;
(1)分别写出∠AOE,∠DOF 的对顶角;
(2)如果∠COE = 90°,∠BOF = 20°,∠BOD和∠AOD的度数.
3.如图,直线 AB,CD 相交于点 O,且 若OF平分
(1)求 的度数;
(2)若 求 的度数.
考点② 平行线的判定
4.数学课上,老师在投影屏上展示了一个如图所示的图形,并鼓励同学们积极思考,添加一个条件,使得 ∥同学们回答完毕之后,老师在投影屏上展示了四位同学的答
案,并说明其中一位同学添加的条件是不符合要求的,则这位同学是 ( )
第4题图 第5题图
5.如图,直线 a,b被直线c 所截,现给出下列四个条件: 其中能判定(∥的条件的序号是__________.
6.如图,已知点C 在AB 上, CN 平分
(1)求证:CM平分
(2)若 求证: ∥BN.
考点③ 平行线的性质及应用
7.含 60°角的直角三角板与直线a,直线 b的位置关系如图所示,若a∥b,∠ADC=58°,则∠α的度数是 ( )
A.122° B.62° C.38° D.28°
第 7 题图 第 8 题图
8.如图,直线 AB∥CD,BC 平分∠ABD.若∠1=54°,则∠2= ( )
A.72° B.62° C.52° D.75°
9.如图,已知 AM∥BN,∠A=60°,点 P 是射线 M 上一动点(与点 A 不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线 AM 于点C,D.
(1)∠ABN=__________;
(2)∠CBD=__________;
(3) 当点P运动到某处时,∠ACB =∠ABD,则此时∠ABC=__________;
(4) 在点P运动的过程中,∠APB 与∠ADB的比值是否随之变化 若不变,请求出这个比值;若变化,请找出变化规律.
10.在综合与实践课上,同学们以“一个含 的直角三角尺和两条平行线”为背景开展数学活动,如图1,已知两直线 a,b且 和直角三角形ABC,
(1)在图1中, 求 的度数;
(2)如图2,创新小组的同学把直线 a 向上平移,改变三角形的位置,使点 A 在直线b上,点 M 在直线b上,改变 和 的位置,使 AC平分 请指出此时 与的数量关系,并说明理由;
(3)如图3,开拓小组的同学在图 1的基础上把直线 a 向上平移,并把 的位置改变,请你探究并直接写出 与 的数量关系.
考点④ “拐点”问题
11.如图,直线 m∥n,若∠1=65°,则∠2-∠3的度数为 ( )
A.115° B.120° C.125° D.130°
第 11题图 第 12 题图
12.如图,直线 则∠1+∠2= ( )
A.30° B.35° C.36° D.40°
13.已知AB∥CD,P 为直线 AB,CD所确定的平面内一点.
(1)如图1,∠P,∠A,∠C 之间的数量关系为___________;
(2)如图2,求证:∠APC=∠C-∠A;
(3)如图3,点 E 在直线 AB 上,若∠APC=20°,∠PAB=30°,过点 E 作 EF∥PC,作∠PEG=∠PEF,∠BEG的平分线交 PC 于点 H,直接写出∠PEH 的度数.
考点⑤ 尺规作角
14.如图,已知 用尺规作图作 使 不写作法,但要保留作图痕迹.
15.如图, ∥点E 是射线CD上一点.
(1)在射线AB上取点F,利用尺规作图,使(保留作图痕迹,不要求写作法);
与相等吗 说明理由.
考点⑥ 易错易混点
16.下列结论正确的是 ( )
A.过一点有且只有一条直线与已知直线垂直
B.过一点有且只有一条直线与已知直线平行
C.在同一平面内,不相交的两条射线是平行线
D.如果两条直线都与第三条直线平行,那么这两条直线互相平行
参考答案
1. C
2.解:(1)∠AOE的对顶角是∠BOF, ∠DOF 的对顶角是∠COE;
(2)因为∠COE=90°,∠BOF=20°,所以∠DOF=∠COE=90°,∠AOE=∠BOF=20°,
所以∠BOD=∠FOD-∠FOB=90°-20°=70°,所以∠AOD=180°-∠BOD=110°.
3.解:(1)因为直线 AB, CD 相交 于 点 O,且∠BOC=96°,所以∠AOD=∠BOC=96°,
因为 OF 平分∠AOD,所以
所以∠COF=180°-∠DOF=132°;
(2)因为 OE⊥OF,所以∠FOE= 90°,
因为∠DOF=48°,所以∠DOE=42°,
所以∠BOE=180°-∠BOC-∠DOE=42°.
4. C 5.①③④
6.证明:(1)因为 CN平分∠BCD,所以∠3=∠4,
因为 MC⊥CN,所以∠2+∠3=90°所以∠1+∠4=90°,
所以∠1=∠2,所以CM平分∠ACD;
(2)由(1)知∠1=∠2,∠3=∠4,
因为∠1=∠M,∠4=∠N,所以∠2=∠M,∠3=∠N,
所以AM∥CD,CD∥BN,所以 AM∥BN.
7. D 8. A
9.解:(1)因为 AM∥BN,所以∠ABN+∠A= 180°,
因为∠A= 60°,所以∠ABN=180°- 60°= 120°,
故答案为: 120°;
(2)因为∠ABN=120°,所以∠ABP+∠PBN=120°,
因为 BC,BD 分别平分∠ABP 和∠PBN ,所以∠ABP=2∠CBP,∠PBN= 2∠DBP,
所以2∠CBP +2∠DBP=120°,所以∠CBD=∠CBP+∠DBP=60°;
故答案为: 60°;
(3)因为 AM∥BN,所以∠ACB=∠CBN,
因为∠ACB=∠ABD,所以∠CBN=∠ABD,
所以∠ABC+∠CBD=∠CBD+∠DBN,所以∠ABC=∠DBN;
由(2)可知∠ABN=120°,∠CBD=60°,所以∠ABC+∠DBN=∠ABN-∠CBD=120°-60°=60°,
所以∠ABC=30°;
故答案为:30°;
(4)不变.∠APB:∠ADB= 2:1.
因为 AM∥BN,所以∠APB=∠PBN,∠ADB=∠DBN,
因为 BD平分∠PBN,所以∠PBN= 2∠DBN ,所以∠APB:∠ADB= 2:1.
10.解:(1)如图1,因为∠BCA=90°,∠1= 46°,
所以∠3= 180°-90°-∠1= 44°,
因为a∥b.所以∠2=∠3=44°;
(2)∠1=∠2;
理由如下:过点C作CE∥a,
因为 AC 平分∠BAM,所以∠BAM=2∠BAC=60°,∠CAM=30°,所以∠2=∠BCE,
因为a∥b,CE∥a,所以CE∥b,∠1=∠BAM=60°,所以∠ECA=∠CAM=30°,
所以∠2=∠BCE=90°-∠ECA=60°,所以∠1=∠2;
(3)∠2-∠1= 120°.
理由如下: 过点 B 作 BD∥a,则∠ABD=180°-∠2,
因为a∥b, BD∥a,所以 BD∥b,所以∠DBC=∠1,
因为∠ABC= 60°,所以180°-∠2+∠1= 60°,所以∠2-∠1=120°.
11. A 12. A
13.解:(1)过点 P作∥如图 1:
因为 ∥所以 ∥∥所以
所以
故答案为:∠P=∠A+∠C;
(2)证明:如图 2,过点 P 作 PM∥AB.
因为 ∥所以
因为AB∥CD,MP∥AB,所以 PM∥CD,所以
因为∠APC=∠MPC-∠MPA,所以∠APC=∠C-∠A;
(3)∠PEH的度数为 25°.
理由如下:如图 3:
因为 又因为由(2)知,
所以
又因为 ∥所以
因为 ∥所以
因为 的平分线 交PC 于点 H,
所以
所以
14.解:如图, 即为所求作.
15.解:(1)
(2)相等,理由如下:
因为 ∥所以
因为 所以
16. D 解析:A.过一点有且只有一条直线与已知直线垂直,应强调在同一平面内,故 A 错误;B.过一点有且只有一条直线与已知直线平行,应强调在经过直线外一点,故 B 错误的;C.在同一平面内,不相交的两条直线是平行线,射线不一定,故C 错误;D. 如果两条直线都与第三条直线平行,那么这两条直线也互相,故 D正确.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
