青岛版九上数学第1章 图形的相似第2节《怎样判定三角形相似》教学课件(共15张PPT)
文档属性
| 名称 | 青岛版九上数学第1章 图形的相似第2节《怎样判定三角形相似》教学课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 347.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-01 00:00:00 | ||
图片预览




文档简介
课件15张PPT。1.2 怎样判定三角形相似
第1课时1.理解第9个基本事实.
2.知道当△ABC与△DEF的相似比为k时,△DEF与△ABC
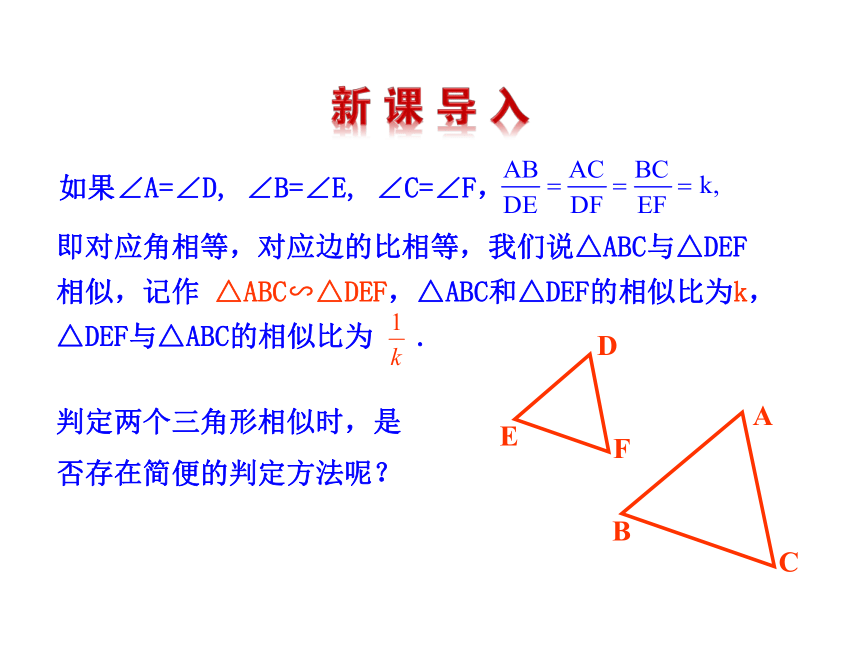
的相似比为 .即对应角相等,对应边的比相等,我们说△ABC与△DEF
相似,记作 △ABC∽△DEF,△ABC和△DEF的相似比为k,
△DEF与△ABC的相似比为 .如果∠A=∠D, ∠B=∠E, ∠C=∠F,判定两个三角形相似时,是否存在简便的判定方法呢?问题 如图l1∥l2 ∥ l3,你能否发现在两直线a,b上截得的线段有什么关系? l3 l1l2ABDEFHab通过计算可以得到:由此可得到:第9个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.说明: ①条件是“两条直线被一组平行线所截”.
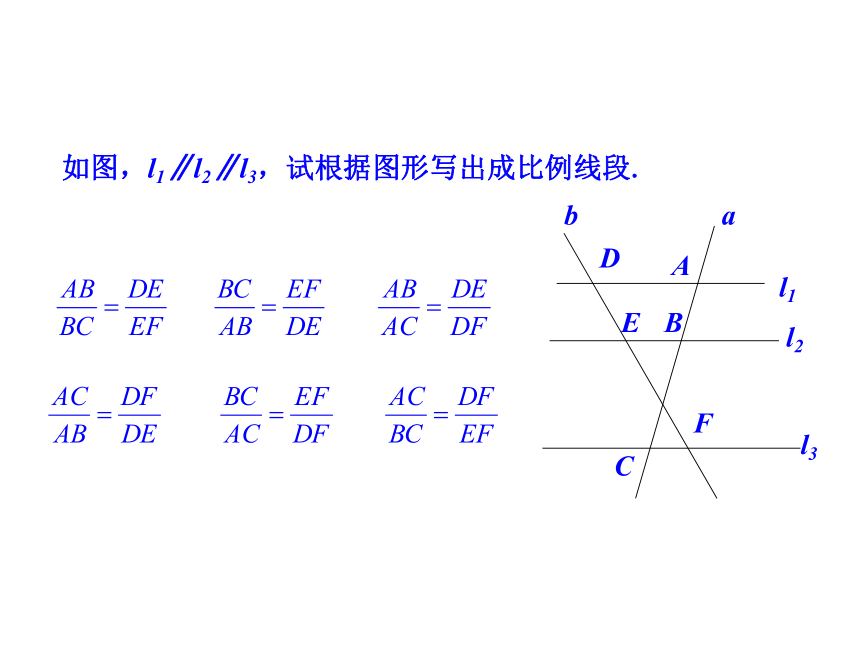
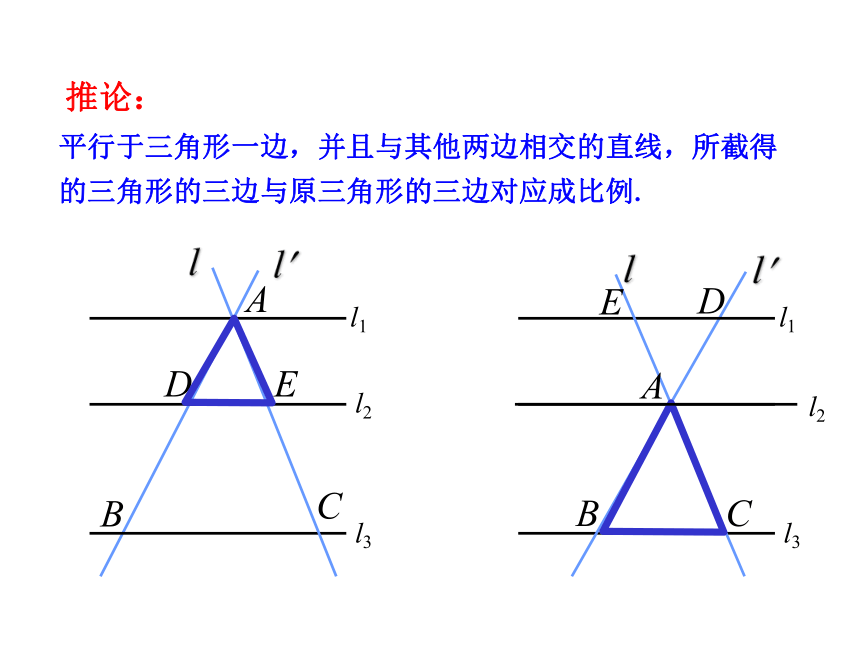
②结论是“对应线段成比例”,注意“对应”两字.强化“对应”两字的理解和记忆,如图如图,l1∥l2∥l3,试根据图形写出成比例线段.平行于三角形一边,并且与其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.推论:l2如图,DE∥BC,△ADE与△ABC有什么关系?说明理由.相似.ABCDE理由:在△ADE与△ABC中,∠A= ∠A,∵ DE∥BC∴∠ADE=∠B, ∠AED=∠C,过E作EF∥AB交BC于F,∵四边形DBFE是平行四边形,F∴DE=BF.∴△ADE∽△ABC.探究平行于三角形一边的直线与其他两边(或延长线)相交,所得
的三角形与原三角形________.相似“A”型 “X”型 图中共有____对相似三角形.已知:如图,AB∥EF∥CD,3△EOF∽△CODAB∥EF △AOB∽△FOE AB∥CDEF∥CD△AOB∽△DOC【跟踪训练】1.(滨州·中考)如图,A,B两点被池塘隔开,在AB
外取一点C,连接AC、BC,在AC上取点M,使AM=3MC,作
MN∥AB交BC于N,量得MN=38cm,则AB的长为 . 152cm2.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG﹕BC=_______.△ADG∽△AEH∽△AFI∽△ABC1﹕4 3.如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解析:与△ABC相似的三角形有3个: △ADE
△GFC
△GOE4.如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小. (2)求DE的长.ADBEC(2)由(1)知△ADE∽△ABC,通过本节课的学习,需要掌握
1.第9个基本事实及其推论的应用.
2.判定三角形相似的方法.
第1课时1.理解第9个基本事实.
2.知道当△ABC与△DEF的相似比为k时,△DEF与△ABC
的相似比为 .即对应角相等,对应边的比相等,我们说△ABC与△DEF
相似,记作 △ABC∽△DEF,△ABC和△DEF的相似比为k,
△DEF与△ABC的相似比为 .如果∠A=∠D, ∠B=∠E, ∠C=∠F,判定两个三角形相似时,是否存在简便的判定方法呢?问题 如图l1∥l2 ∥ l3,你能否发现在两直线a,b上截得的线段有什么关系? l3 l1l2ABDEFHab通过计算可以得到:由此可得到:第9个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.说明: ①条件是“两条直线被一组平行线所截”.
②结论是“对应线段成比例”,注意“对应”两字.强化“对应”两字的理解和记忆,如图如图,l1∥l2∥l3,试根据图形写出成比例线段.平行于三角形一边,并且与其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.推论:l2如图,DE∥BC,△ADE与△ABC有什么关系?说明理由.相似.ABCDE理由:在△ADE与△ABC中,∠A= ∠A,∵ DE∥BC∴∠ADE=∠B, ∠AED=∠C,过E作EF∥AB交BC于F,∵四边形DBFE是平行四边形,F∴DE=BF.∴△ADE∽△ABC.探究平行于三角形一边的直线与其他两边(或延长线)相交,所得
的三角形与原三角形________.相似“A”型 “X”型 图中共有____对相似三角形.已知:如图,AB∥EF∥CD,3△EOF∽△CODAB∥EF △AOB∽△FOE AB∥CDEF∥CD△AOB∽△DOC【跟踪训练】1.(滨州·中考)如图,A,B两点被池塘隔开,在AB
外取一点C,连接AC、BC,在AC上取点M,使AM=3MC,作
MN∥AB交BC于N,量得MN=38cm,则AB的长为 . 152cm2.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG﹕BC=_______.△ADG∽△AEH∽△AFI∽△ABC1﹕4 3.如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解析:与△ABC相似的三角形有3个: △ADE
△GFC
△GOE4.如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小. (2)求DE的长.ADBEC(2)由(1)知△ADE∽△ABC,通过本节课的学习,需要掌握
1.第9个基本事实及其推论的应用.
2.判定三角形相似的方法.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
