青岛版九上数学第1章《图形的相似》复习课件(共32张PPT)
文档属性
| 名称 | 青岛版九上数学第1章《图形的相似》复习课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 349.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-01 00:00:00 | ||
图片预览





文档简介
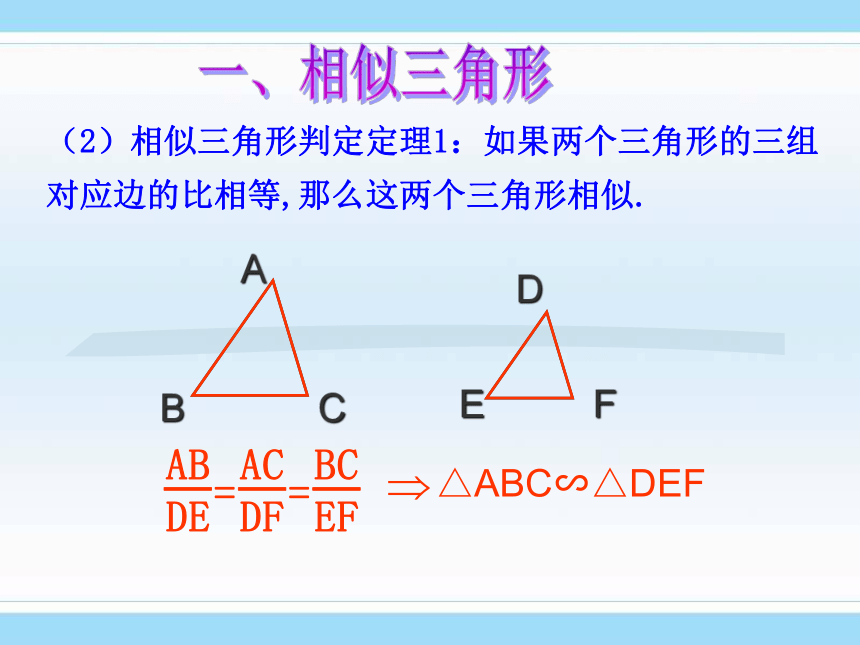
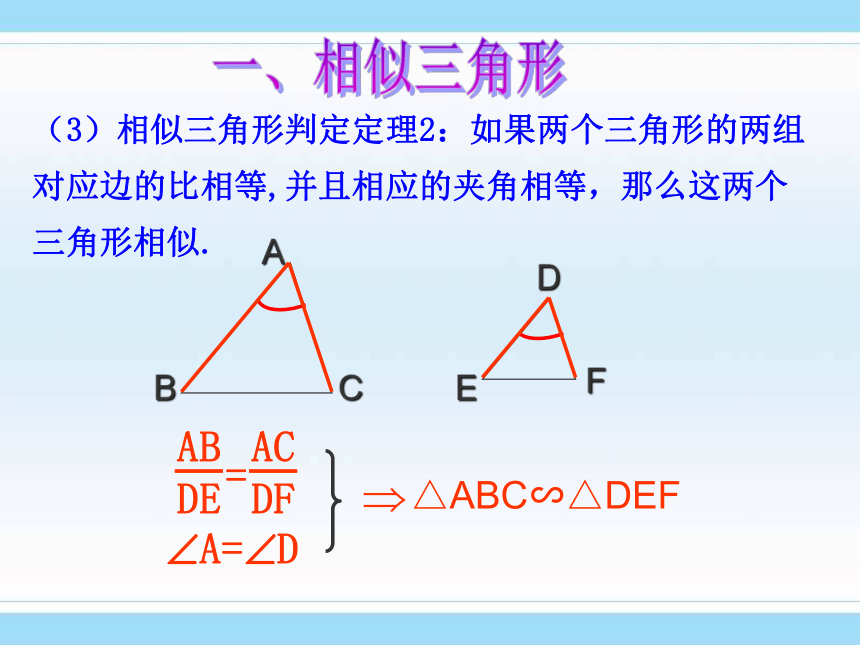
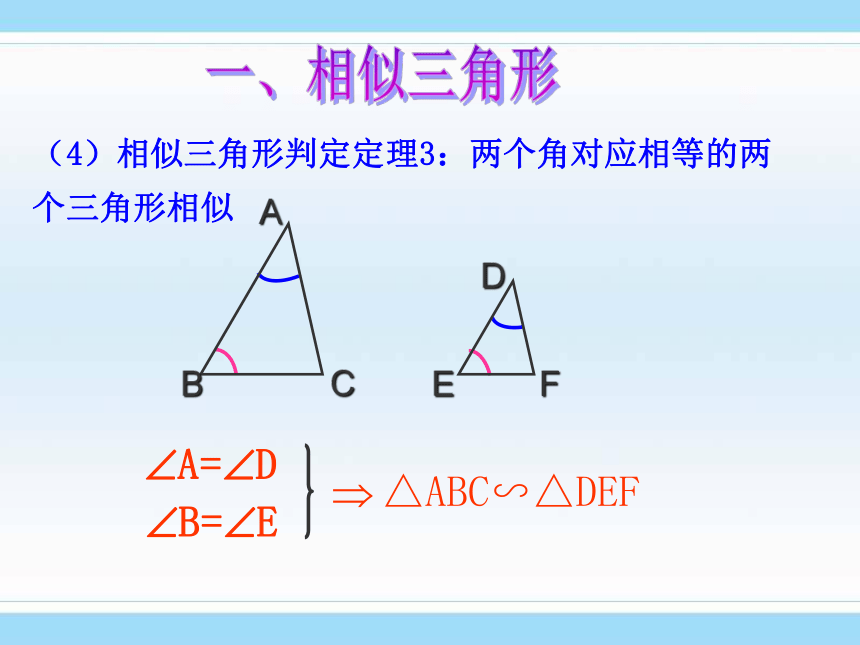
课件32张PPT。第1章《图形的相似》1 定义:相似比:相似三角形的对应边的比,叫做相似三角形的相似比。一、相似三角形知识点复习 三组对应角相等,三组对应边的比相等的两个三角形是相似三角形 .2 三角形相似的判定方法有哪几种?(1)预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。∵DE∥BC, ∴△ADE∽△ABC一、相似三角形(2)相似三角形判定定理1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.△ABC∽△DEF一、相似三角形(3)相似三角形判定定理2:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.一、相似三角形(4)相似三角形判定定理3:两个角对应相等的两个三角形相似一、相似三角形2 相似三角形的判定:(1)预备定理;
(2)判定定理一;
(3)判定定理二;
(4)判定定理三;一、相似三角形3 相似三角形的性质:一、相似三角形(1) 相似三角形的对应角相等,对应边的比相等.
(2 )相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
(3 )相似三角形周长的比等于相似比,
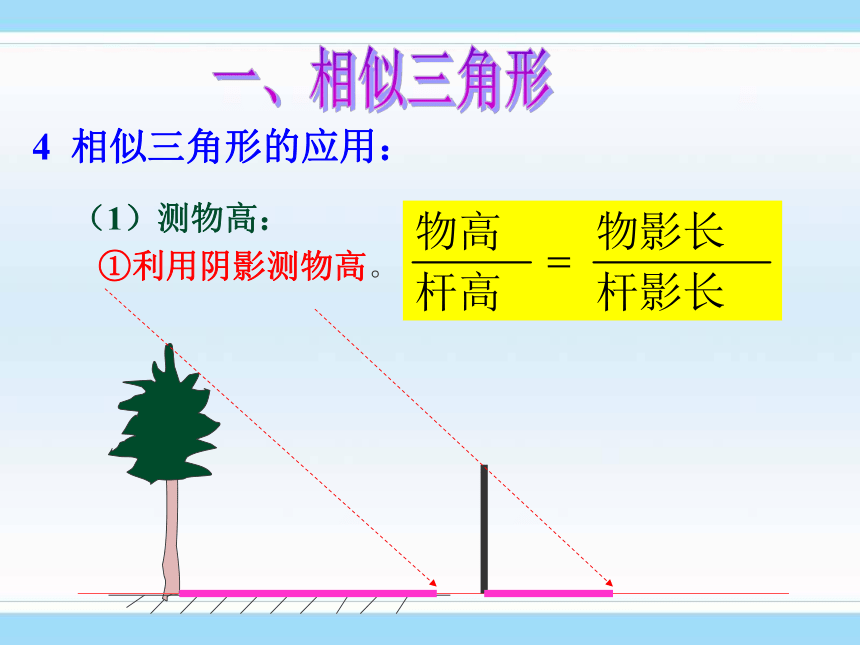
(4) 相似三角形面积比等于相似比的平方.(1)测物高:
①利用阴影测物高。
一、相似三角形4 相似三角形的应用:(1)测物高:
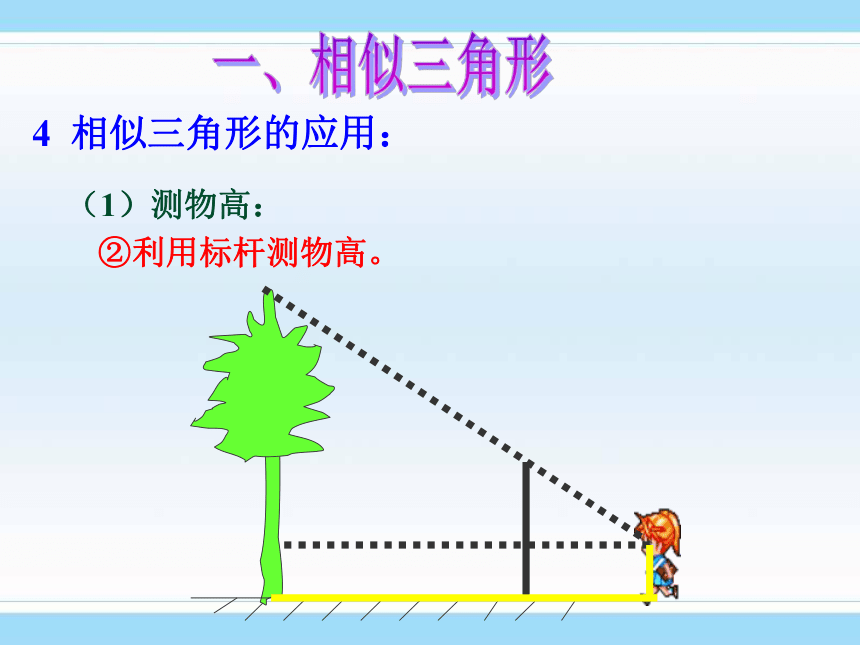
②利用标杆测物高。
一、相似三角形4 相似三角形的应用:(1)测物高:
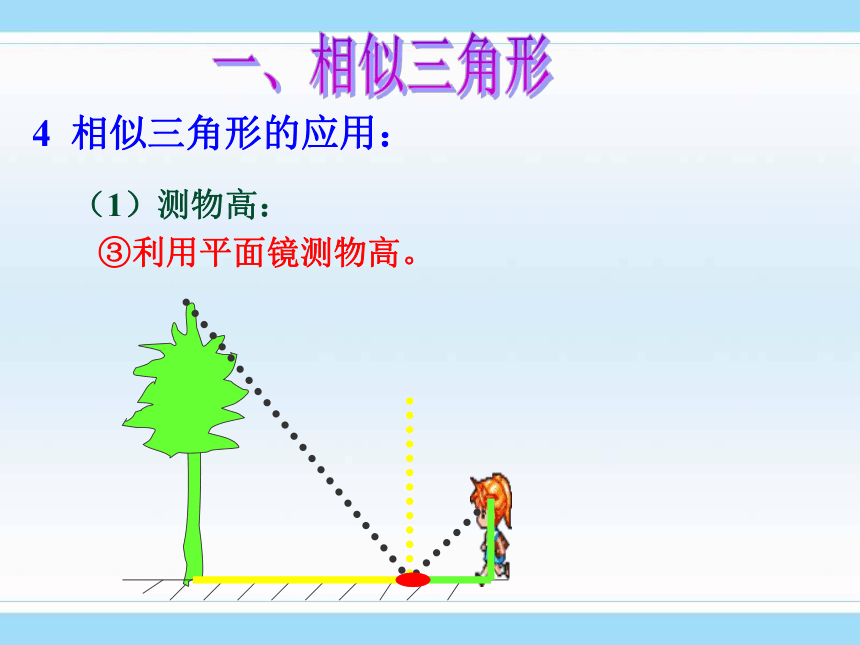
③利用平面镜测物高。
一、相似三角形4 相似三角形的应用:(1)测物宽:
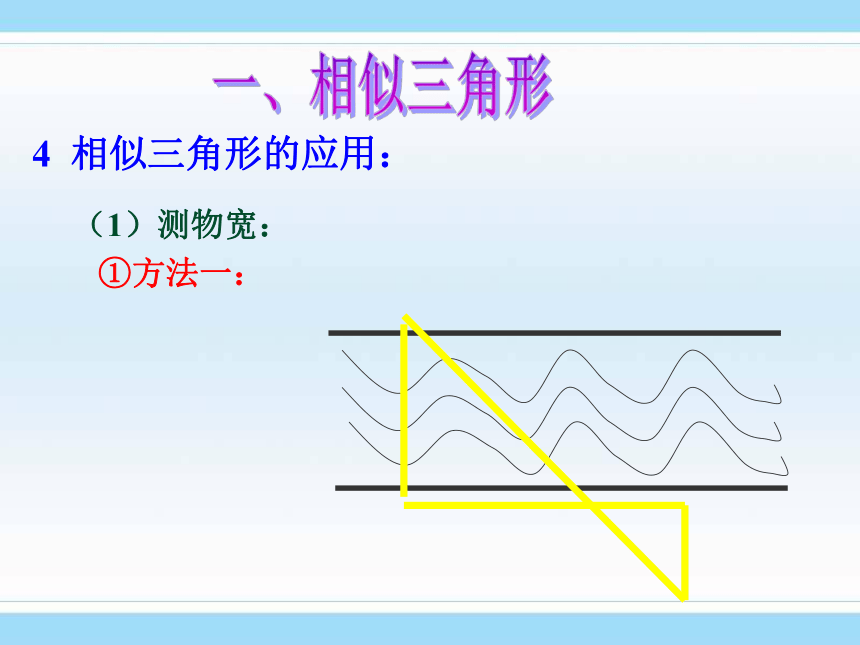
①方法一:
一、相似三角形4 相似三角形的应用:(1)测物宽:
①方法二:
一、相似三角形4 相似三角形的应用:二、相似多边形 如果两个多边形满足各对应角相等,各对应边的比相等,那么这两个多边形相似.1 相似多边形的定义:2 相似多边形的判定: 如果两个多边形满足各对应角相等,各对应边的比相等,那么这两个多边形相似.知识要点二、相似多边形3 相似多边形的性质:(1)相似多边形对应角相等,对应边的比相等.
(2)相似多边形周长的比等于相似比.
(3)相似多边形面积的比等于相似比的平方.1、 两个多边形不仅相似,而且对应顶点的连线相交于一点,这样的相似叫做位似,点O叫做位似中心.2、利用位似的方法,可以把一个多边形放大或缩小知识要点3三、位似(1)如何作位似图形(放大).(3)体会位似图形何时为正像何时为倒像.(2)如何作位似图形(缩小).3 位似变换的性质: 位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.4 位似变换中对应点的坐标变化规律:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.或AP:AC=AC:AB1、如图点P是△ABC的AB边上的一点,要使△APC∽△ACB,
则需补上哪一个条件? 复习题2、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________3.找一找:(1) 如图1,已知:DE∥BC,EF ∥AB,则图中共有_____对三角形相似.(2) 如图2,已知:△ABC中, ∠ACB=900 ,CD⊥ AB于D,DE⊥BC于E,则图中共有_____个三角形和△ABC相似.34C5、若△ ACP∽△ABC,AP=4,BP=5,则AC=_______,△ ACP与△ABC的相似比是_______,周长之比是_______,面积之比是_______。62 : 32 : 34 : 96、如图,DE∥BC,EF∥AB,且S△ADE=25,S△CEF=36.
求△ABC的面积.解:∵DE∥BC,EF∥AB∴∠A=∠CEF,∠AED=∠C∴△ADE∽△EFC∴∵DE∥BC∴△ADE∽△ABC∵ S△ADE=25∴S △ABC=121∴∴∴7、在平行四边形ABCD中,AE:BE=1:2.若S△AEF=6cm2,则S△CDF = cm254S △ADF=____cm218
8、如图(6), △ABC中,DE??FG??BC,
AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=_________
答案:1:3:59、如图,正方形ABCD中,E是DC中点,FC= BC.
求证: AE⊥EF证明:∵四边形ABCD是正方形∴BC=CD=AD,∠D=∠C=90°∵E是BC中点,FC= BC∴∴∴△ADE∽△ECF∴∠1=∠2∵∠D=90°∴∠1+ ∠3=90 °∴∠2+ ∠3=90°∴ AE⊥EF画一画10、 在方格纸中,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.在如图4×4的格纸中, △ABC是一个格点三角形(1)在右图中,请你画一个格点三角形,使它与△ABC相似(相似比不为1)11、在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为X米,则
答:楼高36米.12、如图,教学楼旁边有一棵树,数学小组的同学们想利用树影测量树高。课外活动时在阳光下他们测得一根长为1米的竹杆的影长是0.9米,当他们马上测量树的影子长时,发现树的影子不全落在地面上,于是他们测得落在地面上的影子长2.7米,落在墙壁上的影长1.2米,求树的高度. 13、皮皮欲测楼房高度,他借助一长5m的标竿,当楼房顶部、标竿顶端与他的眼睛在一条直线 上时,其他人测出AB=4cm,AC=12m。已知皮皮眼睛离地面1.6m.请你帮他算出楼房的高度。
(2)判定定理一;
(3)判定定理二;
(4)判定定理三;一、相似三角形3 相似三角形的性质:一、相似三角形(1) 相似三角形的对应角相等,对应边的比相等.
(2 )相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
(3 )相似三角形周长的比等于相似比,
(4) 相似三角形面积比等于相似比的平方.(1)测物高:
①利用阴影测物高。
一、相似三角形4 相似三角形的应用:(1)测物高:
②利用标杆测物高。
一、相似三角形4 相似三角形的应用:(1)测物高:
③利用平面镜测物高。
一、相似三角形4 相似三角形的应用:(1)测物宽:
①方法一:
一、相似三角形4 相似三角形的应用:(1)测物宽:
①方法二:
一、相似三角形4 相似三角形的应用:二、相似多边形 如果两个多边形满足各对应角相等,各对应边的比相等,那么这两个多边形相似.1 相似多边形的定义:2 相似多边形的判定: 如果两个多边形满足各对应角相等,各对应边的比相等,那么这两个多边形相似.知识要点二、相似多边形3 相似多边形的性质:(1)相似多边形对应角相等,对应边的比相等.
(2)相似多边形周长的比等于相似比.
(3)相似多边形面积的比等于相似比的平方.1、 两个多边形不仅相似,而且对应顶点的连线相交于一点,这样的相似叫做位似,点O叫做位似中心.2、利用位似的方法,可以把一个多边形放大或缩小知识要点3三、位似(1)如何作位似图形(放大).(3)体会位似图形何时为正像何时为倒像.(2)如何作位似图形(缩小).3 位似变换的性质: 位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.4 位似变换中对应点的坐标变化规律:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.或AP:AC=AC:AB1、如图点P是△ABC的AB边上的一点,要使△APC∽△ACB,
则需补上哪一个条件? 复习题2、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________3.找一找:(1) 如图1,已知:DE∥BC,EF ∥AB,则图中共有_____对三角形相似.(2) 如图2,已知:△ABC中, ∠ACB=900 ,CD⊥ AB于D,DE⊥BC于E,则图中共有_____个三角形和△ABC相似.34C5、若△ ACP∽△ABC,AP=4,BP=5,则AC=_______,△ ACP与△ABC的相似比是_______,周长之比是_______,面积之比是_______。62 : 32 : 34 : 96、如图,DE∥BC,EF∥AB,且S△ADE=25,S△CEF=36.
求△ABC的面积.解:∵DE∥BC,EF∥AB∴∠A=∠CEF,∠AED=∠C∴△ADE∽△EFC∴∵DE∥BC∴△ADE∽△ABC∵ S△ADE=25∴S △ABC=121∴∴∴7、在平行四边形ABCD中,AE:BE=1:2.若S△AEF=6cm2,则S△CDF = cm254S △ADF=____cm218
8、如图(6), △ABC中,DE??FG??BC,
AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=_________
答案:1:3:59、如图,正方形ABCD中,E是DC中点,FC= BC.
求证: AE⊥EF证明:∵四边形ABCD是正方形∴BC=CD=AD,∠D=∠C=90°∵E是BC中点,FC= BC∴∴∴△ADE∽△ECF∴∠1=∠2∵∠D=90°∴∠1+ ∠3=90 °∴∠2+ ∠3=90°∴ AE⊥EF画一画10、 在方格纸中,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.在如图4×4的格纸中, △ABC是一个格点三角形(1)在右图中,请你画一个格点三角形,使它与△ABC相似(相似比不为1)11、在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为X米,则
答:楼高36米.12、如图,教学楼旁边有一棵树,数学小组的同学们想利用树影测量树高。课外活动时在阳光下他们测得一根长为1米的竹杆的影长是0.9米,当他们马上测量树的影子长时,发现树的影子不全落在地面上,于是他们测得落在地面上的影子长2.7米,落在墙壁上的影长1.2米,求树的高度. 13、皮皮欲测楼房高度,他借助一长5m的标竿,当楼房顶部、标竿顶端与他的眼睛在一条直线 上时,其他人测出AB=4cm,AC=12m。已知皮皮眼睛离地面1.6m.请你帮他算出楼房的高度。
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
