人教版数学八年级下册第十八章 平行四边形 章末复习学案(含答案)
文档属性
| 名称 | 人教版数学八年级下册第十八章 平行四边形 章末复习学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 258.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-15 10:51:28 | ||
图片预览



文档简介
第十八章 平行四边形
章末复习
【典例分析】
类型1 平行四边形的性质与判定
【例1】如图所示,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数.
【思路分析】(1)利用平行四边形对角相等证∠ADF=∠ABE,再利用平行四边形对边相等证上述两角的两边对应相等;(2)利用全等三角形的对应角相等,将其转化为求∠EAB+∠FAD的度数.
【规范解答】
【方法归纳】(1)平行四边形对边相等、对角相等的性质,常常为我们提供证明两个三角形全等边角相等的条件;(2)对于四边形的问题,我们常常把它转化为三角形的问题来解决,平行四边形也是如此.
类型2 特殊平行四边形的性质与判定
【例2】如图1,矩形ABCD中,O是对角线AC、BD的交点,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)求证:△BOE≌△DOF;
(2)如图2,当EF与AC满足什么关系时,以A、E、C、F为顶点的四边形是菱形?证明你的结论.
【思路分析】(1)由矩形对角线互相平分及平行线的内错角相等得到△BOE≌△DOF(AAS);(2)当EF⊥AC时,四边形AECF是菱形,可先证四边形AECF是平行四边形再推出它是菱形.
【规范解答】
【方法归纳】矩形、菱形、正方形都是特殊的平行四边形.它们的性质和判定主要从对边、对角、对角线三个方面进行总结,它们各自特有的性质可以为证明有关线段相等、角相等、直线平行与垂直等问题提供新的方法和思路,同时只要作出恰当的辅助线就可以将这些特殊的图形进一步分割成三角形,将它们与全等三角形、特殊三角形等图形紧密结合起来,就可以在丰富的知识背景下去探求问题的解答思路.
【综合练习】
1.下面的性质中,平行四边形不一定具有的是 ( )
A.对角互补 B.邻角互补 C.对角相等 D.对边相等
2.以长为5,4,7的三条线段中的两条为边,另一条为对角线画平行四边形,可以画出形状不同的平行四边形的个数是( )
A.1个 B.2个 C.3个 D.4个
3.下列命题是真命题的是( )
A.对角线相等的四边形是平行四边形
B.对角线互相平分且相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
4.下列命题正确的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线相互垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线相互垂直平分且相等的四边形是正方形
5.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
A.6 B.8
C.10 D.12
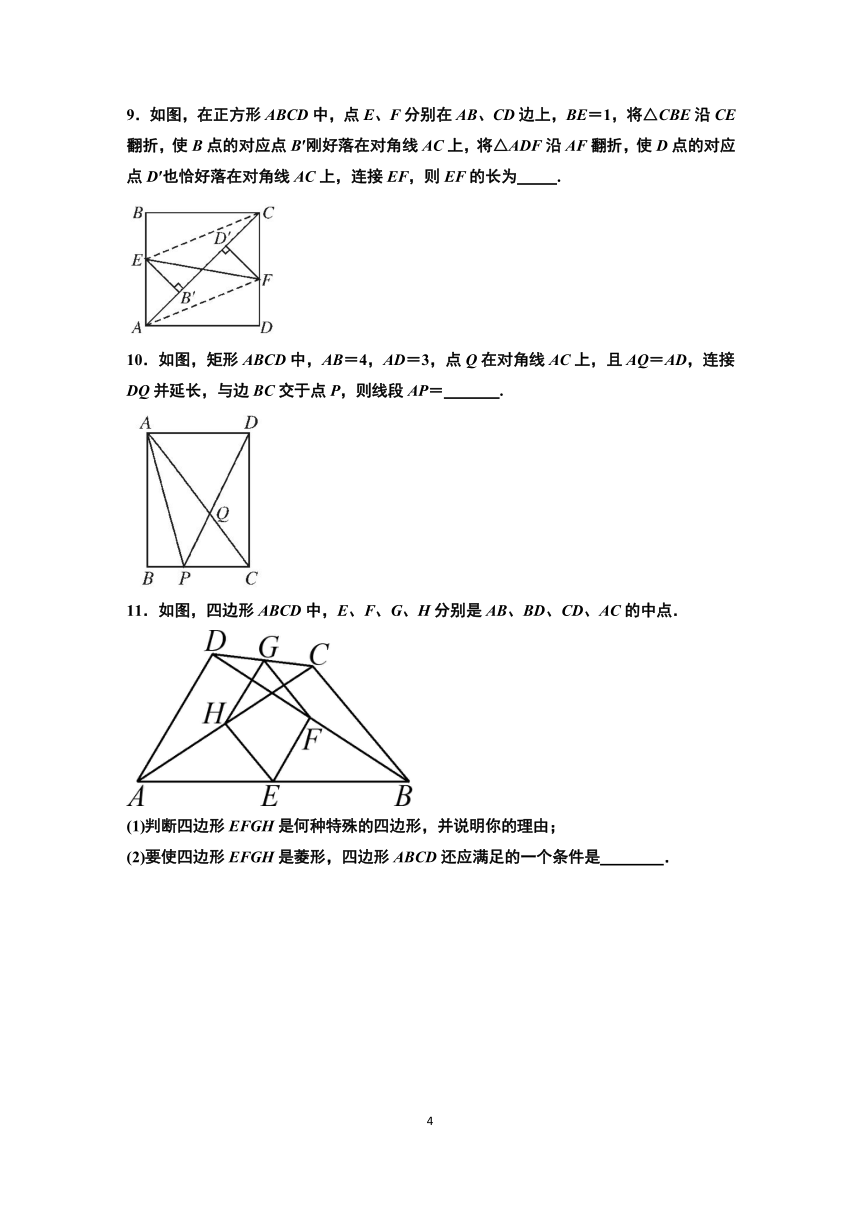
6.如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
A.AF=AE B.△ABE≌△AGF C.EF=2 D.AF=EF
7.如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
A.DE=DF B.EF=AB C.S△ABD=S△ACD D.AD平分∠BAC
8.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对角线的交点O分别作边AB、BC的垂线,交各边于点E、F、G、H,则四边形EFGH的周长为( )
A.3+ B.2+2 C.2+ D.1+2
9.如图,在正方形ABCD中,点E、F分别在AB、CD边上,BE=1,将△CBE沿CE翻折,使B点的对应点B′刚好落在对角线AC上,将△ADF沿AF翻折,使D点的对应点D′也恰好落在对角线AC上,连接EF,则EF的长为 .
10.如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
11.如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 .
12.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
13.正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连接DF、BF,如图.
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
14.如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE(1)求证:OM=ON;
(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.
1
参考答案
【典例分析】
类型1 平行四边形的性质与判定
【例1】如图所示,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数.
【思路分析】(1)利用平行四边形对角相等证∠ADF=∠ABE,再利用平行四边形对边相等证上述两角的两边对应相等;(2)利用全等三角形的对应角相等,将其转化为求∠EAB+∠FAD的度数.
【规范解答】(1)∵四边形ABCD是平行四边形,∴∠ADC=∠ABC,AD=BC=BE,DF=DC=AB.在△ABE和△FDA中,AB=FD,BE=DA,∠ABE=360°-∠ABC-∠EBC=360°-∠ADC-∠CDF=∠ADF,∴△ABE≌△FDA(SAS);
(2)由(1)得∠AEB=∠FAD,∴∠EBH=∠AEB+∠EAB=∠EAB+∠FAD=90°-∠BAD=90°-32°=58°,即∠EBH=58°.
【方法归纳】(1)平行四边形对边相等、对角相等的性质,常常为我们提供证明两个三角形全等边角相等的条件;(2)对于四边形的问题,我们常常把它转化为三角形的问题来解决,平行四边形也是如此.
类型2 特殊平行四边形的性质与判定
【例2】如图1,矩形ABCD中,O是对角线AC、BD的交点,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)求证:△BOE≌△DOF;
(2)如图2,当EF与AC满足什么关系时,以A、E、C、F为顶点的四边形是菱形?证明你的结论.
【思路分析】(1)由矩形对角线互相平分及平行线的内错角相等得到△BOE≌△DOF(AAS);(2)当EF⊥AC时,四边形AECF是菱形,可先证四边形AECF是平行四边形再推出它是菱形.
【规范解答】(1)∵四边形ABCD是矩形,∴OB=OD,AE∥CF,∴∠E=∠F,∠OBE=∠ODF,∴△BOE≌△DOF;
(2)当EF⊥AC时,四边形AECF是菱形.证明:∵四边形ABCD是矩形,∴OA=OC.又由(1)△BOE≌△DOF,得OE=OF,∴四边形AECF是平行四边形.又∵EF⊥AC,∴四边形AECF是菱形.
【方法归纳】矩形、菱形、正方形都是特殊的平行四边形.它们的性质和判定主要从对边、对角、对角线三个方面进行总结,它们各自特有的性质可以为证明有关线段相等、角相等、直线平行与垂直等问题提供新的方法和思路,同时只要作出恰当的辅助线就可以将这些特殊的图形进一步分割成三角形,将它们与全等三角形、特殊三角形等图形紧密结合起来,就可以在丰富的知识背景下去探求问题的解答思路.
【综合练习】
1.下面的性质中,平行四边形不一定具有的是 ( A )
A.对角互补 B.邻角互补 C.对角相等 D.对边相等
2.以长为5,4,7的三条线段中的两条为边,另一条为对角线画平行四边形,可以画出形状不同的平行四边形的个数是( C )
A.1个 B.2个 C.3个 D.4个
3.下列命题是真命题的是( B )
A.对角线相等的四边形是平行四边形
B.对角线互相平分且相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
4.下列命题正确的是( D )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线相互垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线相互垂直平分且相等的四边形是正方形
5.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( B )
A.6 B.8
C.10 D.12
6.如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( D )
A.AF=AE B.△ABE≌△AGF C.EF=2 D.AF=EF
7.如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( C )
A.DE=DF B.EF=AB C.S△ABD=S△ACD D.AD平分∠BAC
8.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对角线的交点O分别作边AB、BC的垂线,交各边于点E、F、G、H,则四边形EFGH的周长为( A )
A.3+ B.2+2 C.2+ D.1+2
9.如图,在正方形ABCD中,点E、F分别在AB、CD边上,BE=1,将△CBE沿CE翻折,使B点的对应点B′刚好落在对角线AC上,将△ADF沿AF翻折,使D点的对应点D′也恰好落在对角线AC上,连接EF,则EF的长为 .
【答案】
10.如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
【答案】
11.如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 .
解:(1)四边形EFGH是平行四边形.在△ACD中,∵G、H分别是CD、AC的中点,∴GH∥AD,GH=AD.在△ABD中,∵E、F分别是AB、BD的中点,∴EF∥AD,EF=AD,∴EF∥GH,EF=GH.∴四边形EFGH是平行四边形;
(2)AD=BC.
12.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
(1)证明:∵四边形ABCD为矩形,O是BD的中点,∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,∴∠OBE=∠ODF,在△BOE和△DOF中,,∴△BOE≌△DOF(ASA),∴EO=FO,∴四边形BEDF是平行四边形;
(2)解:当四边形BEDF是菱形时,BD⊥EF,设BE=x,则DE=x,AE=6-x,Rt△ADE中,DE2=AD2+AE2,∴x2=42+(6-x)2,解得:x=,∵BD==2,∴OB=BD=,∵BD⊥EF,∴EO==,∴EF=2EO=.
13.正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连接DF、BF,如图.
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
证明:(1)正方形ABCD和正方形AEFG中,∵GF=EF,AG=AE,AD=AB,∴DG=BE,又∵∠DGF=∠BEF=90°,∴△DGF≌△BEF(SAS),∴DF=BF; (2)反例图形如答图; (3)不唯一,如点F在正方形ABCD内或α<180°.
14.如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE(1)求证:OM=ON;
(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.
(1)证明:∵四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,
∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON;
(2)解:过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,
章末复习
【典例分析】
类型1 平行四边形的性质与判定
【例1】如图所示,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数.
【思路分析】(1)利用平行四边形对角相等证∠ADF=∠ABE,再利用平行四边形对边相等证上述两角的两边对应相等;(2)利用全等三角形的对应角相等,将其转化为求∠EAB+∠FAD的度数.
【规范解答】
【方法归纳】(1)平行四边形对边相等、对角相等的性质,常常为我们提供证明两个三角形全等边角相等的条件;(2)对于四边形的问题,我们常常把它转化为三角形的问题来解决,平行四边形也是如此.
类型2 特殊平行四边形的性质与判定
【例2】如图1,矩形ABCD中,O是对角线AC、BD的交点,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)求证:△BOE≌△DOF;
(2)如图2,当EF与AC满足什么关系时,以A、E、C、F为顶点的四边形是菱形?证明你的结论.
【思路分析】(1)由矩形对角线互相平分及平行线的内错角相等得到△BOE≌△DOF(AAS);(2)当EF⊥AC时,四边形AECF是菱形,可先证四边形AECF是平行四边形再推出它是菱形.
【规范解答】
【方法归纳】矩形、菱形、正方形都是特殊的平行四边形.它们的性质和判定主要从对边、对角、对角线三个方面进行总结,它们各自特有的性质可以为证明有关线段相等、角相等、直线平行与垂直等问题提供新的方法和思路,同时只要作出恰当的辅助线就可以将这些特殊的图形进一步分割成三角形,将它们与全等三角形、特殊三角形等图形紧密结合起来,就可以在丰富的知识背景下去探求问题的解答思路.
【综合练习】
1.下面的性质中,平行四边形不一定具有的是 ( )
A.对角互补 B.邻角互补 C.对角相等 D.对边相等
2.以长为5,4,7的三条线段中的两条为边,另一条为对角线画平行四边形,可以画出形状不同的平行四边形的个数是( )
A.1个 B.2个 C.3个 D.4个
3.下列命题是真命题的是( )
A.对角线相等的四边形是平行四边形
B.对角线互相平分且相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
4.下列命题正确的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线相互垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线相互垂直平分且相等的四边形是正方形
5.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
A.6 B.8
C.10 D.12
6.如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
A.AF=AE B.△ABE≌△AGF C.EF=2 D.AF=EF
7.如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
A.DE=DF B.EF=AB C.S△ABD=S△ACD D.AD平分∠BAC
8.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对角线的交点O分别作边AB、BC的垂线,交各边于点E、F、G、H,则四边形EFGH的周长为( )
A.3+ B.2+2 C.2+ D.1+2
9.如图,在正方形ABCD中,点E、F分别在AB、CD边上,BE=1,将△CBE沿CE翻折,使B点的对应点B′刚好落在对角线AC上,将△ADF沿AF翻折,使D点的对应点D′也恰好落在对角线AC上,连接EF,则EF的长为 .
10.如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
11.如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 .
12.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
13.正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连接DF、BF,如图.
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
14.如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE
(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.
1
参考答案
【典例分析】
类型1 平行四边形的性质与判定
【例1】如图所示,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数.
【思路分析】(1)利用平行四边形对角相等证∠ADF=∠ABE,再利用平行四边形对边相等证上述两角的两边对应相等;(2)利用全等三角形的对应角相等,将其转化为求∠EAB+∠FAD的度数.
【规范解答】(1)∵四边形ABCD是平行四边形,∴∠ADC=∠ABC,AD=BC=BE,DF=DC=AB.在△ABE和△FDA中,AB=FD,BE=DA,∠ABE=360°-∠ABC-∠EBC=360°-∠ADC-∠CDF=∠ADF,∴△ABE≌△FDA(SAS);
(2)由(1)得∠AEB=∠FAD,∴∠EBH=∠AEB+∠EAB=∠EAB+∠FAD=90°-∠BAD=90°-32°=58°,即∠EBH=58°.
【方法归纳】(1)平行四边形对边相等、对角相等的性质,常常为我们提供证明两个三角形全等边角相等的条件;(2)对于四边形的问题,我们常常把它转化为三角形的问题来解决,平行四边形也是如此.
类型2 特殊平行四边形的性质与判定
【例2】如图1,矩形ABCD中,O是对角线AC、BD的交点,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)求证:△BOE≌△DOF;
(2)如图2,当EF与AC满足什么关系时,以A、E、C、F为顶点的四边形是菱形?证明你的结论.
【思路分析】(1)由矩形对角线互相平分及平行线的内错角相等得到△BOE≌△DOF(AAS);(2)当EF⊥AC时,四边形AECF是菱形,可先证四边形AECF是平行四边形再推出它是菱形.
【规范解答】(1)∵四边形ABCD是矩形,∴OB=OD,AE∥CF,∴∠E=∠F,∠OBE=∠ODF,∴△BOE≌△DOF;
(2)当EF⊥AC时,四边形AECF是菱形.证明:∵四边形ABCD是矩形,∴OA=OC.又由(1)△BOE≌△DOF,得OE=OF,∴四边形AECF是平行四边形.又∵EF⊥AC,∴四边形AECF是菱形.
【方法归纳】矩形、菱形、正方形都是特殊的平行四边形.它们的性质和判定主要从对边、对角、对角线三个方面进行总结,它们各自特有的性质可以为证明有关线段相等、角相等、直线平行与垂直等问题提供新的方法和思路,同时只要作出恰当的辅助线就可以将这些特殊的图形进一步分割成三角形,将它们与全等三角形、特殊三角形等图形紧密结合起来,就可以在丰富的知识背景下去探求问题的解答思路.
【综合练习】
1.下面的性质中,平行四边形不一定具有的是 ( A )
A.对角互补 B.邻角互补 C.对角相等 D.对边相等
2.以长为5,4,7的三条线段中的两条为边,另一条为对角线画平行四边形,可以画出形状不同的平行四边形的个数是( C )
A.1个 B.2个 C.3个 D.4个
3.下列命题是真命题的是( B )
A.对角线相等的四边形是平行四边形
B.对角线互相平分且相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
4.下列命题正确的是( D )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线相互垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线相互垂直平分且相等的四边形是正方形
5.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( B )
A.6 B.8
C.10 D.12
6.如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( D )
A.AF=AE B.△ABE≌△AGF C.EF=2 D.AF=EF
7.如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( C )
A.DE=DF B.EF=AB C.S△ABD=S△ACD D.AD平分∠BAC
8.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对角线的交点O分别作边AB、BC的垂线,交各边于点E、F、G、H,则四边形EFGH的周长为( A )
A.3+ B.2+2 C.2+ D.1+2
9.如图,在正方形ABCD中,点E、F分别在AB、CD边上,BE=1,将△CBE沿CE翻折,使B点的对应点B′刚好落在对角线AC上,将△ADF沿AF翻折,使D点的对应点D′也恰好落在对角线AC上,连接EF,则EF的长为 .
【答案】
10.如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
【答案】
11.如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 .
解:(1)四边形EFGH是平行四边形.在△ACD中,∵G、H分别是CD、AC的中点,∴GH∥AD,GH=AD.在△ABD中,∵E、F分别是AB、BD的中点,∴EF∥AD,EF=AD,∴EF∥GH,EF=GH.∴四边形EFGH是平行四边形;
(2)AD=BC.
12.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
(1)证明:∵四边形ABCD为矩形,O是BD的中点,∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,∴∠OBE=∠ODF,在△BOE和△DOF中,,∴△BOE≌△DOF(ASA),∴EO=FO,∴四边形BEDF是平行四边形;
(2)解:当四边形BEDF是菱形时,BD⊥EF,设BE=x,则DE=x,AE=6-x,Rt△ADE中,DE2=AD2+AE2,∴x2=42+(6-x)2,解得:x=,∵BD==2,∴OB=BD=,∵BD⊥EF,∴EO==,∴EF=2EO=.
13.正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连接DF、BF,如图.
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
证明:(1)正方形ABCD和正方形AEFG中,∵GF=EF,AG=AE,AD=AB,∴DG=BE,又∵∠DGF=∠BEF=90°,∴△DGF≌△BEF(SAS),∴DF=BF; (2)反例图形如答图; (3)不唯一,如点F在正方形ABCD内或α<180°.
14.如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE
(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.
(1)证明:∵四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,
∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON;
(2)解:过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,
