人教版七年级下册数学5.1相交线成果展示(含答案)
文档属性
| 名称 | 人教版七年级下册数学5.1相交线成果展示(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 411.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-15 11:50:00 | ||
图片预览

文档简介
人教版七年级下册数学5.1相交线成果展示(含答案)
一、选择题
1.同一平面内互不重合的3条直线的交点的个数是( )
A.可能是0,1,2 B.可能是0,2,3
C.可能是0,1,2或3 D.可能是1,可能是3
2.下列叙述中,正确的是( )
A.在同一平面内,两条直线的位置关系有三种,分别是相交、垂直、平行
B.不相交的两条直线叫做平行线
C.长方形的一组对边是平行的
D.我们知道,对顶角是相等的;反之,相等的角就是对顶角
3.下面四个图形中,与是对顶角的图形是( )
A. B.C. D.
4.如果两条直线被第三条直线所截,那么( )
A.同位角相等 B.内错角相等
C.同旁内角互补 D.对顶角相等
5.在平面直角坐标系中,点A的坐标是,它到x轴的距离为( )
A.3 B. C.2 D.
6.如下左图所示,下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误的是( )
A.① B.② C.③ D.④
7.如上右图所示,点P在的平分线上,且点P到边的距离等于2,点Q是边上的任意一点,则的长不可能是( )
A.1 B.2 C.3 D.4
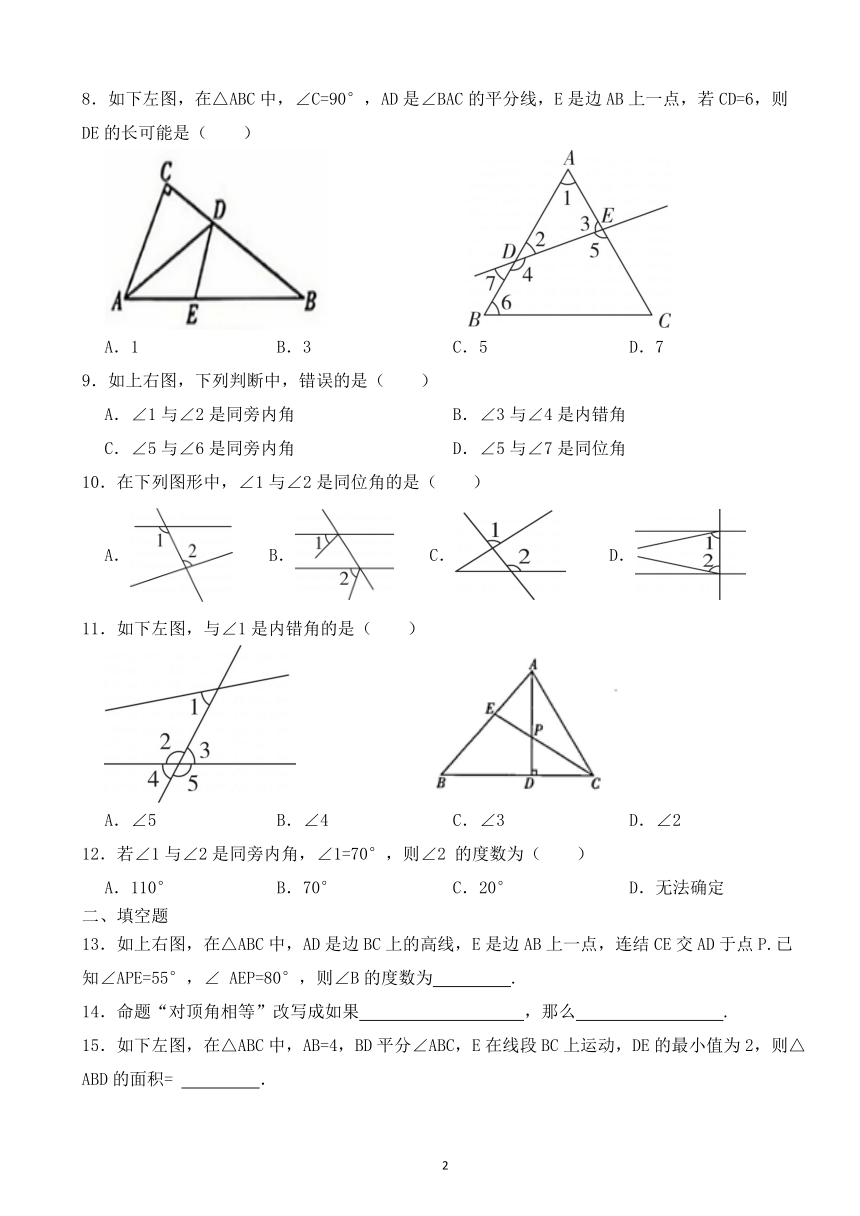
8.如下左图,在△ABC中,∠C=90°,AD是∠BAC的平分线,E是边AB上一点,若CD=6,则DE的长可能是( )
A.1 B.3 C.5 D.7
9.如上右图,下列判断中,错误的是( )
A.∠1与∠2是同旁内角 B.∠3与∠4是内错角
C.∠5与∠6是同旁内角 D.∠5与∠7是同位角
10.在下列图形中,∠1与∠2是同位角的是( )
A. B. C. D.
11.如下左图,与∠1是内错角的是( )
A.∠5 B.∠4 C.∠3 D.∠2
12.若∠1与∠2是同旁内角,∠1=70°,则∠2 的度数为( )
A.110° B.70° C.20° D.无法确定
二、填空题
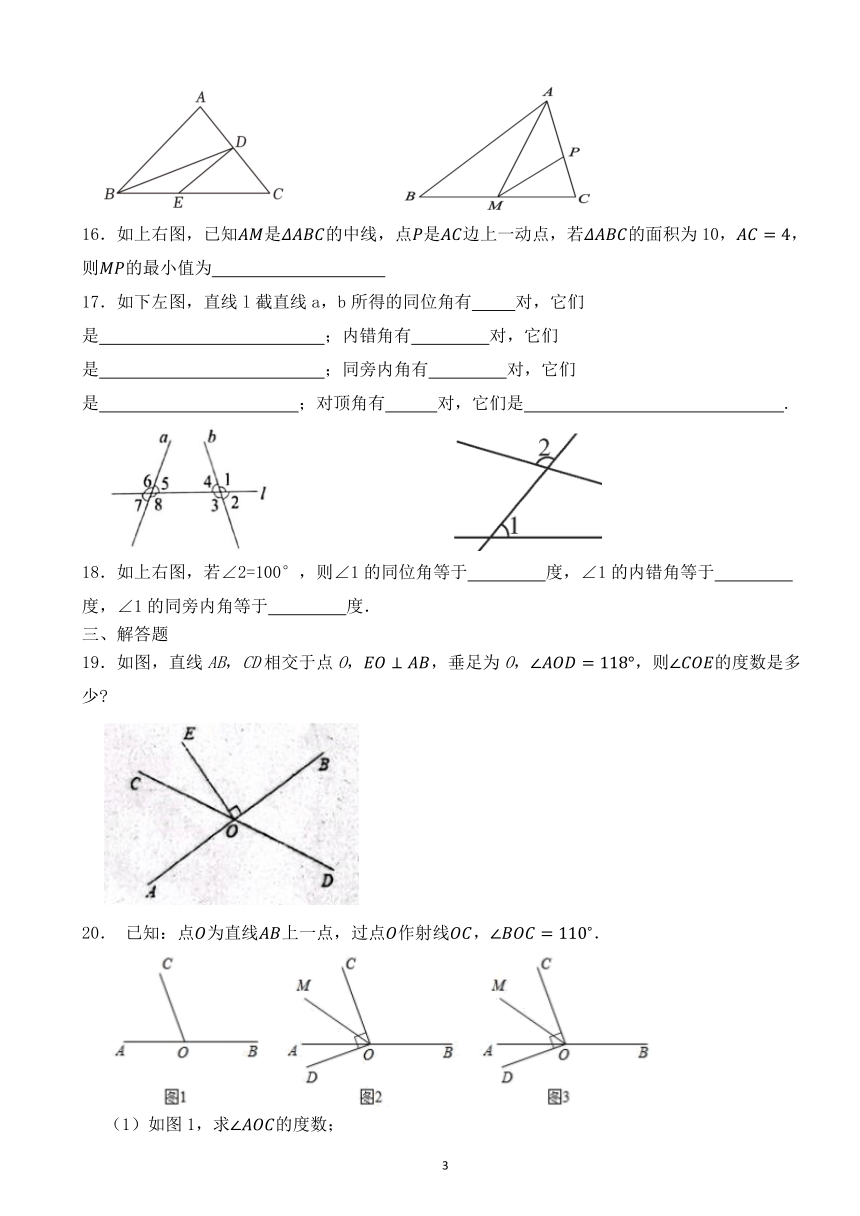
13.如上右图,在△ABC中,AD是边BC上的高线,E是边AB上一点,连结CE交AD于点P.已知∠APE=55°,∠ AEP=80°,则∠B的度数为 .
14.命题“对顶角相等”改写成如果 ,那么 .
15.如下左图,在△ABC中,AB=4,BD平分∠ABC,E在线段BC上运动,DE的最小值为2,则△ABD的面积= .
16.如上右图,已知是的中线,点是边上一动点,若的面积为10,,则的最小值为
17.如下左图,直线l截直线a,b所得的同位角有 对,它们是 ;内错角有 对,它们是 ;同旁内角有 对,它们是 ;对顶角有 对,它们是 .
18.如上右图,若∠2=100°,则∠1的同位角等于 度,∠1的内错角等于 度,∠1的同旁内角等于 度.
三、解答题
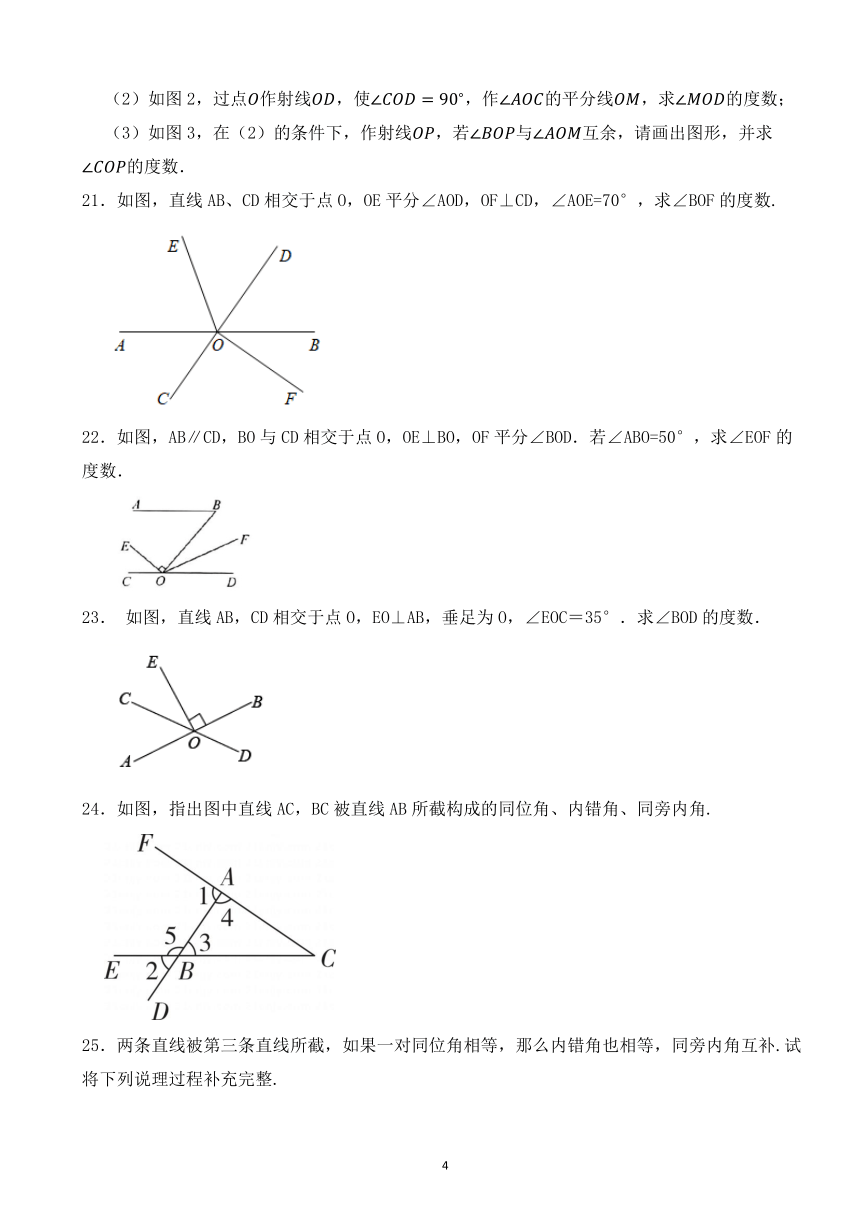
19.如图,直线AB,CD相交于点O,,垂足为O,,则的度数是多少
20. 已知:点为直线上一点,过点作射线,.
(1)如图1,求的度数;
(2)如图2,过点作射线,使,作的平分线,求的度数;
(3)如图3,在(2)的条件下,作射线,若与互余,请画出图形,并求的度数.
21.如图,直线AB、CD相交于点O,OE平分∠AOD,OF⊥CD,∠AOE=70°,求∠BOF的度数.
22.如图,AB∥CD,BO与CD相交于点O,OE⊥BO,OF平分∠BOD.若∠ABO=50°,求∠EOF的度数.
23. 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°.求∠BOD的度数.
24.如图,指出图中直线AC,BC被直线AB所截构成的同位角、内错角、同旁内角.
25.两条直线被第三条直线所截,如果一对同位角相等,那么内错角也相等,同旁内角互补.试将下列说理过程补充完整.
解:如图,设∠1=∠3.
∵∠1+∠2= °(平角的定义),
∴∠3+ =180°.
又∵∠4+∠3= °(平角的定义),
∴∠2=∠4( ).
答案
一、1.C 2.C 3.C 4.D 5.C 6.C 7.A 8.D 9.C 10.C 11.C 12.D
二、13.45°
14.两个角是对顶角;这两个角相等
15.4
16.2.5或或
17.4;∠1与∠5,∠4与∠6,∠2与∠8,∠3与∠7;2;∠4与∠8,∠3与∠5;2;∠4与∠5,∠3与∠8;4;∠1与∠3,∠4与∠2,∠6与∠8,∠5与∠7
18.80;80;100
三、19.解:∵,∴,
∵,∴.
∴,
∴.
20.(1)解: ∵,,
∴.
(2)解:由(1)知,
∵OM平分∠AOC,
∴,
又∵,
∴.
(3)解:由(2)知,
∵∠BOP与∠AOM互余,
∴,
∴,
①当射线OP在∠BOC内部时,
,
②当射线OP在∠BOC外部时,
,
综上所述,∠COP的度数为55°或165°.
21.解:∵OE平分且,
∴,
∵A、O、B三点共线,
∴,
∵,
∴,
∴
22.解:∵AB∥CD, ∠ABO=50°,
∴∠BOD=∠ABO=50°,
∵OF平分∠BOD,
∴∠BOF=∠BOD=25°,
∵EO⊥BO,
∴∠BOE=90°,
∴∠EOF=∠BOE+∠BOF=115°.
23.解:∵EO⊥AB,
∴∠AOE=90°,
∵∠EOC=35°,
∴∠AOC=∠AOE-∠EOC=55°,
∴∠BOD=∠AOC=55°
24.解:∠1与∠2,∠4与∠DBC是同位角;
∠1与∠3,∠4与∠5是内错角;
∠3与∠4,∠1与∠5是同旁内角
25.解:如图,设∠1=∠3.
∵∠1+∠2=180°(平角的定义),
∴∠3+∠2=180°.
又∵∠4+∠3=180°(平角的定义),
∴∠2=∠4(同角的补角相等).
一、选择题
1.同一平面内互不重合的3条直线的交点的个数是( )
A.可能是0,1,2 B.可能是0,2,3
C.可能是0,1,2或3 D.可能是1,可能是3
2.下列叙述中,正确的是( )
A.在同一平面内,两条直线的位置关系有三种,分别是相交、垂直、平行
B.不相交的两条直线叫做平行线
C.长方形的一组对边是平行的
D.我们知道,对顶角是相等的;反之,相等的角就是对顶角
3.下面四个图形中,与是对顶角的图形是( )
A. B.C. D.
4.如果两条直线被第三条直线所截,那么( )
A.同位角相等 B.内错角相等
C.同旁内角互补 D.对顶角相等
5.在平面直角坐标系中,点A的坐标是,它到x轴的距离为( )
A.3 B. C.2 D.
6.如下左图所示,下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误的是( )
A.① B.② C.③ D.④
7.如上右图所示,点P在的平分线上,且点P到边的距离等于2,点Q是边上的任意一点,则的长不可能是( )
A.1 B.2 C.3 D.4
8.如下左图,在△ABC中,∠C=90°,AD是∠BAC的平分线,E是边AB上一点,若CD=6,则DE的长可能是( )
A.1 B.3 C.5 D.7
9.如上右图,下列判断中,错误的是( )
A.∠1与∠2是同旁内角 B.∠3与∠4是内错角
C.∠5与∠6是同旁内角 D.∠5与∠7是同位角
10.在下列图形中,∠1与∠2是同位角的是( )
A. B. C. D.
11.如下左图,与∠1是内错角的是( )
A.∠5 B.∠4 C.∠3 D.∠2
12.若∠1与∠2是同旁内角,∠1=70°,则∠2 的度数为( )
A.110° B.70° C.20° D.无法确定
二、填空题
13.如上右图,在△ABC中,AD是边BC上的高线,E是边AB上一点,连结CE交AD于点P.已知∠APE=55°,∠ AEP=80°,则∠B的度数为 .
14.命题“对顶角相等”改写成如果 ,那么 .
15.如下左图,在△ABC中,AB=4,BD平分∠ABC,E在线段BC上运动,DE的最小值为2,则△ABD的面积= .
16.如上右图,已知是的中线,点是边上一动点,若的面积为10,,则的最小值为
17.如下左图,直线l截直线a,b所得的同位角有 对,它们是 ;内错角有 对,它们是 ;同旁内角有 对,它们是 ;对顶角有 对,它们是 .
18.如上右图,若∠2=100°,则∠1的同位角等于 度,∠1的内错角等于 度,∠1的同旁内角等于 度.
三、解答题
19.如图,直线AB,CD相交于点O,,垂足为O,,则的度数是多少
20. 已知:点为直线上一点,过点作射线,.
(1)如图1,求的度数;
(2)如图2,过点作射线,使,作的平分线,求的度数;
(3)如图3,在(2)的条件下,作射线,若与互余,请画出图形,并求的度数.
21.如图,直线AB、CD相交于点O,OE平分∠AOD,OF⊥CD,∠AOE=70°,求∠BOF的度数.
22.如图,AB∥CD,BO与CD相交于点O,OE⊥BO,OF平分∠BOD.若∠ABO=50°,求∠EOF的度数.
23. 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°.求∠BOD的度数.
24.如图,指出图中直线AC,BC被直线AB所截构成的同位角、内错角、同旁内角.
25.两条直线被第三条直线所截,如果一对同位角相等,那么内错角也相等,同旁内角互补.试将下列说理过程补充完整.
解:如图,设∠1=∠3.
∵∠1+∠2= °(平角的定义),
∴∠3+ =180°.
又∵∠4+∠3= °(平角的定义),
∴∠2=∠4( ).
答案
一、1.C 2.C 3.C 4.D 5.C 6.C 7.A 8.D 9.C 10.C 11.C 12.D
二、13.45°
14.两个角是对顶角;这两个角相等
15.4
16.2.5或或
17.4;∠1与∠5,∠4与∠6,∠2与∠8,∠3与∠7;2;∠4与∠8,∠3与∠5;2;∠4与∠5,∠3与∠8;4;∠1与∠3,∠4与∠2,∠6与∠8,∠5与∠7
18.80;80;100
三、19.解:∵,∴,
∵,∴.
∴,
∴.
20.(1)解: ∵,,
∴.
(2)解:由(1)知,
∵OM平分∠AOC,
∴,
又∵,
∴.
(3)解:由(2)知,
∵∠BOP与∠AOM互余,
∴,
∴,
①当射线OP在∠BOC内部时,
,
②当射线OP在∠BOC外部时,
,
综上所述,∠COP的度数为55°或165°.
21.解:∵OE平分且,
∴,
∵A、O、B三点共线,
∴,
∵,
∴,
∴
22.解:∵AB∥CD, ∠ABO=50°,
∴∠BOD=∠ABO=50°,
∵OF平分∠BOD,
∴∠BOF=∠BOD=25°,
∵EO⊥BO,
∴∠BOE=90°,
∴∠EOF=∠BOE+∠BOF=115°.
23.解:∵EO⊥AB,
∴∠AOE=90°,
∵∠EOC=35°,
∴∠AOC=∠AOE-∠EOC=55°,
∴∠BOD=∠AOC=55°
24.解:∠1与∠2,∠4与∠DBC是同位角;
∠1与∠3,∠4与∠5是内错角;
∠3与∠4,∠1与∠5是同旁内角
25.解:如图,设∠1=∠3.
∵∠1+∠2=180°(平角的定义),
∴∠3+∠2=180°.
又∵∠4+∠3=180°(平角的定义),
∴∠2=∠4(同角的补角相等).
