第十八章 平行四边形 测试卷(含答案)
文档属性
| 名称 | 第十八章 平行四边形 测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 209.2KB | ||
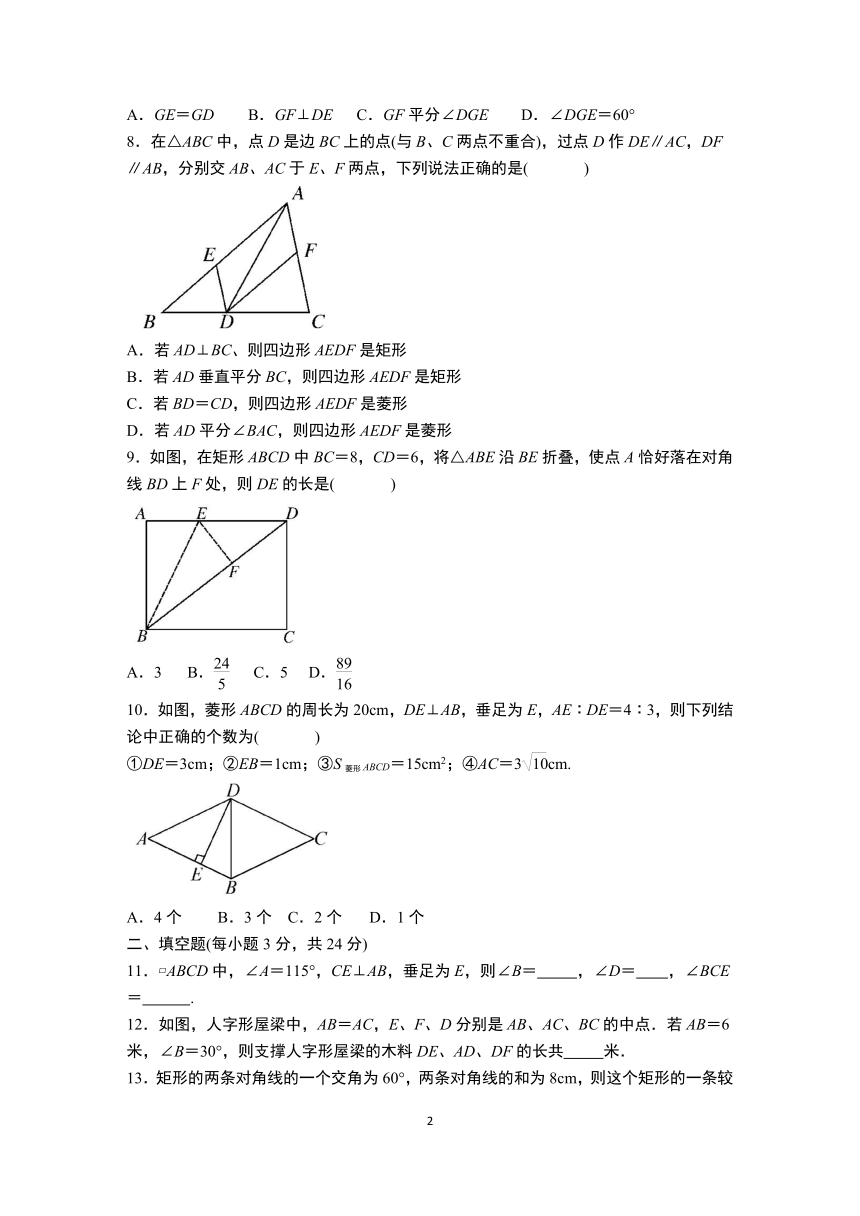
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-15 00:00:00 | ||
图片预览


文档简介
第十八章 平行四边形 测试卷
一、选择题(每小题3分,共30分)
1.如图,在 ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC于点E,则CE的长等于( )
A.8cm B.6cm C.4cm D.2cm
2.一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是( )
A.88°,108°,88° B.88°,104°,108° C.88°,92°,92° D.88°,92°,88°
3.正方形的一条对角线长为4,则这个正方形的面积是( )
A.8 B.4 C.8 D.16
4.下列结论中,矩形具有而菱形不一定具有的性质是( )
A.内角和为360° B.对角线互相平分 C.对角线相等 D.对角线互相垂直
5.如图, ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO、AB于点M、N;②以点O为圆心,以AM长为半径作弧,交OC于点M′;③以点M′为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N′;④过点N′作射线ON′交BC于点E.若AB=8,则线段OE的长为( )
A.2 B.4 C. D.6
6.已知直线a∥b,点M到直线a的距离是6cm,到直线b的距离是3cm,那么直线a和直线b之间的距离是( )
A.3cm B.9cm C.3cm或9cm D.6cm
7.如图所示,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,则下列结论中错误的是( )
A.GE=GD B.GF⊥DE C.GF平分∠DGE D.∠DGE=60°
8.在△ABC中,点D是边BC上的点(与B、C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB、AC于E、F两点,下列说法正确的是( )
A.若AD⊥BC、则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
9.如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
A.3 B. C.5 D.
10.如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,AE∶DE=4∶3,则下列结论中正确的个数为( )
①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④AC=3cm.
A.4个 B.3个 C.2个 D.1个
二、填空题(每小题3分,共24分)
11. ABCD中,∠A=115°,CE⊥AB,垂足为E,则∠B= ,∠D= ,∠BCE= .
12.如图,人字形屋梁中,AB=AC,E、F、D分别是AB、AC、BC的中点.若AB=6米,∠B=30°,则支撑人字形屋梁的木料DE、AD、DF的长共 米.
13.矩形的两条对角线的一个交角为60°,两条对角线的和为8cm,则这个矩形的一条较短边为 .
14.如图,四边形ABCD的对角线互相垂直,且OB=OD,请你添加一个适当的条件 ,使四边形ABCD成为菱形(只需添加一个即可).
15.如图,在等腰三角形ABC中,AB=AC=10,BC=12,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是 .
16.菱形的周长为20cm,两个相邻的内角的度数之比为1∶2,则较长的对角线的长度是 cm.
17.在平行四边形ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB= .
18.如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA、EB为折痕将两个角(∠D、∠C)向内折叠,点C、D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为 .
三、解答题(共66分)
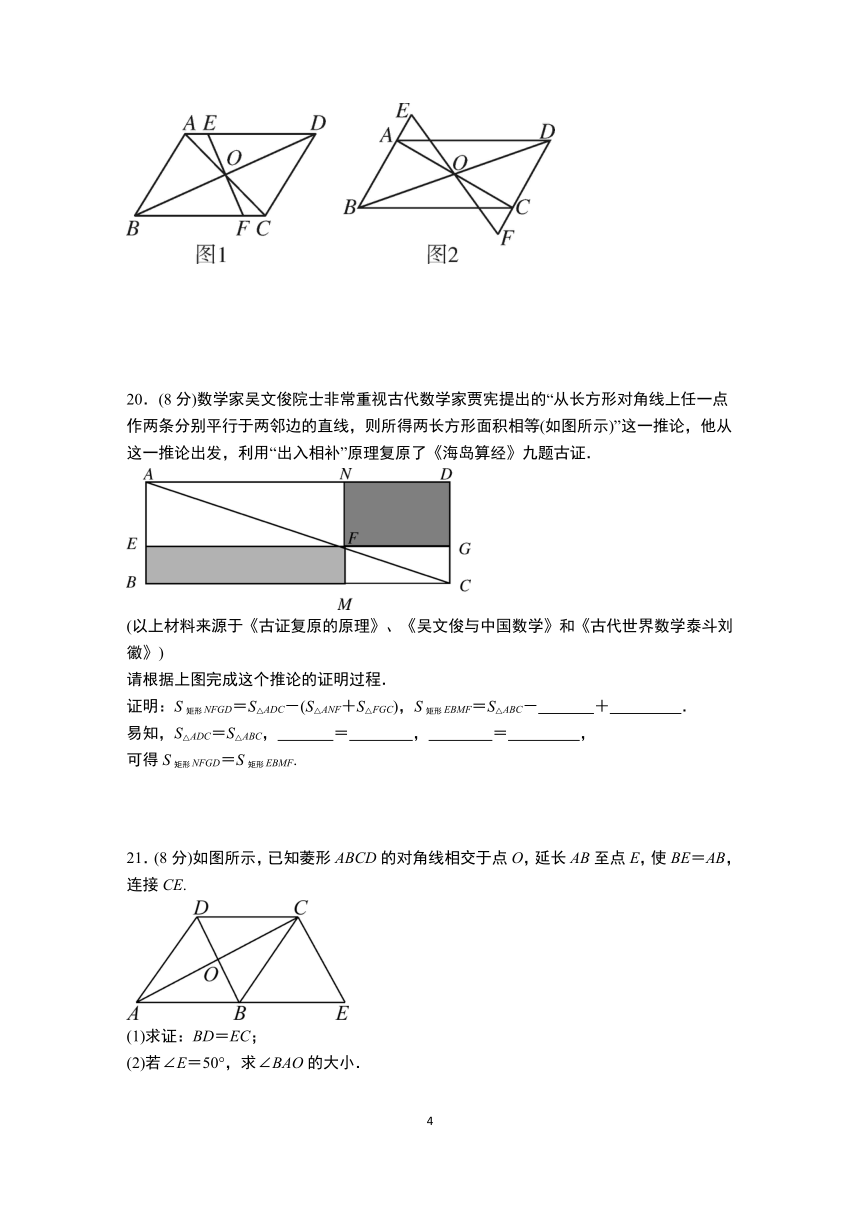
19.(8分)如图1, ABCD的对角线AC、BD相交于点O,过点O作直线EF分别交AD、BC于点E、F.
(1)求证:OE=OF;
(2)如图2,若过点O的直线与BA、DC的延长线分别交于E、F,能得到(1)中的结论吗?由此你能得到什么样的一般性的结论?
20.(8分)数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC- + .
易知,S△ADC=S△ABC, = , = ,
可得S矩形NFGD=S矩形EBMF.
21.(8分)如图所示,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
23.(10分)已知:如图, ABCD的对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
24.(10分)已知:如图,在菱形ABCD中,点E、O、F分别是AB、AC、AD的中点,连接CE、CF、OE、OF.
(1)证明:△BCE≌△DCF;
(2)当AB与AD满足什么条件时,四边形AEOF是正方形?请说明理由.
25.(12分)问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】
如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】
如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(-1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:=1.41,=1.73).
1
参考答案
1-10
CDACB CDDCA
11. 65° 65° 25°
12. 9
13. 2cm
14. 答案不唯一,如OA=OC或AD=BC或AD∥BC或AB=BC
15. 10cm或2cm或4cm
16. 5
17. 8或3
18.
19. (1)证明:∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC,∴∠EAO=∠FCO,∠AEO=∠CFO,∴△AEO≌△CFO(AAS),∴OE=OF;
(2)解:能得到(1)中的结论.∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC,∴∠EAO=∠FCO,∠AEO=∠CFO,∴△AEO≌△CFO(AAS),∴OE=OF.一般性的结论是:过平行四边形的对角线的交点O作一条直线与平行四边形相对的边或延长线相交于E、F两点,则OE=OF.
20. (S△AEF S△CFM) S△ANF S△AEF S△FGC S△CFM
21. (1)证明:∵菱形ABCD,∴AB=CD,AB∥CD,又∵BE=AB,∴BE=CD,BE∥CD,∴四边形BECD是平行四边形,∴BD=EC;
(2)解:∵平行四边形BECD,∴BD∥CE,∴∠ABO=∠E=50°,又∵菱形ABCD,∴AC⊥BD,∴∠BAO=90°-∠ABO=40°.
22. (1)证明:∵E是AC的中点,∴EC=AC,∵DB=AC,∴DB=EC,又∵DB∥EC,∴四边形DBCE是平行四边形.∴BC=DE.
(2)解:添加AB=BC.理由:∵DB∥AE,DB=AE,∴四边形DBEA是平行四边形.∵BC=DE,AB=BC,∴AB=DE.∴ ADBE是矩形.
23. (1)证明:∵四边形ABCD是平行四边形,∴DC∥BF,DC=AB,∴∠GAF=∠GDC,∠GFA=∠GCD.∵点G为AD的中点,∴AG=DG,在△GAF和△GDC中,,∴△GAF≌△GDC(AAS),∴AF=DC,∴AB=AF;
(2)解:四边形ACDF是矩形.证明如下:∵AB=AF,∴点A是BF的中点,∵点G是AD的中点,AG=AB,∴BF=AD.∵在 ABCD中,AD=BC,∴BF=BC,∴△BCF为等腰三角形,∴∠BFC=∠BCF.∵BF∥DC,∴∠BFC=∠FCD,∴∠BCF=∠FCD=∠BCD=60°,∴△BCF为等边三角形,∴FC=BC,由(1)知AF=DC,AF∥DC,∴四边形ACDF为平行四边形.∵FC=BC=AD,∴四边形ACDF是矩形.
24. (1)证明:∵四边形ABCD为菱形,∴AB=BC=CD=DA,∠B=∠D.又E、F分别是AB、AD的中点,∴BE=DF,∴△BCE≌△DCF(SAS);
(2)解:若AB⊥AD,则四边形AEOF为正方形,理由如下:∵E、O分别是AB、AC的中点,∴EO∥BC,又BC∥AD,∴OE∥AD,即OE∥AF,同理可证:OF∥AE,所以四边形AEOF为平行四边形,由(1)可得AE=AF,所以平行四边形AEOF为菱形,因为AD⊥AB,所以∠BAD=90°,所以菱形AEOF为正方形.
25. 【发现证明】证明:如图(1),∵△ADG≌△ABE,∴AG=AE,∠DAG=∠BAE,DG=BE,又∵∠EAF=45°,即∠DAF+∠BAE=∠EAF=45°,∴∠GAF=∠FAE,在△GAF和△FAE中,,∴△AFG≌△AFE(SAS).∴GF=EF.又∵DG=BE,∴GF=BE+DF,∴BE+DF=EF.
【类比引申】解:∠BAD=2∠EAF.
【探究应用】解:如图,延长BA与CD交于点G,连接AF.∵∠BAD=150°,∠ADC=120°,∴∠DAG=30°,∠ADG=60°,∴∠AGD=90°,∵AD=AB=80,∴AG=40,DG=40,∵DF=40(-1),∴GF=40,∴AG=GF,∴∠GAF=45°,∴∠DAF=15°,∵AE⊥AD,∴∠EAF=90°-15°=75°=∠BAD,又∵AB=AD,由(2)得,EF=BE+DF=80+40(-1)≈109(米),即这条道路EF的长约为109米.
一、选择题(每小题3分,共30分)
1.如图,在 ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC于点E,则CE的长等于( )
A.8cm B.6cm C.4cm D.2cm
2.一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是( )
A.88°,108°,88° B.88°,104°,108° C.88°,92°,92° D.88°,92°,88°
3.正方形的一条对角线长为4,则这个正方形的面积是( )
A.8 B.4 C.8 D.16
4.下列结论中,矩形具有而菱形不一定具有的性质是( )
A.内角和为360° B.对角线互相平分 C.对角线相等 D.对角线互相垂直
5.如图, ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO、AB于点M、N;②以点O为圆心,以AM长为半径作弧,交OC于点M′;③以点M′为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N′;④过点N′作射线ON′交BC于点E.若AB=8,则线段OE的长为( )
A.2 B.4 C. D.6
6.已知直线a∥b,点M到直线a的距离是6cm,到直线b的距离是3cm,那么直线a和直线b之间的距离是( )
A.3cm B.9cm C.3cm或9cm D.6cm
7.如图所示,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,则下列结论中错误的是( )
A.GE=GD B.GF⊥DE C.GF平分∠DGE D.∠DGE=60°
8.在△ABC中,点D是边BC上的点(与B、C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB、AC于E、F两点,下列说法正确的是( )
A.若AD⊥BC、则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
9.如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
A.3 B. C.5 D.
10.如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,AE∶DE=4∶3,则下列结论中正确的个数为( )
①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④AC=3cm.
A.4个 B.3个 C.2个 D.1个
二、填空题(每小题3分,共24分)
11. ABCD中,∠A=115°,CE⊥AB,垂足为E,则∠B= ,∠D= ,∠BCE= .
12.如图,人字形屋梁中,AB=AC,E、F、D分别是AB、AC、BC的中点.若AB=6米,∠B=30°,则支撑人字形屋梁的木料DE、AD、DF的长共 米.
13.矩形的两条对角线的一个交角为60°,两条对角线的和为8cm,则这个矩形的一条较短边为 .
14.如图,四边形ABCD的对角线互相垂直,且OB=OD,请你添加一个适当的条件 ,使四边形ABCD成为菱形(只需添加一个即可).
15.如图,在等腰三角形ABC中,AB=AC=10,BC=12,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是 .
16.菱形的周长为20cm,两个相邻的内角的度数之比为1∶2,则较长的对角线的长度是 cm.
17.在平行四边形ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB= .
18.如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA、EB为折痕将两个角(∠D、∠C)向内折叠,点C、D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为 .
三、解答题(共66分)
19.(8分)如图1, ABCD的对角线AC、BD相交于点O,过点O作直线EF分别交AD、BC于点E、F.
(1)求证:OE=OF;
(2)如图2,若过点O的直线与BA、DC的延长线分别交于E、F,能得到(1)中的结论吗?由此你能得到什么样的一般性的结论?
20.(8分)数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC- + .
易知,S△ADC=S△ABC, = , = ,
可得S矩形NFGD=S矩形EBMF.
21.(8分)如图所示,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
23.(10分)已知:如图, ABCD的对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
24.(10分)已知:如图,在菱形ABCD中,点E、O、F分别是AB、AC、AD的中点,连接CE、CF、OE、OF.
(1)证明:△BCE≌△DCF;
(2)当AB与AD满足什么条件时,四边形AEOF是正方形?请说明理由.
25.(12分)问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】
如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】
如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(-1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:=1.41,=1.73).
1
参考答案
1-10
CDACB CDDCA
11. 65° 65° 25°
12. 9
13. 2cm
14. 答案不唯一,如OA=OC或AD=BC或AD∥BC或AB=BC
15. 10cm或2cm或4cm
16. 5
17. 8或3
18.
19. (1)证明:∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC,∴∠EAO=∠FCO,∠AEO=∠CFO,∴△AEO≌△CFO(AAS),∴OE=OF;
(2)解:能得到(1)中的结论.∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC,∴∠EAO=∠FCO,∠AEO=∠CFO,∴△AEO≌△CFO(AAS),∴OE=OF.一般性的结论是:过平行四边形的对角线的交点O作一条直线与平行四边形相对的边或延长线相交于E、F两点,则OE=OF.
20. (S△AEF S△CFM) S△ANF S△AEF S△FGC S△CFM
21. (1)证明:∵菱形ABCD,∴AB=CD,AB∥CD,又∵BE=AB,∴BE=CD,BE∥CD,∴四边形BECD是平行四边形,∴BD=EC;
(2)解:∵平行四边形BECD,∴BD∥CE,∴∠ABO=∠E=50°,又∵菱形ABCD,∴AC⊥BD,∴∠BAO=90°-∠ABO=40°.
22. (1)证明:∵E是AC的中点,∴EC=AC,∵DB=AC,∴DB=EC,又∵DB∥EC,∴四边形DBCE是平行四边形.∴BC=DE.
(2)解:添加AB=BC.理由:∵DB∥AE,DB=AE,∴四边形DBEA是平行四边形.∵BC=DE,AB=BC,∴AB=DE.∴ ADBE是矩形.
23. (1)证明:∵四边形ABCD是平行四边形,∴DC∥BF,DC=AB,∴∠GAF=∠GDC,∠GFA=∠GCD.∵点G为AD的中点,∴AG=DG,在△GAF和△GDC中,,∴△GAF≌△GDC(AAS),∴AF=DC,∴AB=AF;
(2)解:四边形ACDF是矩形.证明如下:∵AB=AF,∴点A是BF的中点,∵点G是AD的中点,AG=AB,∴BF=AD.∵在 ABCD中,AD=BC,∴BF=BC,∴△BCF为等腰三角形,∴∠BFC=∠BCF.∵BF∥DC,∴∠BFC=∠FCD,∴∠BCF=∠FCD=∠BCD=60°,∴△BCF为等边三角形,∴FC=BC,由(1)知AF=DC,AF∥DC,∴四边形ACDF为平行四边形.∵FC=BC=AD,∴四边形ACDF是矩形.
24. (1)证明:∵四边形ABCD为菱形,∴AB=BC=CD=DA,∠B=∠D.又E、F分别是AB、AD的中点,∴BE=DF,∴△BCE≌△DCF(SAS);
(2)解:若AB⊥AD,则四边形AEOF为正方形,理由如下:∵E、O分别是AB、AC的中点,∴EO∥BC,又BC∥AD,∴OE∥AD,即OE∥AF,同理可证:OF∥AE,所以四边形AEOF为平行四边形,由(1)可得AE=AF,所以平行四边形AEOF为菱形,因为AD⊥AB,所以∠BAD=90°,所以菱形AEOF为正方形.
25. 【发现证明】证明:如图(1),∵△ADG≌△ABE,∴AG=AE,∠DAG=∠BAE,DG=BE,又∵∠EAF=45°,即∠DAF+∠BAE=∠EAF=45°,∴∠GAF=∠FAE,在△GAF和△FAE中,,∴△AFG≌△AFE(SAS).∴GF=EF.又∵DG=BE,∴GF=BE+DF,∴BE+DF=EF.
【类比引申】解:∠BAD=2∠EAF.
【探究应用】解:如图,延长BA与CD交于点G,连接AF.∵∠BAD=150°,∠ADC=120°,∴∠DAG=30°,∠ADG=60°,∴∠AGD=90°,∵AD=AB=80,∴AG=40,DG=40,∵DF=40(-1),∴GF=40,∴AG=GF,∴∠GAF=45°,∴∠DAF=15°,∵AE⊥AD,∴∠EAF=90°-15°=75°=∠BAD,又∵AB=AD,由(2)得,EF=BE+DF=80+40(-1)≈109(米),即这条道路EF的长约为109米.
