不等式的性质
图片预览






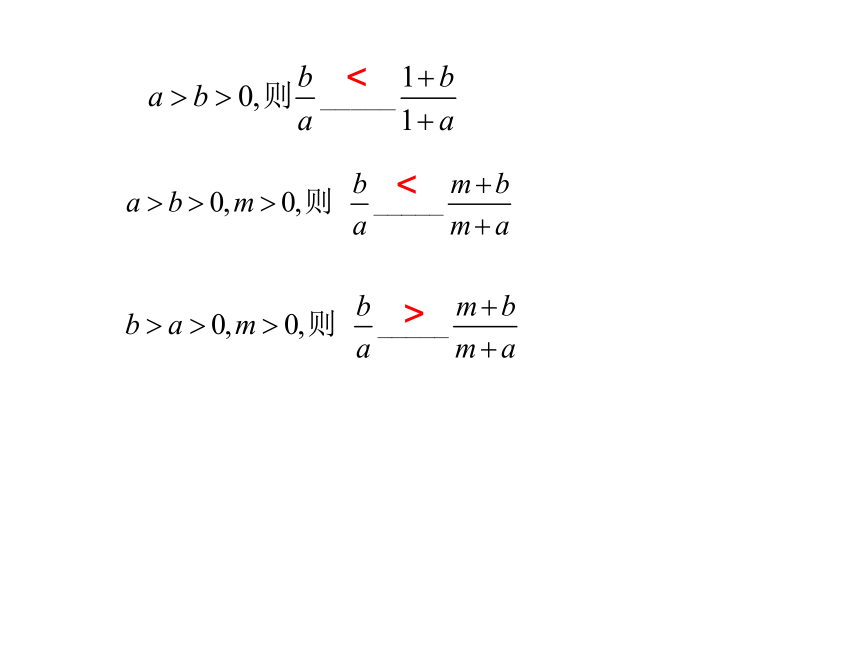
文档简介
课件14张PPT。§6.1:不等式的性质
(三)学习要求:
1. 复习不等式的十大性质和法则.
2..能熟练应用不等式的性质解题(3)可加性: a>b ? a+c>b+c.(5)开方法则: (1)对称性: a>b? bc ? a>c-b假真假假真注:(1)运用不等式的性质时,应注意不等式成立的条件。(2)一般地,要判断一个命题为真命题,必须严格加以证明,要判断一个命题为假命题,可举反例,或者由题中条件推出与结论相反的结果。一、典型例题讲评注意:同向不等式不能相减、相除!2.求取值范围的问题:例2.设f(x)=ax2+bx,且求 的取值范围。即:思考? 若二次函数y= f(x) 的图象过原点,且 已知函数f(x)=px2-q, -4≤f(1)≤-1,
-1≤f(2)≤5, 求f(3)的取值范围。-4≤f(1)≤-1-1≤f(2)≤5变式训练<><证明: a>b>0c<0每一步都要有依据(定理)证明: d>c>0a>b>0>02综合练习:DDCDBA解:比较大小的问题:分类讨论例5. 设 0<x<1,a>0 且 a≠1,试比较
| log a ( 1-x ) | 与 | log a ( 1 + x ) | 的大小。| log a ( 1-x ) | - | log a ( 1 + x ) | ∵ 0<x<1∴ 0<1-x<1,∴ | log a ( 1-x ) | > | log a ( 1 + x ) |解:(1) 当0绝对值1<1 + x <2| log a ( 1-x ) | - | log a ( 1 + x ) | ∴ | log a ( 1-x ) | > | log a ( 1 + x ) |(2) 当a>1时,则有:=-log a ( 1-x ) -log a ( 1 + x ) =-log a [( 1-x ) ( 1 + x )] | log a ( 1-x ) | > | log a ( 1 + x ) |.综上所述,对于0<x<1,a>0 且 a≠1的一切值总有还有另外方法吗?课堂小结:(1)用“特值法”解选择题、填空题1.比较大小的问题:(2)一般用“比差法”2.不等式的十大性质和法则:3.求取值范围的问题:注意:(1)减要改为加负,除应改为乘倒数注意:(2)取倒数时常要讨论作业:同步作业本P4
1. 复习不等式的十大性质和法则.
2..能熟练应用不等式的性质解题(3)可加性: a>b ? a+c>b+c.(5)开方法则: (1)对称性: a>b? b
-1≤f(2)≤5, 求f(3)的取值范围。-4≤f(1)≤-1-1≤f(2)≤5变式训练<><证明: a>b>0c<0每一步都要有依据(定理)证明: d>c>0a>b>0>02综合练习:DDCDBA解:比较大小的问题:分类讨论例5. 设 0<x<1,a>0 且 a≠1,试比较
| log a ( 1-x ) | 与 | log a ( 1 + x ) | 的大小。| log a ( 1-x ) | - | log a ( 1 + x ) | ∵ 0<x<1∴ 0<1-x<1,∴ | log a ( 1-x ) | > | log a ( 1 + x ) |解:(1) 当0
