第九章 概率初步 3 等可能事件的概率 第2课时 求简单的几何概率(含答案)
文档属性
| 名称 | 第九章 概率初步 3 等可能事件的概率 第2课时 求简单的几何概率(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章 概率初步
3 等可能事件的概率
第2课时 求简单的几何概率
基 础 练
知识点 求简单的几何概率
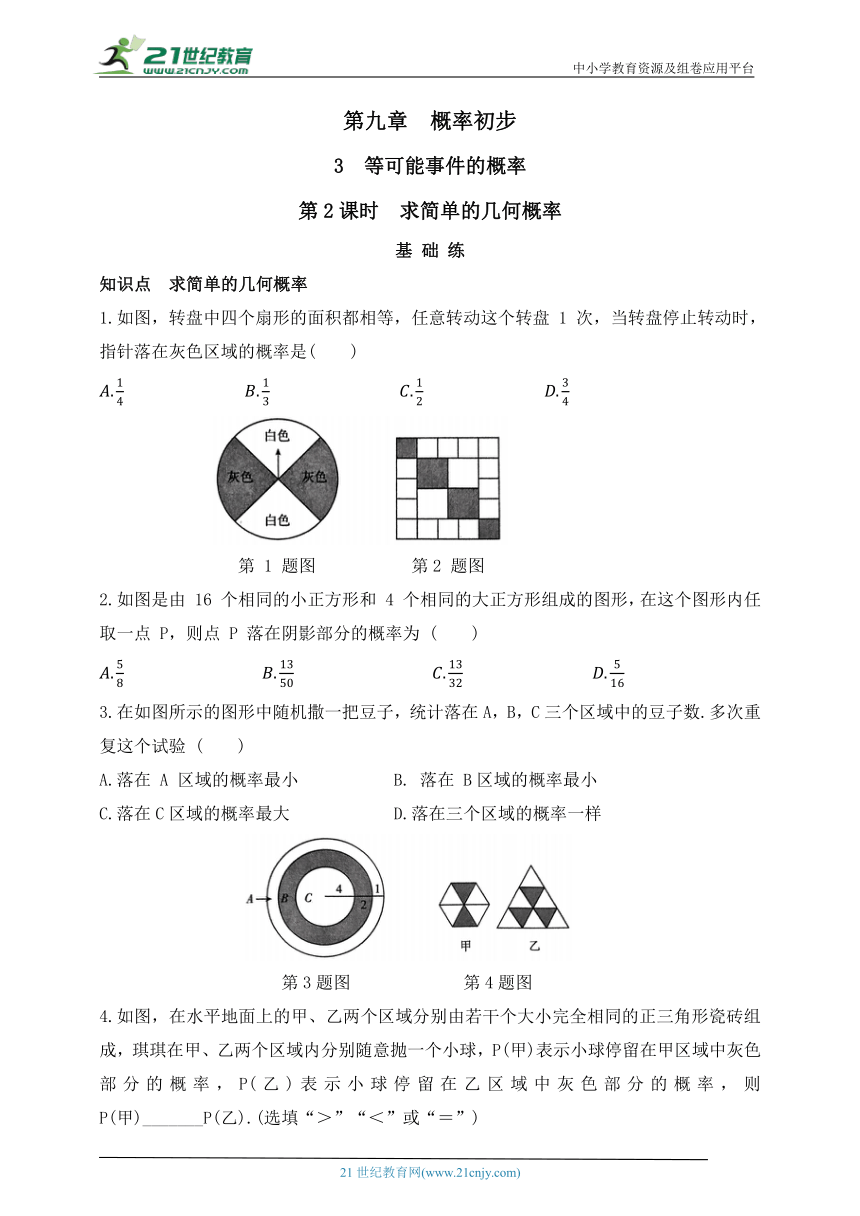
1.如图,转盘中四个扇形的面积都相等,任意转动这个转盘 1 次,当转盘停止转动时,指针落在灰色区域的概率是( )
第 1 题图 第2 题图
2.如图是由 16 个相同的小正方形和 4 个相同的大正方形组成的图形,在这个图形内任取一点 P,则点 P 落在阴影部分的概率为 ( )
3.在如图所示的图形中随机撒一把豆子,统计落在A,B,C三个区域中的豆子数.多次重复这个试验 ( )
A.落在 A 区域的概率最小 B. 落在 B区域的概率最小
C.落在C区域的概率最大 D.落在三个区域的概率一样
第3题图 第4题图
4.如图,在水平地面上的甲、乙两个区域分别由若干个大小完全相同的正三角形瓷砖组成,琪琪在甲、乙两个区域内分别随意抛一个小球,P(甲)表示小球停留在甲区域中灰色部分的概率,P(乙)表示小球停留在乙区域中灰色部分的概率,则 P(甲)_______P(乙).(选填“>”“<”或“=”)
5.“十一”黄金周期间,某购物广场举办迎国庆有奖销售活动,每购物满 100元,就会有一次转动大转盘的机会,请你根据大转盘(如图)来计算:
(1)享受七折优惠的概率;
(2)得 20 元的概率;
(3)得10元的概率;
(4)中奖得钱的概率是多少
提 升 练
6.如图,是一块三角形纸板,其中 一只蚂蚁在这张纸上自由爬行,则蚂蚁踩到阴影部分的概率为__________.
第6题图 第7题图
7.七巧板游戏是中国人的智慧结晶,如图,七巧板是由7 个几何图形组成的正方形,其中1,3,5,6,7 是等腰直角三角形,4是正方形,2是平行四边形.一只蚂蚁在七巧板上随机停留,刚巧停在2号板区域的概率是___________.
8.向如图所示的正三角形区域内扔沙包(区域中每个小正三角形除颜色外完全相同),沙包随机落在某个正三角形内.
(1)扔沙包一次,落在图中阴影区域的概率是___________;
(2)要使沙包落在图中阴影区域和空白区域的概率均为 还要涂黑几个小正三角形 请在图中画出.
9.小南发现操场中有一个不规则的封闭图形 ABC. 为了知道它的面积,他在封闭图形内画出了一个半径为 1 米的圆,在不远处向圈内掷石子,若石子落在图形ABC 以外,则重掷.记录如下:
石子落在圆内 (含圆上)的次数 14 43 93 150
石子落在阴影内 的次数 23 91 186 300
根据以上的数据,小南得到了封闭图形 ABC的面积.
请根据以上信息,回答以下问题:
(1)求石子落在阴影内的频率;
(2)估计封闭图形 ABC的面积.
10.综合与实践
(1)【问题再现】
课本中有这样一道概率题:如图1,这是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在蓝色区域和橙色区域的概率分别是多少 请你解答.
(2)【类比设计】
在元旦晚会上班长想设计一个摇奖转盘.请你在图 2 中设计一个转盘,自由转动这个转盘,当它停止转动时,三等奖:指针落在红色区域的概率为 二等奖:指针落在白色区
域的概率为 一等奖:指针落在黄色区域的概率为 .
(3)【拓展运用】
在一次促销活动中,某商场为了吸引顾客,设立转盘,转盘被平均分为 10 份,顾客每消费200 元转动 1次,对准红1份、黄2份、绿3份区域,分别得奖金100元、50元、30元购物券,求转动 1次所获购物券的平均数.
参考答案
1. C 2. B 3. A 4.=
5.解:(1)享受七折优惠的概率为
(2)得 20元的概率为
(3)得 10元的概率为
(4)中奖得钱的概率是
6. 7.
8.解:
(2)如图所示:
要使沙包落在图中阴影区域和空白区域的概率均为 还要涂黑2 个小正三角形(答案不唯一).
9.解:(1)观察表格得:随着投掷次数的增大,石子落在阴影内的频率为
(2)设封闭图形的面积为 a,小石子落在圆内(含圆上)的频率值稳定在
根据题意,得 解得 a=3π,
则封闭图形 ABC 的面积为 3π.
10.解:(1)根据几何概率的意义可知,
(2)根据题意,将转盘平均分成 6 份,
则:红色占: (份);白色占: (份);黄色占: (份).
如图所示:(答案不唯一)
(3)由题意,得
转动 1次的平均数为 (元).
答:转动1 次所获购物券的平均数是 29元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 概率初步
3 等可能事件的概率
第2课时 求简单的几何概率
基 础 练
知识点 求简单的几何概率
1.如图,转盘中四个扇形的面积都相等,任意转动这个转盘 1 次,当转盘停止转动时,指针落在灰色区域的概率是( )
第 1 题图 第2 题图
2.如图是由 16 个相同的小正方形和 4 个相同的大正方形组成的图形,在这个图形内任取一点 P,则点 P 落在阴影部分的概率为 ( )
3.在如图所示的图形中随机撒一把豆子,统计落在A,B,C三个区域中的豆子数.多次重复这个试验 ( )
A.落在 A 区域的概率最小 B. 落在 B区域的概率最小
C.落在C区域的概率最大 D.落在三个区域的概率一样
第3题图 第4题图
4.如图,在水平地面上的甲、乙两个区域分别由若干个大小完全相同的正三角形瓷砖组成,琪琪在甲、乙两个区域内分别随意抛一个小球,P(甲)表示小球停留在甲区域中灰色部分的概率,P(乙)表示小球停留在乙区域中灰色部分的概率,则 P(甲)_______P(乙).(选填“>”“<”或“=”)
5.“十一”黄金周期间,某购物广场举办迎国庆有奖销售活动,每购物满 100元,就会有一次转动大转盘的机会,请你根据大转盘(如图)来计算:
(1)享受七折优惠的概率;
(2)得 20 元的概率;
(3)得10元的概率;
(4)中奖得钱的概率是多少
提 升 练
6.如图,是一块三角形纸板,其中 一只蚂蚁在这张纸上自由爬行,则蚂蚁踩到阴影部分的概率为__________.
第6题图 第7题图
7.七巧板游戏是中国人的智慧结晶,如图,七巧板是由7 个几何图形组成的正方形,其中1,3,5,6,7 是等腰直角三角形,4是正方形,2是平行四边形.一只蚂蚁在七巧板上随机停留,刚巧停在2号板区域的概率是___________.
8.向如图所示的正三角形区域内扔沙包(区域中每个小正三角形除颜色外完全相同),沙包随机落在某个正三角形内.
(1)扔沙包一次,落在图中阴影区域的概率是___________;
(2)要使沙包落在图中阴影区域和空白区域的概率均为 还要涂黑几个小正三角形 请在图中画出.
9.小南发现操场中有一个不规则的封闭图形 ABC. 为了知道它的面积,他在封闭图形内画出了一个半径为 1 米的圆,在不远处向圈内掷石子,若石子落在图形ABC 以外,则重掷.记录如下:
石子落在圆内 (含圆上)的次数 14 43 93 150
石子落在阴影内 的次数 23 91 186 300
根据以上的数据,小南得到了封闭图形 ABC的面积.
请根据以上信息,回答以下问题:
(1)求石子落在阴影内的频率;
(2)估计封闭图形 ABC的面积.
10.综合与实践
(1)【问题再现】
课本中有这样一道概率题:如图1,这是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在蓝色区域和橙色区域的概率分别是多少 请你解答.
(2)【类比设计】
在元旦晚会上班长想设计一个摇奖转盘.请你在图 2 中设计一个转盘,自由转动这个转盘,当它停止转动时,三等奖:指针落在红色区域的概率为 二等奖:指针落在白色区
域的概率为 一等奖:指针落在黄色区域的概率为 .
(3)【拓展运用】
在一次促销活动中,某商场为了吸引顾客,设立转盘,转盘被平均分为 10 份,顾客每消费200 元转动 1次,对准红1份、黄2份、绿3份区域,分别得奖金100元、50元、30元购物券,求转动 1次所获购物券的平均数.
参考答案
1. C 2. B 3. A 4.=
5.解:(1)享受七折优惠的概率为
(2)得 20元的概率为
(3)得 10元的概率为
(4)中奖得钱的概率是
6. 7.
8.解:
(2)如图所示:
要使沙包落在图中阴影区域和空白区域的概率均为 还要涂黑2 个小正三角形(答案不唯一).
9.解:(1)观察表格得:随着投掷次数的增大,石子落在阴影内的频率为
(2)设封闭图形的面积为 a,小石子落在圆内(含圆上)的频率值稳定在
根据题意,得 解得 a=3π,
则封闭图形 ABC 的面积为 3π.
10.解:(1)根据几何概率的意义可知,
(2)根据题意,将转盘平均分成 6 份,
则:红色占: (份);白色占: (份);黄色占: (份).
如图所示:(答案不唯一)
(3)由题意,得
转动 1次的平均数为 (元).
答:转动1 次所获购物券的平均数是 29元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
