六年级下册数学北师大版2.4图形的放大和缩小(同步练习)(含答案)
文档属性
| 名称 | 六年级下册数学北师大版2.4图形的放大和缩小(同步练习)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 312.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-16 00:00:00 | ||
图片预览


文档简介
2.4图形的放大和缩小
一、选择题
1.把中的图形按照2∶1放大后的图形是( )。
A. B. C. D.
2.一张照片长3厘米,宽2厘米,现在按4:1放大,放大后这张照片的面积是原来面积的( )
A.4倍 B.8倍 C.16倍 D.5倍
3.在一张图纸上有400:1这样的一个比例.这个比例告诉我们的是( ).
A.图上距离是实际距离的
B.实际距离是图上距离的400倍
C.这张图纸是将实物放大到400倍画出来的
4.下列哪种情形图形的大小将发生变化( )。
A.平移 B.旋转 C.放缩
5.把一个正方形的边长按2∶1放大后,面积与原来的比是( )。
A.8∶1 B.6∶1 C.4∶1 D.2∶1
6.把长和宽分别为8厘米和6厘米的长方形的长和宽按1:2的比例缩小,所得到的长和宽分别为( )
A.16、12 B.12、16 C.4、3 D.3、4
7.如图所示的长方形按1:4缩小,所得的新长方形与原长方形的面积比是( ).
A.4:1 B.1:4 C.1:16 D.16:1
8.如下图,把图A按( )缩小得到图B.
A.1:2 B.2:1 C.1:4 D.4:1
二、填空题
9.把边长为5厘米的正方形按3∶1的比放大,放大后的正方形的边长是 厘米,周长是 厘米。
10.一个三角形底是20cm,高是15cm,把它按1∶5缩小后,底是( )cm,高是( )cm。
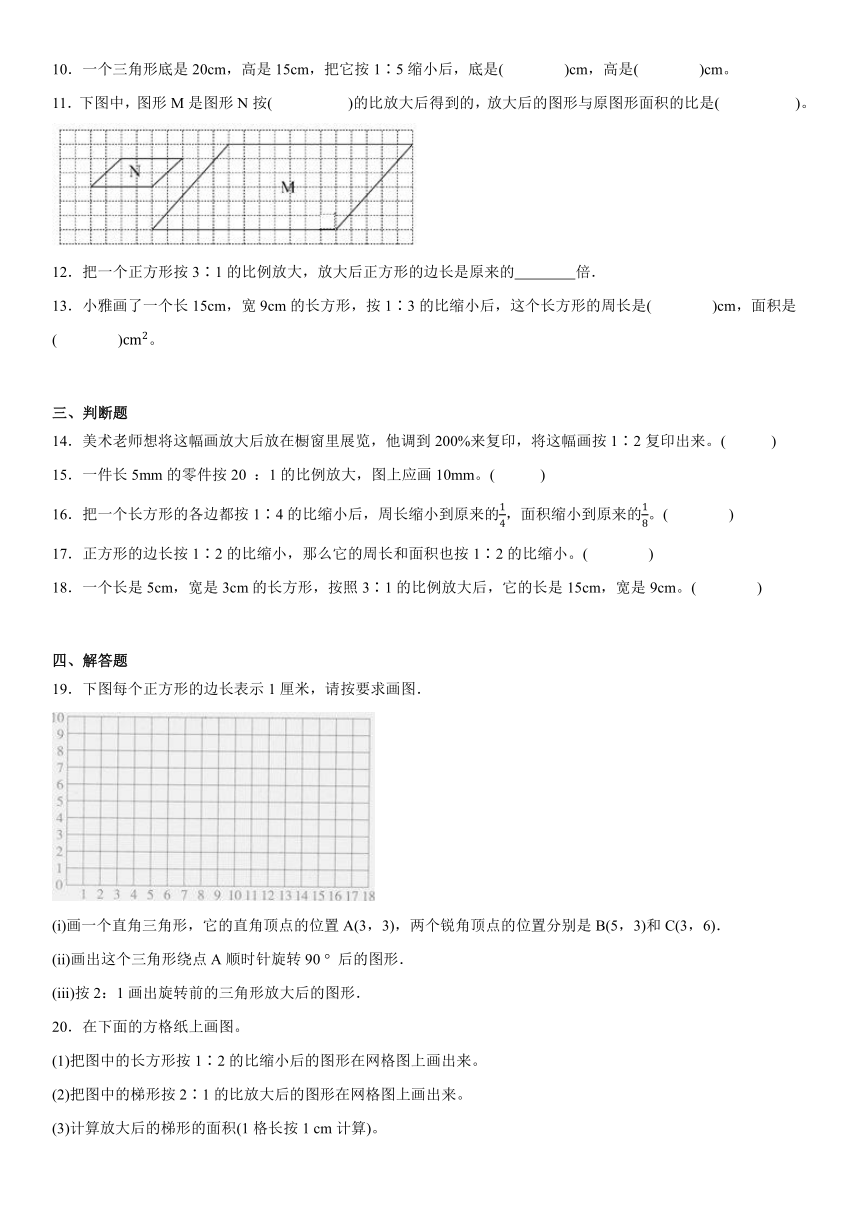
11.下图中,图形M是图形N按( )的比放大后得到的,放大后的图形与原图形面积的比是( )。
12.把一个正方形按3∶1的比例放大,放大后正方形的边长是原来的 倍.
13.小雅画了一个长15cm,宽9cm的长方形,按1∶3的比缩小后,这个长方形的周长是( )cm,面积是( )。
三、判断题
14.美术老师想将这幅画放大后放在橱窗里展览,他调到200%来复印,将这幅画按1∶2复印出来。( )
15.一件长5mm的零件按20 :1的比例放大,图上应画10mm。( )
16.把一个长方形的各边都按1∶4的比缩小后,周长缩小到原来的,面积缩小到原来的。( )
17.正方形的边长按1∶2的比缩小,那么它的周长和面积也按1∶2的比缩小。( )
18.一个长是5cm,宽是3cm的长方形,按照3∶1的比例放大后,它的长是15cm,宽是9cm。( )
四、解答题
19.下图每个正方形的边长表示1厘米,请按要求画图.
(i)画一个直角三角形,它的直角顶点的位置A(3,3),两个锐角顶点的位置分别是B(5,3)和C(3,6).
(ii)画出这个三角形绕点A顺时针旋转90 ° 后的图形.
(iii)按2:1画出旋转前的三角形放大后的图形.
20.在下面的方格纸上画图。
(1)把图中的长方形按1∶2的比缩小后的图形在网格图上画出来。
(2)把图中的梯形按2∶1的比放大后的图形在网格图上画出来。
(3)计算放大后的梯形的面积(1格长按1 cm计算)。
21.按要求填空并在方格纸上画出图形。(每个小正方形表示1平方厘米)
(1)①图①中,O点的位置用数对表示是( )。
②把图①绕O点逆时针旋转90°。
③把图①按2∶1的比放大。
(2)①图②中,以B点为观测点,C点在B点的( )偏( )( )°方向上。
②图②中,过A点作BC边上的高。
(3)图③中,已经涂了4个方格,请你再涂一个方格,使得5个方格组成的图形是轴对称图形,并画出它的对称轴。
22.下图中的每小格表示边长为1厘米的正方形。
(1)按3∶1画出三角形放大后的图形。
(2)放大后三角形的面积是( )平方厘米。
23.按要求在方格纸上画图并完成填空。
(1)把图形①绕点B逆时针旋转90°,画出旋转后的图形,旋转后点A的对应点的位置用数对表示是( )。
(2)图形①和旋转后的图形组合成了一个新的图形,画出这个组合图形的对称轴。
(3)图形②的圆心在点C的( )偏( )( )°方向上。
(4)把图形②按1∶2的比缩小,画出缩小后的图形。缩小后的图形面积是原来图形面积的。
24.红星小学为绿化社区设计了一个花坛,花坛的外围是一个边长6m的正方形,正方形里面是一个最大的圆,圆内是一个最大的正方形.
(1)用圆规和直尺把设计好的花坛按1:100画在下边方格图中.(方格图中每一小格的面积是1cm2)
(2)圆内正方形部分用来种植月季花,种植月季花的实际面积是( )m2.
参考答案:
1.B
2.C
3.C
4.C
5.C
6.C
7.C
8.A
9. 15 60
10. 4 3
11. 3∶1 9∶1
12.3
13. 16 15
14.×
15.×
16.×
17.×
18.√
19.解:(i)如图黑色部分;
(ii) 绕点A顺时针旋转90 ° 后的图形如图红色部分;
(iii) 放大后的图形的图形如图蓝色部分.
20.(1)(2)
(3)24cm2
21.(1)①②③
(2)①西偏南;45
②③见详解
22.36
23(1,2) 东;北;45 ;
24.(1)
(2)18
一、选择题
1.把中的图形按照2∶1放大后的图形是( )。
A. B. C. D.
2.一张照片长3厘米,宽2厘米,现在按4:1放大,放大后这张照片的面积是原来面积的( )
A.4倍 B.8倍 C.16倍 D.5倍
3.在一张图纸上有400:1这样的一个比例.这个比例告诉我们的是( ).
A.图上距离是实际距离的
B.实际距离是图上距离的400倍
C.这张图纸是将实物放大到400倍画出来的
4.下列哪种情形图形的大小将发生变化( )。
A.平移 B.旋转 C.放缩
5.把一个正方形的边长按2∶1放大后,面积与原来的比是( )。
A.8∶1 B.6∶1 C.4∶1 D.2∶1
6.把长和宽分别为8厘米和6厘米的长方形的长和宽按1:2的比例缩小,所得到的长和宽分别为( )
A.16、12 B.12、16 C.4、3 D.3、4
7.如图所示的长方形按1:4缩小,所得的新长方形与原长方形的面积比是( ).
A.4:1 B.1:4 C.1:16 D.16:1
8.如下图,把图A按( )缩小得到图B.
A.1:2 B.2:1 C.1:4 D.4:1
二、填空题
9.把边长为5厘米的正方形按3∶1的比放大,放大后的正方形的边长是 厘米,周长是 厘米。
10.一个三角形底是20cm,高是15cm,把它按1∶5缩小后,底是( )cm,高是( )cm。
11.下图中,图形M是图形N按( )的比放大后得到的,放大后的图形与原图形面积的比是( )。
12.把一个正方形按3∶1的比例放大,放大后正方形的边长是原来的 倍.
13.小雅画了一个长15cm,宽9cm的长方形,按1∶3的比缩小后,这个长方形的周长是( )cm,面积是( )。
三、判断题
14.美术老师想将这幅画放大后放在橱窗里展览,他调到200%来复印,将这幅画按1∶2复印出来。( )
15.一件长5mm的零件按20 :1的比例放大,图上应画10mm。( )
16.把一个长方形的各边都按1∶4的比缩小后,周长缩小到原来的,面积缩小到原来的。( )
17.正方形的边长按1∶2的比缩小,那么它的周长和面积也按1∶2的比缩小。( )
18.一个长是5cm,宽是3cm的长方形,按照3∶1的比例放大后,它的长是15cm,宽是9cm。( )
四、解答题
19.下图每个正方形的边长表示1厘米,请按要求画图.
(i)画一个直角三角形,它的直角顶点的位置A(3,3),两个锐角顶点的位置分别是B(5,3)和C(3,6).
(ii)画出这个三角形绕点A顺时针旋转90 ° 后的图形.
(iii)按2:1画出旋转前的三角形放大后的图形.
20.在下面的方格纸上画图。
(1)把图中的长方形按1∶2的比缩小后的图形在网格图上画出来。
(2)把图中的梯形按2∶1的比放大后的图形在网格图上画出来。
(3)计算放大后的梯形的面积(1格长按1 cm计算)。
21.按要求填空并在方格纸上画出图形。(每个小正方形表示1平方厘米)
(1)①图①中,O点的位置用数对表示是( )。
②把图①绕O点逆时针旋转90°。
③把图①按2∶1的比放大。
(2)①图②中,以B点为观测点,C点在B点的( )偏( )( )°方向上。
②图②中,过A点作BC边上的高。
(3)图③中,已经涂了4个方格,请你再涂一个方格,使得5个方格组成的图形是轴对称图形,并画出它的对称轴。
22.下图中的每小格表示边长为1厘米的正方形。
(1)按3∶1画出三角形放大后的图形。
(2)放大后三角形的面积是( )平方厘米。
23.按要求在方格纸上画图并完成填空。
(1)把图形①绕点B逆时针旋转90°,画出旋转后的图形,旋转后点A的对应点的位置用数对表示是( )。
(2)图形①和旋转后的图形组合成了一个新的图形,画出这个组合图形的对称轴。
(3)图形②的圆心在点C的( )偏( )( )°方向上。
(4)把图形②按1∶2的比缩小,画出缩小后的图形。缩小后的图形面积是原来图形面积的。
24.红星小学为绿化社区设计了一个花坛,花坛的外围是一个边长6m的正方形,正方形里面是一个最大的圆,圆内是一个最大的正方形.
(1)用圆规和直尺把设计好的花坛按1:100画在下边方格图中.(方格图中每一小格的面积是1cm2)
(2)圆内正方形部分用来种植月季花,种植月季花的实际面积是( )m2.
参考答案:
1.B
2.C
3.C
4.C
5.C
6.C
7.C
8.A
9. 15 60
10. 4 3
11. 3∶1 9∶1
12.3
13. 16 15
14.×
15.×
16.×
17.×
18.√
19.解:(i)如图黑色部分;
(ii) 绕点A顺时针旋转90 ° 后的图形如图红色部分;
(iii) 放大后的图形的图形如图蓝色部分.
20.(1)(2)
(3)24cm2
21.(1)①②③
(2)①西偏南;45
②③见详解
22.36
23(1,2) 东;北;45 ;
24.(1)
(2)18
