2023-2024深圳北师大版九下开学考模拟 (含解析)
文档属性
| 名称 | 2023-2024深圳北师大版九下开学考模拟 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 849.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-16 09:22:06 | ||
图片预览



文档简介
2023-2024深圳市九下开学考模拟
一、选择题(共10题;共30分)
1.截面为扇环的几何体与长方体组成的摆件如图所示,它的主视图是( )
A. B.
C. D.
2.在项目化学习中,“水是生命之源”项目组为了解本地区人均淡水消耗量,需要从四名同学(两名男生,两名女生)中随机抽取两人,组成调查小组进行社会调查,恰好抽到一名男生和一名女生的概率是( )
A. B. C. D.
3.关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )
A.k≤﹣ B.k≤﹣ 且k≠0
C.k≥﹣ D.k≥﹣ 且k≠0
4.如图,中,点D,E分别在边上.若,,则的长为( )
A. B. C. D.3
5.我省加快新旧动能转换,促进企业创新发展.某企业一月份的营业额是1000万元,月平均增长率相同,今年第一季度的总营业额是3640万元.若设月平均增长率是 ,那么可列出的方程是( )
A.
B.
C.
D.
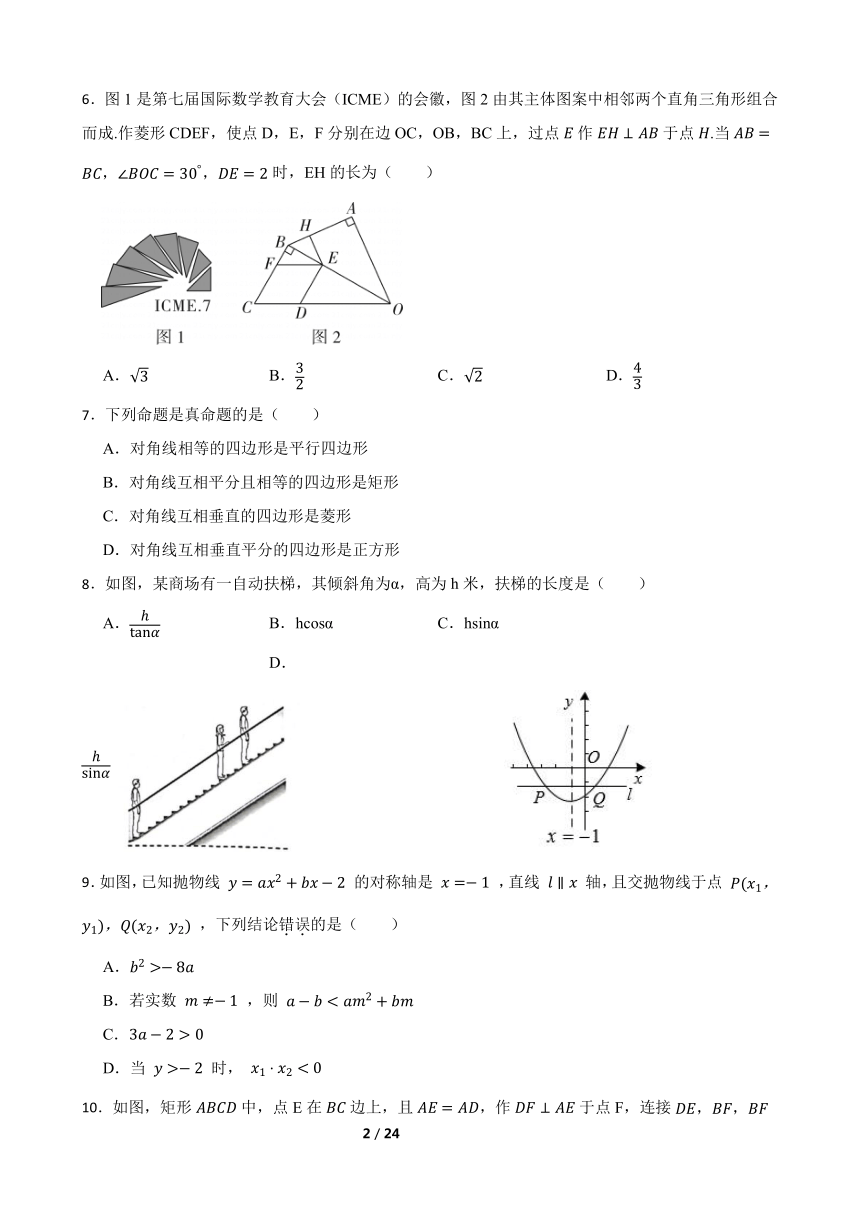
6.图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )
A. B. C. D.
7.下列命题是真命题的是( )
A.对角线相等的四边形是平行四边形
B.对角线互相平分且相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
8.如图,某商场有一自动扶梯,其倾斜角为α,高为h米,扶梯的长度是( )
A. B.hcosα C.hsinα D.
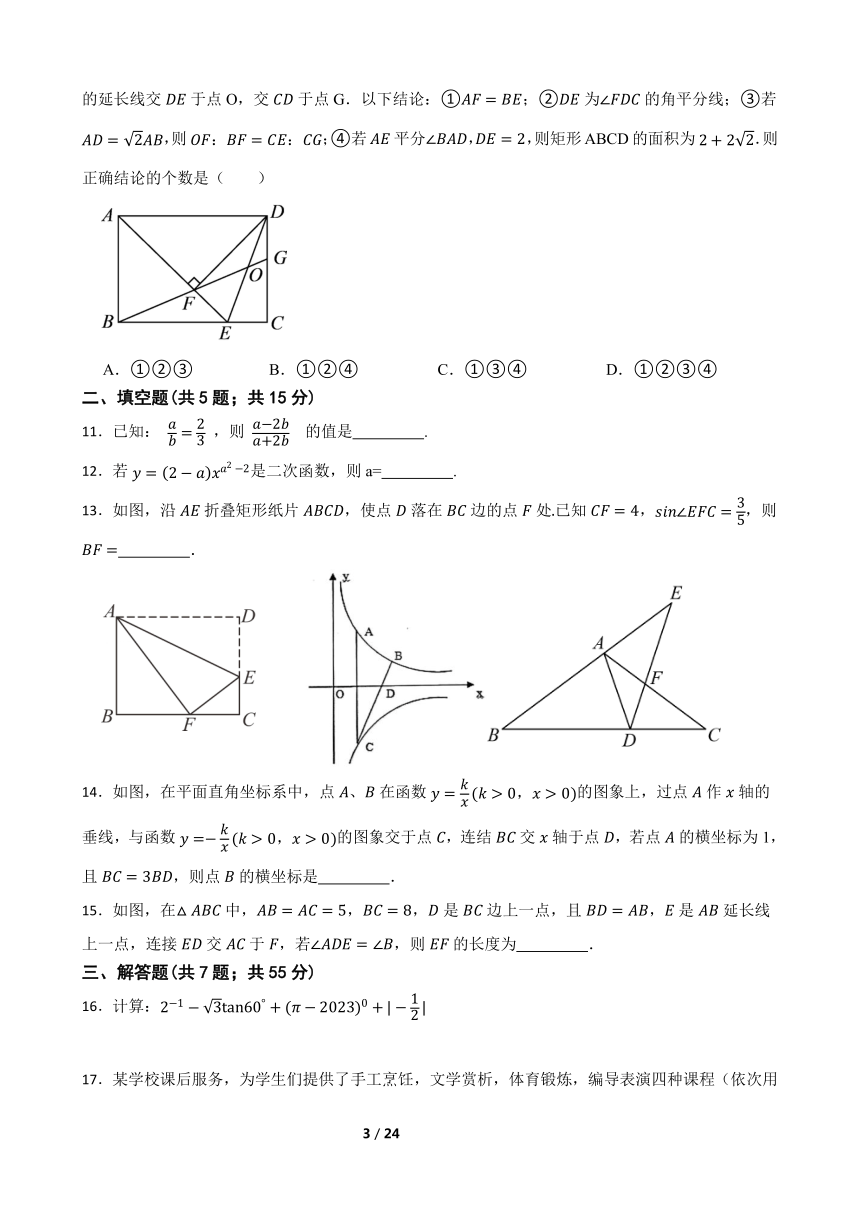
9.如图,已知抛物线 的对称轴是 ,直线 轴,且交抛物线于点 ,下列结论错误的是( )
A.
B.若实数 ,则
C.
D.当 时,
10.如图,矩形中,点E在边上,且,作于点F,连接的延长线交于点O,交于点G.以下结论:①;②为的角平分线;③若,则;④若平分,,则矩形ABCD的面积为.则正确结论的个数是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题(共5题;共15分)
11.已知: ,则 的值是 .
12.若是二次函数,则a= .
13.如图,沿折叠矩形纸片,使点落在边的点处已知,,则 .
14.如图,在平面直角坐标系中,点、在函数的图象上,过点作轴的垂线,与函数的图象交于点,连结交轴于点,若点的横坐标为1,且,则点的横坐标是 .
15.如图,在中,,,是边上一点,且,是延长线上一点,连接交于,若,则的长度为 .
三、解答题(共7题;共55分)
16.计算:
17.某学校课后服务,为学生们提供了手工烹饪,文学赏析,体育锻炼,编导表演四种课程(依次用A,B,C,D表示),为了解学生对这四种课程的将好情况:学校随机抽取部分学生进行了“你最喜欢哪一种课外活动(必选且只选一种)”的问卷调查,并根据调查结果绘制了条形统计图和扇形统计图,部分信息如图:
(1)参加问卷调查的学生人数是 人,扇形统计图中“D”对应扇形的圆心角的大小为 .
(2)估计全体1000名学生中最喜欢C活动的人数约为多少人?
(3)现从喜好编导表演的甲、乙、丙、丁四名学生中任选两人搭档彩排双人相声,请用树状图或列表法求恰好甲和丁同学被选到的概率是多少?
18.金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73)
19.参照学习函数的过程与方法,探究函数y= 的图象与性质.
因为y= ,即y=﹣ +1,所以我们对比函数y=﹣ 来探究.
列表:
x … ﹣4 ﹣3 ﹣2 ﹣1 ﹣ 1 2 3 4 …
y=﹣ … 1 2 4 ﹣4 ﹣2 ﹣1 ﹣ ﹣ …
y= … 2 3 5 ﹣3 ﹣1 0 …
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y= 相应的函数值为纵坐标,描出相应的点,如图所示:
(1) 请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2) 观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y= 的图象是由y=﹣ 的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3) 设A(x1,y1),B(x2,y2)是函数y= 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
20.如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
(1)求证:△ABD∽△DCE;
(2)当△ADE是等腰三角形时,求AE的长.
21. 【阅读理解】已知关于、的二次函数,它的顶点坐标为,故不论取何值时,对应的二次函数的顶点都在直线上,我们称顶点位于同一条直线上且形状相同的抛物线为同源二次函数,该条直线为根函数.
(1)【问题解决】若二次函数和是同源二次函数,求它们的根函数;
(2)已知关于、的二次函数:,完成下列问题:
求满足二次函数的所有二次函数的根函数;
若二次函数与直线交于点,求点到轴的最小距离,请求出此时为何值?并求出点到轴的最小距离.
22.
(1)【问题初探】
如图1,等腰中,,点为边一点,以为腰向下作等腰,.连接,,点为的中点,连接.猜想并证明线段与的数量关系和位置关系.
(2)【深入探究】
在(1)的条件下,如图2,将等腰绕点旋转,上述结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)【拓展迁移】
如图3,等腰中,,.在中,, .连接,,点为的中点,连接.
绕点旋转过程中,
①线段与的数量关系为: ;
②若,,当点在等腰内部且的度数最大时,线段的长度为 .
答案解析部分
1.【答案】A
【解析】【解答】解: 截面为扇环的几何体与长方体组成的摆件的主视图是A选项的图形.
故答案为:A.
【分析】主视图,就是从正面看得到的图形,看得见的轮廓线画成实线,看不见但又存在的轮廓线画成虚线,从而即可判断得出答案.
2.【答案】D
【解析】【解答】解:画树状图如下:
∴共有12种等可能的结果,其中一名男生和一名女生的结果数为8,
∴恰好抽到一名男生和一名女生的概率为:,
故答案为:D.
【分析】先画树状图,再求出共有12种等可能的结果,其中一名男生和一名女生的结果数为8,最后求概率即可。
3.【答案】D
【解析】【解答】解:∵关于x的一元二次方程kx2+3x﹣1=0有实数根,
∴△=b2﹣4ac≥0,
即:9+4k≥0,
解得:k≥﹣ ,
∵关于x的一元二次方程kx2+3x﹣1=0中k≠0,
则k的取值范围是k≥﹣ 且k≠0.
故选D.
【分析】根据方程根的情况可以判定其根的判别式的取值范围,进而可以得到关于k的不等式,解得即可,同时还应注意二次项系数不能为0.
4.【答案】C
【解析】【解答】解:∵
又∵∠DAE=∠CAB
∴△DAE∽△CAB
∴
∴DE=BC==
故答案为:C.
【分析】由两边对应成比例且夹角相等的两个三角形相似,可得△DAE∽△CAB,相似三角形的对应边之比等于相似比得,从而代入可算出DE的长.
5.【答案】C
【解析】【解答】解:设月平均增长的百分率是 ,则该超市二月份的营业额为 万元,三月份的营业额为 万元,
依题意,得 .
故答案为:C.
【分析】设月平均增长的百分率是 ,依据题意列方程即可.
6.【答案】C
【解析】【解答】解:∵四边形CDEF是菱形,DE=2,
∴CD=DE=CF=EF=2,CF∥DE,CD∥EF,
∴∠CBO=∠DEO=90°,∠BEF=∠BOC=30°
∴OD=2DE=4,OE=,BF=,BE=,
∴BC=CF+BF=3,BO=OE+BE=,
∵AB=BC,
∴AB=3,
在Rt△ABO中,由勾股定理得AO=,
∵HE⊥AB,
∴∠BHE=∠A=90°,
又∠HBE=∠ABO,
∴△BHE∽△BAO,
∴,即,
解得HE= .
故答案为: C.
【分析】由菱形的性质得CD=DE=CF=EF=2,CF∥DE,CD∥EF,由二直线平行,同位角相等,得∠CBO=∠DEO=90°,∠BEF=∠BOC=30°,然后根据直角三角形中,含30°角所对的直角边等于斜边的一半得OD=2DE=4,OE=,BF=,BE=,进而由线段的和差算出BC、OB的长,在Rt△ABO中,由勾股定理算出OA的长,然后判断出△BHE∽△BAO,最后相似三角形对应边成比例建立方程可求出HE的长.
7.【答案】B
【解析】【解答】解:A、对角线互相平分的四边形是平行四边形;故本选项错误,不符合题意;
B、对角线互相平分且相等的四边形是矩形;故本选项正确,符合题意;
C、对角线互相垂直的平行四边形是菱形;故本选项错误,不符合题意;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误,不符合题意;
故答案为:B.
【分析】利用正确的命题是真命题;利用平行四边形的判定定理,可对A作出判断;利用矩形的判定定理可对B作出判断;利用菱形的判定定理可对C作出判断;利用正方形的判定定理,可对D作出判断.
8.【答案】D
【解析】【解答】解:设扶梯的长度为x米,
根据题意,sinα=
解得x=
故答案为:D
【分析】设扶梯的长度为x米,利用正弦的定义得到sinα=,然后求出x即可.
9.【答案】C
【解析】【解答】解:∵抛物线 的对称轴是 ,
∴ ,
∴ ,
∵抛物线开口向上,
∴ ,
∴ ,
∴ ,故A说法正确,不符合题意;
∵抛物线开口向上,抛物线对称轴为直线x=-1,
∴当x=-1时, ,
∴当实数 ,则 ,
∴当实数 时, ,故B说法正确,不符合题意;
∵当 时, ,
∴a+2a-2<0,即3a-2<0,故C说法错误,符合题意;
∵ ,
∴直线l与抛物线的两个交点分别在y轴的两侧,
∴ ,故D说法正确,不符合题意.
故答案为:C.
【分析】根据对称轴为直线x=-1可得b=2a,根据图象开口向上得a>0,则b2+8a=4a2+8a>0,据此判断A;由图象得当x=-1时,函数取得最小值,ymin=a-b-2,进而判断B;当x=1时,y=a+b-2<0,结合b=2a可判断C;由图象可得直线l与抛物线的两个交点分别在y轴的两侧,据此判断D.
10.【答案】D
【解析】【解答】解:∵四边形是矩形,,
∴,
∴,
∵,
∴,
∴,故①正确;
②∵,
∴,,
∴,
∵,
∴,
∴,
∴为的角平分线,故②正确;
③连接,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,,
∴,
∵,
∴,
∴,
∴,,
∴, ,
∴,
∴,
∵,
∴,
∴,
∴,故③正确;
∵平分,
∴,
∴,
设,
∴,
∵,
∴,
解得:,
∴矩形的面积为:,故④正确;
故答案为:D.
【分析】分类讨论,利用矩形的性质,全等三角形的判定与性质,勾股定理计算求解即可。
11.【答案】
【解析】【解答】解:由 ,可设a=2k,b=3k,(k≠0),
故: ,
故答案: .
【分析】根据比例的性质,由 ,可设a=2k,b=3k,(k≠0),然后将a,b的值代入代数式,按整式的混合运算法则即可算出答案。
12.【答案】-2
【解析】【解答】解:∵函数y=是二次函数,
∴2﹣a≠0, ,
∴a≠2,
∴
故答案为:.
【分析】形如“y=ax2+bx+c(a、b、c都是常数,且a≠0)”的函数就是二次函数,据此可得2-a≠0且a2-2=2,求解即可.
13.【答案】6
【解析】【解答】解:在矩形纸片ABCD中,∠B =∠D= 90°,AD=BC,
由折叠性质得AF=AD=BC,∠AFE=∠D=∠B = 90°,
∴∠BAF+∠AFB = 90°,∠EFC+∠AFB=90°,
∴∠BAF=∠EFC,
在Rt△ABF中,
,
∵CF=4,
则,
解得BF= 6;
故答案为:6.
【分析】根据折叠性质和矩形性质得到AF=AD=BC,∠AFE=∠D=∠B=90°,根据等角的余角相等得到∠BAF=∠EFC,再根据,求解即可.
14.【答案】2
【解析】【解答】设点A的坐标为,设AC与x轴的交点为E,过点B作BF⊥x轴,垂足为F,如图,
∵点C在函数的图象上,且AC⊥x轴,
∴C的坐标为,
∴EC=k,
∵BF⊥x轴,CE⊥x轴,
∴ ,
∴ ,
又∵,
∴ ,
∴,
即,
∴点B的纵坐标为,代入反比例函数解析式:,
当时,,
∴B点的横坐标是2,
故答案为:2.
【分析】设点A的坐标为,设AC与x轴的交点为E,过点B作BF⊥x轴,垂足为F,先证明可得,再结合可得,求出,再将点B的坐标代入可得,求出k的值,即可得到点B的横坐标。
15.【答案】
【解析】【解答】解:过点A作AM⊥BC于点M,
∵AB=AC=5,BC=8,
∴BM=CM=4,
∴AM==3.
∵BD=AB=5,
∴DM=BD-BM=AB-BM=5-4=1,
∴AD=,CD=CM-DM=4-1=3.
∵AB=AC,
∴∠B=∠C.
∵∠ADE=∠B,
∴∠ADE=∠C.
∵BD=AB,
∴∠BAD=∠BDA.
∵∠BAD=∠ADE+∠E,∠BDA=∠C+∠DAC,
∴∠E=∠DAC,
∴△ADE∽△DCA,
∴,
∴DE=.
∵∠ADE=∠C,∠DAF=∠CAD,
∴△ADF∽△ACD,
∴,
∴DF=,
∴EF=DE-DF=-=.
故答案为:.
【分析】过点A作AM⊥BC于点M,由等腰三角形的性质可得BM=CM=4,利用勾股定理可得AM,然后求出DM、AD,根据等腰三角形的性质可得∠B=∠C,结合∠ADE=∠B可得∠ADE=∠C,利用两角对应相等的两个三角形相似可得△ADE∽△DCA、△ADF∽△ACD,由相似三角形的性质可得DE、DF,然后根据EF=DE-DF进行计算.
16.【答案】解:原式
【解析】【分析】先代入特殊锐角三角函数值,同时根据负整数指数幂的性质、0指数幂的性质及绝对值的性质分别化简,然后再计算二次根式的乘法,最后计算有理数的加减法即可得出答案.
17.【答案】(1)240;36°
(2)解:最喜欢D活动的人数占总调查人数:,
∴最喜欢C活动的人数占总调查人数:1-35%-25%-10%=30%,
∴1000名学生中最喜欢C活动的人数约有:人.
(3)树状图如下:
恰好选到甲和丁同学有2种情况,总的情况有12种,
∴恰好选到甲和丁同学的概率为.
18.【答案】解:过点C作CM⊥AB于M.则四边形MEDC是矩形,
∴ME=DC=3.CM=ED,
在Rt△AEF中,∠AFE=60°,设EF=x,则AF=2x,AE= x,
在Rt△FCD中,CD=3,∠CFD=30°,
∴DF=3 ,
在Rt△AMC中,∠ACM=45°,
∴∠MAC=∠ACM=45°,
∴MA=MC,
∵ED=CM,
∴AM=ED,
∵AM=AE﹣ME,ED=EF+DF,
∴ x﹣3=x+3 ,
∴x=6+3 ,
∴AE= (6+3 )=6 +9,
∴AB=AE﹣BE=9+6 ﹣1≈18.4米.
答:旗杆AB的高度约为18.4米.
【解析】【分析】过点C作CM⊥AB于M.则四边形MEDC是矩形,设EF=x,根据AM=DE,列出方程即可解决问题.
19.【答案】(1) 解:函数图象如图所示:
(2)增大;上;1;(0,1)
(3) 解:∵x1+x2=0,
∴x1=﹣x2,
∴A(x1,y1),B(x2,y2)关于(0,1)对称,
∴y1+y2=2,
∴y1+y2+3=5
【解析】【解答】解:(2)①当x<0时,y随x的增大而增大;
②y= 的图象是由y=﹣ 的图象向上平移1个单位而得到;
③图象关于点(0,1)中心对称.(填点的坐标)
故答案为增大,上,1,(0,1)
【分析】(1)利用描点法,画出函数的图象。
(2)①观察函数图象,进行分析可知x<0时,y随x的变化情况;②观察函数的图象,可知可得到两图像的平移规律;③然后就可得到y= 的图像是关于(0,1)对称。
(3)由x1+x2=0,可得到x1=﹣x2,再由A(x1,y1),B(x2,y2)关于(0,1)对称,就可求出y1+y2,然后整体代入可求解。
20.【答案】(1)证明:Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=45°,
∴45°+∠EDC=45°+∠BAD.
∴∠EDC=∠BAD.
∴△ABD∽△DCE.
(2)解:讨论:①若AD=AE时,∠DAE=90°,此时D点与点B重合,不合题意.
②若AD=DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,
于是AB=AC=2,BC=2,AE=AC﹣EC=2﹣BD=2﹣(2﹣2)=4﹣2
③若AE=DE,此时∠DAE=∠ADE=45°,
如下图所示易知AD⊥BC,DE⊥AC,且AD=DC.由等腰三角形的三线合一可知:AE=CE=AC=1.
【解析】【分析】(1)首先根据等腰直角三角形的两个底角都是45°,得到一对对应角相等;再根据三角形的外角的性质得到∠ADE+∠EDC=∠B+∠BAD,从而证明∠EDC=∠BAD,根据两个角对应相等,得到两个三角形相似;
(2)根据等腰三角形的定义,此题要分三种情况进行分析讨论.根据等腰三角形的性质进行计算.
21.【答案】(1)解:,
该抛物线的顶点为;
,
该抛物线的顶点坐标为.
设经过点和点的直线的解析式为,
,
解得:.
.
它们的根函数为直线.
(2)解:,
该抛物线的顶点坐标为,
设顶点在直线上,
.
解得:,
顶点在直线上,
满足二次函数的所有二次函数的根函数为.
二次函数与直线交于点,
.
.
,
点的纵坐标当时,由最小值为.
点到轴的最小距离为,此时.
【解析】【分析】(1)首先根据配方法分别求出两条抛物线的顶点坐标,然后根据根函数的定义,设出直线解析式,将两个顶点坐标代入所设的直线解析式中求出即可.
(2)①首先根据配方法求出二次函数的顶点坐标,然后根据根函数的定义,代入定点左边即可求出根函数的解析式.
②先根据二次函数与直线x=-3交于点P,求出点P的坐标,然后算出点P到x轴的距离,对其配方即可求出最小值.
22.【答案】(1)解:,,理由如下:
如图,延长交于点,
为等腰直角三角形,,
,
为等腰直角三角形,,
,,
又,
,
,
在中,点为斜边的中点,
,
,
设,则,
,
,
在,点为斜边的中点,
,
,
,
,
;
(2)解:结论,,仍然成立,理由如下:
如图,取的中点,连接,,延长分别交,于点,,
点,分别是,的中点,
,
,
,
在等腰中,点是的中点,
,,
,
点,分别是,的中点,
,
,
,
,
,
,
,即,
,
,
在和中,
,,
,即.
综上:,;
(3);
【解析】【解答】解:(3)①如图,取的中点,连接,,延长分别交,于点,
∵,,
∴,
∵,
∴,
∴,
∴,
点,分别是,的中点,
,,
,
在等腰中,点是的中点,,
,,,
∴,
∴,即,
,
点,分别是,的中点,
,
,
,
,
,
,
,
∴;
故答案为:
②∵,,
∴点D在以点B为圆心,长为半径的圆上运动,
∴当时,最大,
过点E作,
∴,
∴四边形为矩形,
∴,
在中,,
在中,,,
∴,
∴,
在中, ,
由①得:,
.
【分析】(1),,理由:延长交于点,根据SAS证明△DBC≌△EBC,可得CD=CE,根据直角三角形斜边中线的性质可得AF=CD=CE, 设,则, 由全等三角形的性质可得,再根据直角三角形斜边中线的性质可得AF=CF,利用等腰三角形的性质及三角形内角和求出∠FPC=90°,继而得解;
(2)仍然成立,理由:取的中点,连接,,延长分别交,于点,, 根据三角形中位线定理及等腰直角三角形可得 , 再证明, 可得 ,,继而得解;
(3)①取的中点,连接,,延长分别交,于点,,根据等腰三角形及直角三角形的性质可得,再证,利用相似三角形的性质即可求解;②判断出点D在以点B为圆心,长为半径的圆上运动,则当时,最大,过点E作,则四边形为矩形,可得,由勾股定理求出CD,从而得出CH,在中,由勾股定理求出CE,继而得解.
1 / 1
一、选择题(共10题;共30分)
1.截面为扇环的几何体与长方体组成的摆件如图所示,它的主视图是( )
A. B.
C. D.
2.在项目化学习中,“水是生命之源”项目组为了解本地区人均淡水消耗量,需要从四名同学(两名男生,两名女生)中随机抽取两人,组成调查小组进行社会调查,恰好抽到一名男生和一名女生的概率是( )
A. B. C. D.
3.关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )
A.k≤﹣ B.k≤﹣ 且k≠0
C.k≥﹣ D.k≥﹣ 且k≠0
4.如图,中,点D,E分别在边上.若,,则的长为( )
A. B. C. D.3
5.我省加快新旧动能转换,促进企业创新发展.某企业一月份的营业额是1000万元,月平均增长率相同,今年第一季度的总营业额是3640万元.若设月平均增长率是 ,那么可列出的方程是( )
A.
B.
C.
D.
6.图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )
A. B. C. D.
7.下列命题是真命题的是( )
A.对角线相等的四边形是平行四边形
B.对角线互相平分且相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
8.如图,某商场有一自动扶梯,其倾斜角为α,高为h米,扶梯的长度是( )
A. B.hcosα C.hsinα D.
9.如图,已知抛物线 的对称轴是 ,直线 轴,且交抛物线于点 ,下列结论错误的是( )
A.
B.若实数 ,则
C.
D.当 时,
10.如图,矩形中,点E在边上,且,作于点F,连接的延长线交于点O,交于点G.以下结论:①;②为的角平分线;③若,则;④若平分,,则矩形ABCD的面积为.则正确结论的个数是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题(共5题;共15分)
11.已知: ,则 的值是 .
12.若是二次函数,则a= .
13.如图,沿折叠矩形纸片,使点落在边的点处已知,,则 .
14.如图,在平面直角坐标系中,点、在函数的图象上,过点作轴的垂线,与函数的图象交于点,连结交轴于点,若点的横坐标为1,且,则点的横坐标是 .
15.如图,在中,,,是边上一点,且,是延长线上一点,连接交于,若,则的长度为 .
三、解答题(共7题;共55分)
16.计算:
17.某学校课后服务,为学生们提供了手工烹饪,文学赏析,体育锻炼,编导表演四种课程(依次用A,B,C,D表示),为了解学生对这四种课程的将好情况:学校随机抽取部分学生进行了“你最喜欢哪一种课外活动(必选且只选一种)”的问卷调查,并根据调查结果绘制了条形统计图和扇形统计图,部分信息如图:
(1)参加问卷调查的学生人数是 人,扇形统计图中“D”对应扇形的圆心角的大小为 .
(2)估计全体1000名学生中最喜欢C活动的人数约为多少人?
(3)现从喜好编导表演的甲、乙、丙、丁四名学生中任选两人搭档彩排双人相声,请用树状图或列表法求恰好甲和丁同学被选到的概率是多少?
18.金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73)
19.参照学习函数的过程与方法,探究函数y= 的图象与性质.
因为y= ,即y=﹣ +1,所以我们对比函数y=﹣ 来探究.
列表:
x … ﹣4 ﹣3 ﹣2 ﹣1 ﹣ 1 2 3 4 …
y=﹣ … 1 2 4 ﹣4 ﹣2 ﹣1 ﹣ ﹣ …
y= … 2 3 5 ﹣3 ﹣1 0 …
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y= 相应的函数值为纵坐标,描出相应的点,如图所示:
(1) 请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2) 观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y= 的图象是由y=﹣ 的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3) 设A(x1,y1),B(x2,y2)是函数y= 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
20.如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
(1)求证:△ABD∽△DCE;
(2)当△ADE是等腰三角形时,求AE的长.
21. 【阅读理解】已知关于、的二次函数,它的顶点坐标为,故不论取何值时,对应的二次函数的顶点都在直线上,我们称顶点位于同一条直线上且形状相同的抛物线为同源二次函数,该条直线为根函数.
(1)【问题解决】若二次函数和是同源二次函数,求它们的根函数;
(2)已知关于、的二次函数:,完成下列问题:
求满足二次函数的所有二次函数的根函数;
若二次函数与直线交于点,求点到轴的最小距离,请求出此时为何值?并求出点到轴的最小距离.
22.
(1)【问题初探】
如图1,等腰中,,点为边一点,以为腰向下作等腰,.连接,,点为的中点,连接.猜想并证明线段与的数量关系和位置关系.
(2)【深入探究】
在(1)的条件下,如图2,将等腰绕点旋转,上述结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)【拓展迁移】
如图3,等腰中,,.在中,, .连接,,点为的中点,连接.
绕点旋转过程中,
①线段与的数量关系为: ;
②若,,当点在等腰内部且的度数最大时,线段的长度为 .
答案解析部分
1.【答案】A
【解析】【解答】解: 截面为扇环的几何体与长方体组成的摆件的主视图是A选项的图形.
故答案为:A.
【分析】主视图,就是从正面看得到的图形,看得见的轮廓线画成实线,看不见但又存在的轮廓线画成虚线,从而即可判断得出答案.
2.【答案】D
【解析】【解答】解:画树状图如下:
∴共有12种等可能的结果,其中一名男生和一名女生的结果数为8,
∴恰好抽到一名男生和一名女生的概率为:,
故答案为:D.
【分析】先画树状图,再求出共有12种等可能的结果,其中一名男生和一名女生的结果数为8,最后求概率即可。
3.【答案】D
【解析】【解答】解:∵关于x的一元二次方程kx2+3x﹣1=0有实数根,
∴△=b2﹣4ac≥0,
即:9+4k≥0,
解得:k≥﹣ ,
∵关于x的一元二次方程kx2+3x﹣1=0中k≠0,
则k的取值范围是k≥﹣ 且k≠0.
故选D.
【分析】根据方程根的情况可以判定其根的判别式的取值范围,进而可以得到关于k的不等式,解得即可,同时还应注意二次项系数不能为0.
4.【答案】C
【解析】【解答】解:∵
又∵∠DAE=∠CAB
∴△DAE∽△CAB
∴
∴DE=BC==
故答案为:C.
【分析】由两边对应成比例且夹角相等的两个三角形相似,可得△DAE∽△CAB,相似三角形的对应边之比等于相似比得,从而代入可算出DE的长.
5.【答案】C
【解析】【解答】解:设月平均增长的百分率是 ,则该超市二月份的营业额为 万元,三月份的营业额为 万元,
依题意,得 .
故答案为:C.
【分析】设月平均增长的百分率是 ,依据题意列方程即可.
6.【答案】C
【解析】【解答】解:∵四边形CDEF是菱形,DE=2,
∴CD=DE=CF=EF=2,CF∥DE,CD∥EF,
∴∠CBO=∠DEO=90°,∠BEF=∠BOC=30°
∴OD=2DE=4,OE=,BF=,BE=,
∴BC=CF+BF=3,BO=OE+BE=,
∵AB=BC,
∴AB=3,
在Rt△ABO中,由勾股定理得AO=,
∵HE⊥AB,
∴∠BHE=∠A=90°,
又∠HBE=∠ABO,
∴△BHE∽△BAO,
∴,即,
解得HE= .
故答案为: C.
【分析】由菱形的性质得CD=DE=CF=EF=2,CF∥DE,CD∥EF,由二直线平行,同位角相等,得∠CBO=∠DEO=90°,∠BEF=∠BOC=30°,然后根据直角三角形中,含30°角所对的直角边等于斜边的一半得OD=2DE=4,OE=,BF=,BE=,进而由线段的和差算出BC、OB的长,在Rt△ABO中,由勾股定理算出OA的长,然后判断出△BHE∽△BAO,最后相似三角形对应边成比例建立方程可求出HE的长.
7.【答案】B
【解析】【解答】解:A、对角线互相平分的四边形是平行四边形;故本选项错误,不符合题意;
B、对角线互相平分且相等的四边形是矩形;故本选项正确,符合题意;
C、对角线互相垂直的平行四边形是菱形;故本选项错误,不符合题意;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误,不符合题意;
故答案为:B.
【分析】利用正确的命题是真命题;利用平行四边形的判定定理,可对A作出判断;利用矩形的判定定理可对B作出判断;利用菱形的判定定理可对C作出判断;利用正方形的判定定理,可对D作出判断.
8.【答案】D
【解析】【解答】解:设扶梯的长度为x米,
根据题意,sinα=
解得x=
故答案为:D
【分析】设扶梯的长度为x米,利用正弦的定义得到sinα=,然后求出x即可.
9.【答案】C
【解析】【解答】解:∵抛物线 的对称轴是 ,
∴ ,
∴ ,
∵抛物线开口向上,
∴ ,
∴ ,
∴ ,故A说法正确,不符合题意;
∵抛物线开口向上,抛物线对称轴为直线x=-1,
∴当x=-1时, ,
∴当实数 ,则 ,
∴当实数 时, ,故B说法正确,不符合题意;
∵当 时, ,
∴a+2a-2<0,即3a-2<0,故C说法错误,符合题意;
∵ ,
∴直线l与抛物线的两个交点分别在y轴的两侧,
∴ ,故D说法正确,不符合题意.
故答案为:C.
【分析】根据对称轴为直线x=-1可得b=2a,根据图象开口向上得a>0,则b2+8a=4a2+8a>0,据此判断A;由图象得当x=-1时,函数取得最小值,ymin=a-b-2,进而判断B;当x=1时,y=a+b-2<0,结合b=2a可判断C;由图象可得直线l与抛物线的两个交点分别在y轴的两侧,据此判断D.
10.【答案】D
【解析】【解答】解:∵四边形是矩形,,
∴,
∴,
∵,
∴,
∴,故①正确;
②∵,
∴,,
∴,
∵,
∴,
∴,
∴为的角平分线,故②正确;
③连接,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,,
∴,
∵,
∴,
∴,
∴,,
∴, ,
∴,
∴,
∵,
∴,
∴,
∴,故③正确;
∵平分,
∴,
∴,
设,
∴,
∵,
∴,
解得:,
∴矩形的面积为:,故④正确;
故答案为:D.
【分析】分类讨论,利用矩形的性质,全等三角形的判定与性质,勾股定理计算求解即可。
11.【答案】
【解析】【解答】解:由 ,可设a=2k,b=3k,(k≠0),
故: ,
故答案: .
【分析】根据比例的性质,由 ,可设a=2k,b=3k,(k≠0),然后将a,b的值代入代数式,按整式的混合运算法则即可算出答案。
12.【答案】-2
【解析】【解答】解:∵函数y=是二次函数,
∴2﹣a≠0, ,
∴a≠2,
∴
故答案为:.
【分析】形如“y=ax2+bx+c(a、b、c都是常数,且a≠0)”的函数就是二次函数,据此可得2-a≠0且a2-2=2,求解即可.
13.【答案】6
【解析】【解答】解:在矩形纸片ABCD中,∠B =∠D= 90°,AD=BC,
由折叠性质得AF=AD=BC,∠AFE=∠D=∠B = 90°,
∴∠BAF+∠AFB = 90°,∠EFC+∠AFB=90°,
∴∠BAF=∠EFC,
在Rt△ABF中,
,
∵CF=4,
则,
解得BF= 6;
故答案为:6.
【分析】根据折叠性质和矩形性质得到AF=AD=BC,∠AFE=∠D=∠B=90°,根据等角的余角相等得到∠BAF=∠EFC,再根据,求解即可.
14.【答案】2
【解析】【解答】设点A的坐标为,设AC与x轴的交点为E,过点B作BF⊥x轴,垂足为F,如图,
∵点C在函数的图象上,且AC⊥x轴,
∴C的坐标为,
∴EC=k,
∵BF⊥x轴,CE⊥x轴,
∴ ,
∴ ,
又∵,
∴ ,
∴,
即,
∴点B的纵坐标为,代入反比例函数解析式:,
当时,,
∴B点的横坐标是2,
故答案为:2.
【分析】设点A的坐标为,设AC与x轴的交点为E,过点B作BF⊥x轴,垂足为F,先证明可得,再结合可得,求出,再将点B的坐标代入可得,求出k的值,即可得到点B的横坐标。
15.【答案】
【解析】【解答】解:过点A作AM⊥BC于点M,
∵AB=AC=5,BC=8,
∴BM=CM=4,
∴AM==3.
∵BD=AB=5,
∴DM=BD-BM=AB-BM=5-4=1,
∴AD=,CD=CM-DM=4-1=3.
∵AB=AC,
∴∠B=∠C.
∵∠ADE=∠B,
∴∠ADE=∠C.
∵BD=AB,
∴∠BAD=∠BDA.
∵∠BAD=∠ADE+∠E,∠BDA=∠C+∠DAC,
∴∠E=∠DAC,
∴△ADE∽△DCA,
∴,
∴DE=.
∵∠ADE=∠C,∠DAF=∠CAD,
∴△ADF∽△ACD,
∴,
∴DF=,
∴EF=DE-DF=-=.
故答案为:.
【分析】过点A作AM⊥BC于点M,由等腰三角形的性质可得BM=CM=4,利用勾股定理可得AM,然后求出DM、AD,根据等腰三角形的性质可得∠B=∠C,结合∠ADE=∠B可得∠ADE=∠C,利用两角对应相等的两个三角形相似可得△ADE∽△DCA、△ADF∽△ACD,由相似三角形的性质可得DE、DF,然后根据EF=DE-DF进行计算.
16.【答案】解:原式
【解析】【分析】先代入特殊锐角三角函数值,同时根据负整数指数幂的性质、0指数幂的性质及绝对值的性质分别化简,然后再计算二次根式的乘法,最后计算有理数的加减法即可得出答案.
17.【答案】(1)240;36°
(2)解:最喜欢D活动的人数占总调查人数:,
∴最喜欢C活动的人数占总调查人数:1-35%-25%-10%=30%,
∴1000名学生中最喜欢C活动的人数约有:人.
(3)树状图如下:
恰好选到甲和丁同学有2种情况,总的情况有12种,
∴恰好选到甲和丁同学的概率为.
18.【答案】解:过点C作CM⊥AB于M.则四边形MEDC是矩形,
∴ME=DC=3.CM=ED,
在Rt△AEF中,∠AFE=60°,设EF=x,则AF=2x,AE= x,
在Rt△FCD中,CD=3,∠CFD=30°,
∴DF=3 ,
在Rt△AMC中,∠ACM=45°,
∴∠MAC=∠ACM=45°,
∴MA=MC,
∵ED=CM,
∴AM=ED,
∵AM=AE﹣ME,ED=EF+DF,
∴ x﹣3=x+3 ,
∴x=6+3 ,
∴AE= (6+3 )=6 +9,
∴AB=AE﹣BE=9+6 ﹣1≈18.4米.
答:旗杆AB的高度约为18.4米.
【解析】【分析】过点C作CM⊥AB于M.则四边形MEDC是矩形,设EF=x,根据AM=DE,列出方程即可解决问题.
19.【答案】(1) 解:函数图象如图所示:
(2)增大;上;1;(0,1)
(3) 解:∵x1+x2=0,
∴x1=﹣x2,
∴A(x1,y1),B(x2,y2)关于(0,1)对称,
∴y1+y2=2,
∴y1+y2+3=5
【解析】【解答】解:(2)①当x<0时,y随x的增大而增大;
②y= 的图象是由y=﹣ 的图象向上平移1个单位而得到;
③图象关于点(0,1)中心对称.(填点的坐标)
故答案为增大,上,1,(0,1)
【分析】(1)利用描点法,画出函数的图象。
(2)①观察函数图象,进行分析可知x<0时,y随x的变化情况;②观察函数的图象,可知可得到两图像的平移规律;③然后就可得到y= 的图像是关于(0,1)对称。
(3)由x1+x2=0,可得到x1=﹣x2,再由A(x1,y1),B(x2,y2)关于(0,1)对称,就可求出y1+y2,然后整体代入可求解。
20.【答案】(1)证明:Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=45°,
∴45°+∠EDC=45°+∠BAD.
∴∠EDC=∠BAD.
∴△ABD∽△DCE.
(2)解:讨论:①若AD=AE时,∠DAE=90°,此时D点与点B重合,不合题意.
②若AD=DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,
于是AB=AC=2,BC=2,AE=AC﹣EC=2﹣BD=2﹣(2﹣2)=4﹣2
③若AE=DE,此时∠DAE=∠ADE=45°,
如下图所示易知AD⊥BC,DE⊥AC,且AD=DC.由等腰三角形的三线合一可知:AE=CE=AC=1.
【解析】【分析】(1)首先根据等腰直角三角形的两个底角都是45°,得到一对对应角相等;再根据三角形的外角的性质得到∠ADE+∠EDC=∠B+∠BAD,从而证明∠EDC=∠BAD,根据两个角对应相等,得到两个三角形相似;
(2)根据等腰三角形的定义,此题要分三种情况进行分析讨论.根据等腰三角形的性质进行计算.
21.【答案】(1)解:,
该抛物线的顶点为;
,
该抛物线的顶点坐标为.
设经过点和点的直线的解析式为,
,
解得:.
.
它们的根函数为直线.
(2)解:,
该抛物线的顶点坐标为,
设顶点在直线上,
.
解得:,
顶点在直线上,
满足二次函数的所有二次函数的根函数为.
二次函数与直线交于点,
.
.
,
点的纵坐标当时,由最小值为.
点到轴的最小距离为,此时.
【解析】【分析】(1)首先根据配方法分别求出两条抛物线的顶点坐标,然后根据根函数的定义,设出直线解析式,将两个顶点坐标代入所设的直线解析式中求出即可.
(2)①首先根据配方法求出二次函数的顶点坐标,然后根据根函数的定义,代入定点左边即可求出根函数的解析式.
②先根据二次函数与直线x=-3交于点P,求出点P的坐标,然后算出点P到x轴的距离,对其配方即可求出最小值.
22.【答案】(1)解:,,理由如下:
如图,延长交于点,
为等腰直角三角形,,
,
为等腰直角三角形,,
,,
又,
,
,
在中,点为斜边的中点,
,
,
设,则,
,
,
在,点为斜边的中点,
,
,
,
,
;
(2)解:结论,,仍然成立,理由如下:
如图,取的中点,连接,,延长分别交,于点,,
点,分别是,的中点,
,
,
,
在等腰中,点是的中点,
,,
,
点,分别是,的中点,
,
,
,
,
,
,
,即,
,
,
在和中,
,,
,即.
综上:,;
(3);
【解析】【解答】解:(3)①如图,取的中点,连接,,延长分别交,于点,
∵,,
∴,
∵,
∴,
∴,
∴,
点,分别是,的中点,
,,
,
在等腰中,点是的中点,,
,,,
∴,
∴,即,
,
点,分别是,的中点,
,
,
,
,
,
,
,
∴;
故答案为:
②∵,,
∴点D在以点B为圆心,长为半径的圆上运动,
∴当时,最大,
过点E作,
∴,
∴四边形为矩形,
∴,
在中,,
在中,,,
∴,
∴,
在中, ,
由①得:,
.
【分析】(1),,理由:延长交于点,根据SAS证明△DBC≌△EBC,可得CD=CE,根据直角三角形斜边中线的性质可得AF=CD=CE, 设,则, 由全等三角形的性质可得,再根据直角三角形斜边中线的性质可得AF=CF,利用等腰三角形的性质及三角形内角和求出∠FPC=90°,继而得解;
(2)仍然成立,理由:取的中点,连接,,延长分别交,于点,, 根据三角形中位线定理及等腰直角三角形可得 , 再证明, 可得 ,,继而得解;
(3)①取的中点,连接,,延长分别交,于点,,根据等腰三角形及直角三角形的性质可得,再证,利用相似三角形的性质即可求解;②判断出点D在以点B为圆心,长为半径的圆上运动,则当时,最大,过点E作,则四边形为矩形,可得,由勾股定理求出CD,从而得出CH,在中,由勾股定理求出CE,继而得解.
1 / 1
同课章节目录
